Cho một tấm nhôm hình vuông cạnh  6 cm. Người ta muốn cắt một hình thang như hình vẽ. Tìm tổng x + y  để dịnh tích hình thang EFGH đạt giá trị nhỏ nhất.

Câu hỏi:

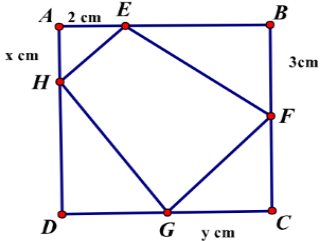
Cho một tấm nhôm hình vuông cạnh  6 cm. Người ta muốn cắt một hình thang như hình vẽ. Tìm tổng x + y  để dịnh tích hình thang EFGH đạt giá trị nhỏ nhất.

A. $2+\sqrt{3}$

B. $3\sqrt{2}$

C. $2\sqrt{2}$

D. Tất cả sai

Đáp án chính xác

Trả lời:

Ta có S_EFGH nhỏ nhất  $\leftrightarrow S = S_{AEH} + S_{CGF} +S_{DGH}$ lớn nhất
Tính được 2S= 2x+ 3y+ (6-x) (6-y) = xy-4x-3y+36          (1)
Mặt khác ∆ AEH đồng dạng  ∆CGF nên  $\frac{AE}{CG} = \frac{AH}{CF} \Rightarrow xy = 6$
Từ (1) và (2) suy ra  2S = $42 – (4x –\frac{18}{x})$
Ta có 2S  lớn nhất khi và chỉ khi  $4x – \frac{18}{x}$nhỏ nhất.
Biểu thức nhỏ nhất  $4x – \frac{18}{x}$ nhỏ nhất  $\leftrightarrow 4x = \frac{18}{x} \Rightarrow x = \frac{3\sqrt{2}}{2} \Rightarrow y = 2\sqrt{2}$
Vậy  x+y = $\frac{3\sqrt{2}}{2}+2\sqrt{2}$
Chọn D.

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Cho hàm số y = f(x) = ax +bcx + d ( a,b,c,d ∈ ℝ,  -dc ≠0) đồ thị hàm số y= f’(x) như hình vẽ. Biết đồ thị hàm số y= f(x)  cắt trục tung tại điểm có tung độ bằng 3. Tìm phương trình tiếp tuyến của (C) tại giao điểm của (C) với trục hoành ?  
   
   

   Câu hỏi:
   

   Cho hàm số y = f(x) = $\frac{ax +b}{cx + d}$ ( a,b,c,d $\in \mathrm{ℝ}$,  $\frac{–d}{c}$ $\ne$0) đồ thị hàm số y= f’(x) như hình vẽ.
   
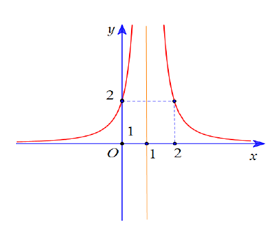
   Biết đồ thị hàm số y= f(x)  cắt trục tung tại điểm có tung độ bằng 3. Tìm phương trình tiếp tuyến của (C) tại giao điểm của (C) với trục hoành ?
    

   A. y = $\frac{x–3}{x+1}$

   B. y = $\frac{x+3}{x–1}$

   C. y = $\frac{x+ 3}{x+1}$

   D. y = $\frac{x – 3}{x –1}$

   Đáp án chính xác

   Trả lời:

   + Ta có $y^{‘} = f^{‘}\left(x\right)$ = $\frac{ad – bc}{{(cx + d)}^2}$ . Từ đồ thị hàm số y= f’(x)  ta thấy:
   Đồ thị hàm số y= f’(x)  có tiệm cận đứng x=1 nên –d/c= 1 hay  c= -d
   Đồ thị hàm số y= f’(x )  đi qua điểm (2;2)
   $\Rightarrow \frac{ad – bc}{{(2c + d)}^2} = 2 \leftrightarrow ad – bc = 2$ $(2c+d{)}^2$
   Đồ thị hàm số y= f’(x)  đi qua điểm (0;2)
   $\Rightarrow \frac{ad – bc}{d^2} = 2 \leftrightarrow ad – bc = 2d^2$
   Đồ thị hàm số y=f(x)  đi qua điểm (0;3) nên b/d= 3 hay b= 3d
   Giải hệ  gồm 4 pt này ta được a=c= -d và b= 3d  .
    Ta chọn a=c= 1 ; b= -3 ; d= -1  
   $\Rightarrow y = \frac{x – 3}{x –1 }$
   Chọn  D.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Trong các đồ thị hàm số sau, đồ thị nào là đồ thị của hàm số y = xx – 1 ?
   
   

   Câu hỏi:
   

   Trong các đồ thị hàm số sau, đồ thị nào là đồ thị của hàm số $y = \frac{x}{\left|x – 1\right|}$ ?

   A. 

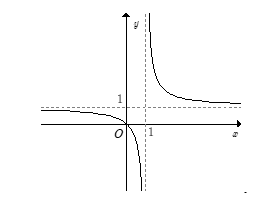
   B.

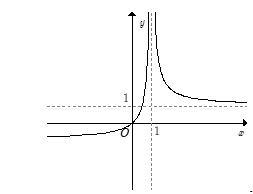
   Đáp án chính xác

   C.

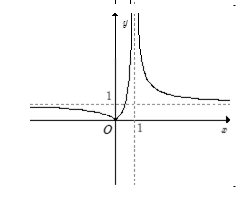
   D. 

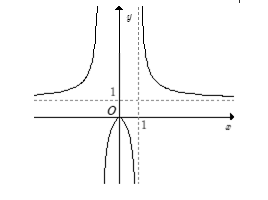
   Trả lời:

   Ta có  y = $\frac{x}{\left|x – 1\right|} = \left\{\begin{array}{l}\frac{x}{x–1} khi x > 1\\ –\frac{x}{x–1} khi x <\hspace{0.17em}1\end{array}\right.$
   Do đó đồ thị hàm số  $y = \frac{x}{\left|x –1 \right|}$ được suy từ đồ thị hàm số  $y = \frac{x}{x –1 }$bằng cách:
   ● Giữ nguyên phần đồ thị hàm số  phía bên phải đường thẳng x = 1.
   ● Phần đồ thị hàm số 
   $y = \frac{x}{x–1}$  
   phía bên trái đường thẳng x= 1 thì lấy đối xứng qua trục hoành.
   Hợp hai phần đồ thị ở trên ta được toàn bộ đồ thị hàm số  y = $\frac{x}{\left|x –1\right|}$
   Chọn B.
    

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Hàm số y= 2×3-9×2+ 12x  có đồ thị như hình vẽ bên. Tìm tất cả các giá trị của tham số m  để phương trình  2×3-9×2  + 12x + m = 0 có sáu nghiệm phân biệt.
   
   

   Câu hỏi:
   

   Hàm số y= 2x³-9x²+ 12x  có đồ thị như hình vẽ bên. Tìm tất cả các giá trị của tham số m  để phương trình  $2{\left|x\right|}^3–9x^{2 } + 12\left|x\right| + m = 0$ có sáu nghiệm phân biệt.
   

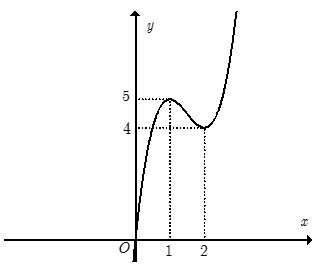
   A.m< – 5

   B. -5< m<- 4

   Đáp án chính xác

   C. 4< m< 5

   D.m> -4

   Trả lời:

   +Trước tiên từ đồ thị hàm số y= 2x³– 9x²+12x , ta suy ra đồ thị hàm số  y= 2${\left|x\right|}^3 – 9x^2 + 12\left|x\right|$  như hình dưới đây:
   
   + Phương trình $2{\left|x\right|}^3 – 9x^2 + 12\left|x\right| + m = 0$ và đường thẳng y= -m
   + Dựa vào đồ thị hàm số   y = $2{\left|x\right|}^3 – 9x^2 + 12\left|x\right|$, yêu cầu bài toán trở thành:
   4< -m< 5 hay -5<m< -4.
   Chọn B.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
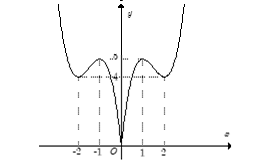
4. Cho hàm số y= f(x)  xác định trên R  và có đồ thị như hình bên. Hỏi với những giá trị nào của tham số thực m thì phương trình  f(x) = m có đúng hai nghiệm phân biệt.
   
   

   Câu hỏi:
   

   Cho hàm số y= f(x)  xác định trên R  và có đồ thị như hình bên. Hỏi với những giá trị nào của tham số thực m thì phương trình  $\left|f\left(x\right)\right| = m$ có đúng hai nghiệm phân biệt.
   

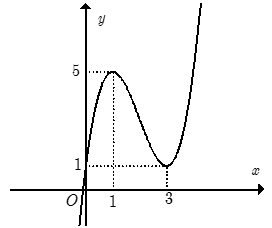
   A.0< m< 1 .

   B. m> 5.

   C.m= 1; m= 5

   D.0< m< 1; m> 5

   Đáp án chính xác

   Trả lời:

   + Ta có y = $\left|f\left(x\right)\right| = \left\{\begin{array}{l}f\left(x\right) , f\left(x\right) \ge 0\\ –f\left(x\right), f\left(x\right) <0\end{array}\right.$. Từ đó suy ra cách vẽ  đồ thị hàm số (C) như sau:
   – Giữ nguyên đồ thị y= f (x)  phía trên trục hoành.
   – Lấy đối xứng phần đồ thị y= f(x)  phía dưới trục hoành qua trục hoành ( bỏ phần dưới ).
   Kết hợp hai phần ta được đồ thị hàm số  y = $\left|f\left(x\right)\right|$ như hình vẽ.
   
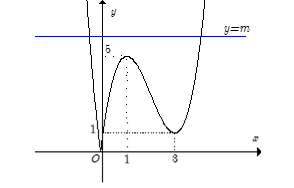
   Phương trình $\left|f\left(x\right)\right| = m$  là phương trình hoành độ giao điểm của đồ thị hàm số y = $\left|f\left(x\right)\right|$ và đường thẳng
   y= m  (cùng phương với trục hoành).
   Dựa vào đồ thị, ta có ycbt
    
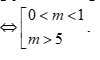
   Chọn D.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
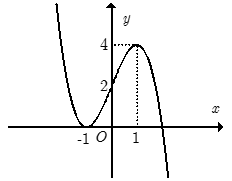
5. Cho hàm số y= f(x)  xác định trên   R  và có đồ thị như hình bên. Tìm tất cả các giá trị thực của tham số m để phương trình 2f(x) – m = 0 có đúng bốn nghiệm phân biệt. 
   
   

   Câu hỏi:
   

   Cho hàm số y= f(x)  xác định trên   R  và có đồ thị như hình bên. Tìm tất cả các giá trị thực của tham số m để phương trình
   2$\left|f\left(x\right)\right|$ – m = 0 có đúng bốn nghiệm phân biệt. 
   

   A. 0< m< 8

   Đáp án chính xác

   B.m> 4

   C.m< 0 ; m> 8

   D. -2< m< 4

   Trả lời:

   + Trước tiên từ đồ thị hàm số y = f( x) , ta suy ra đồ thị hàm số y = |f(x)| như hình dưới đây: 
   
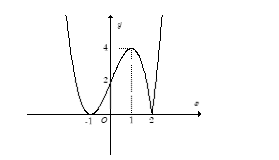
   Phương trình 2|f(x)| – m = 0 hay |f(x)| = m/2 là phương trình hoành độ giao điểm của đồ thị hàm số y = |f(x)| và đường thẳng y = m/2.
   Dựa vào đồ thị hàm số  y = |f(x)|, ta có ycbt trở thành:
   
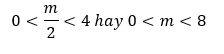
   Chọn A.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====