Cho lăng trụ ABCD. A’B’C’D’ có đáy ABCD là hình vuông cạnh a, cạnh bên AA’=a . hình chiếu vuông góc của A’ trên mặt phẳng (ABCD) trùng với trung điểm H của AB. Tính theo a thể tích V của khối lăng trụ đã cho

Câu hỏi:

Cho lăng trụ ABCD. A’B’C’D’ có đáy ABCD là hình vuông cạnh a, cạnh bên AA’=a . hình chiếu vuông góc của A’ trên mặt phẳng (ABCD) trùng với trung điểm H của AB. Tính theo a thể tích V của khối lăng trụ đã cho

A.   $V=\frac{a^3\sqrt{3}}{6}.$        

B. $V=\frac{a^3\sqrt{3}}{2}.$

Đáp án chính xác

C. $V=a^3.$

D. $V=\frac{a^3}{3}.$

Trả lời:

Đáp án B.

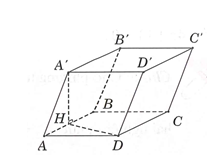
Theo giả thiết, ta có $A^{‘}H\perp AB.$
Tam giác vuông $A^{‘}HA,$  có $A^{‘}H=\sqrt{A^{‘}{A}^2-A{H}^2}=\frac{a\sqrt{3}}{2}.$
Diện tích hình vuông $S_{ABCD}=a^2$  (đvdt).
Thể tích khối lăng trụ $ABCD.A^{‘}{B}^{‘}{C}^{‘}{D}^{‘}$  là:
$V_{ABCD.A^{‘}{B}^{‘}{C}^{‘}{D}^{‘}}=S_{ABC}.A^{‘}H=\frac{a^3\sqrt{3}}{2}$(đvtt)

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Cho mặt cầu (S) có diện tích bằng 4π.  Thể tích khối cầu (S) bằng:
   
   

   Câu hỏi:
   

   Cho mặt cầu (S) có diện tích bằng $4\pi .$  Thể tích khối cầu (S) bằng:

   A. $16\pi .$

   B. $32\pi .$

   C. $\frac{4\pi }{3}.$

   Đáp án chính xác

   D. $\frac{16\pi }{3}.$

   Trả lời:

   Đáp án C.
   Diện tích mặt cầu (S) là: $4\pi R^2=4\pi \Rightarrow R=1.$
   Do dó thể tích khối cầu (S) là: $V=\frac{4}{3}\pi .R^3=\frac{4}{3}\pi$ (đvtt).

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Hệ thức liên hệ giữa giá trị cực đại và giá trị cực tiểu của hàm số y=x3−2x  là
   
   

   Câu hỏi:
   

   Hệ thức liên hệ giữa giá trị cực đại và giá trị cực tiểu của hàm số $y=x^3-2x$  là

   A. $y_{CT}+y_{CD}=0.$

   Đáp án chính xác

   B. $y_{CD}=y_{CT}.$

   C. $2y_{CD}=3y_{CT}.$

   D. $y_{CD}=2y_{CT}.$

   Trả lời:

   Đáp án A.
   TXĐ: $D=ℝ.$
   Ta có $y^{‘}=3x^2-2=0\iff x=\pm \sqrt{\frac{2}{3}}\Rightarrow x_{CT}=-x_{CD}.$
   Mà hàm số đã cho là hàm số lẻ nên ta suy ra $y_{CT}=-y_{CD}$  hay $y_{CT}+y_{CD}=0.$

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Trong không gian với hệ tọa độ Oxyz, cho hai vectơ a→=2;−3;1  và b→=−1;4;−2.  Giá trị của biểu thức a→.b→  bằng
   
   

   Câu hỏi:
   

   Trong không gian với hệ tọa độ Oxyz, cho hai vectơ $\overrightarrow{a}=\left(2;-3;1\right)$  và $\overrightarrow{b}=\left(-1;4;-2\right).$  Giá trị của biểu thức $\overrightarrow{a}.\overrightarrow{b}$  bằng

   A. -16

   Đáp án chính xác

   B.-4

   C. 4.

   D. 16.

   Trả lời:

   Đáp án A.
   Ta có: $\overrightarrow{a}.\overrightarrow{b}=2.\left(-1\right)+\left(-3\right).4+1.\left(-2\right)=-16.$

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Cho hàm số y=x4−2×2.  Mệnh đề nào sau đây đúng?
   
   

   Câu hỏi:
   

   Cho hàm số $y=x^4-2x^2.$  Mệnh đề nào sau đây đúng?

   A. Hàm số đồng biến trên khoảng $\left(-\infty ;-2\right).$

   B. Hàm số nghịch biến trên khoảng   $\left(-\infty ;-2\right).$      

   Đáp án chính xác

   C. Hàm số đồng biến trên khoảng  $\left(-1;1\right).$  

   D. Hàm số nghịch biến trên khoảng $\left(-1;1\right).$

   Trả lời:

   Đáp án B.
   TXĐ: $D=ℝ.$
   Ta có $y^{‘}=4x^3-4x=0\iff \left[\begin{array}{l}x=0\\ x=\pm 1\end{array}\right..$
   Bảng xét dấu  như sau:
   
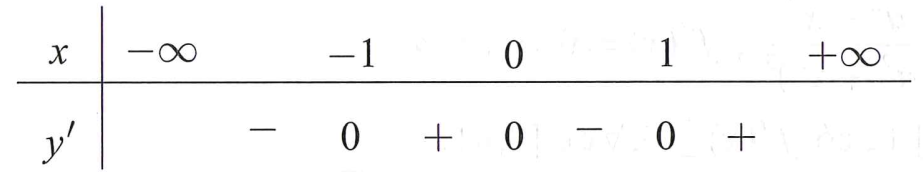
   Dựa vào bảng xét dấu, suy ra hàm số đã cho nghịch biến trên các khoảng  $\left(-\infty ;-1\right)$ và $\left(0;1\right);$  nên nghịch biến trên khoảng $\left(-\infty ;-2\right).$

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Biểu thức P=x.x2.x53=xα  (với x>0  ), giá trị của  là
   
   

   Câu hỏi:
   

   Biểu thức $P=x.x^2.\sqrt{x}53=x^{\alpha }$  (với $x>0$  ), giá trị của  là

   A. $\frac{1}{2}.$

   Đáp án chính xác

   B. $\frac{5}{2}.$

   C. $\frac{9}{2}.$

   D. $\frac{3}{2}.$

   Trả lời:

   Đáp án A.
   Với x > 0 ta có: $P=x.x^2.\sqrt{x}53=x.x^2.x^{\frac{1}{2}}53=x.x^{\frac{5}{2}}53=x.x^{\frac{1}{2}}3=x^{\frac{3}{2}}3=x^{\frac{1}{2}}=x^{\alpha }$
   Vậy $\alpha =\frac{1}{2}.$

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====