Câu hỏi:
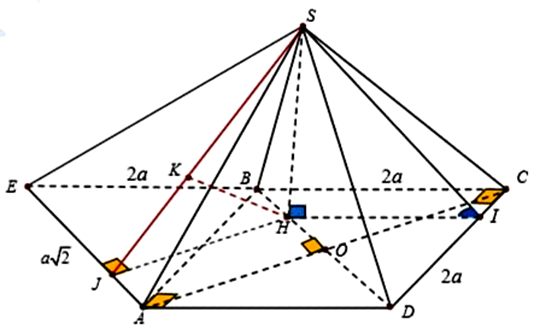
Cho khối chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a. Hình chiếu vuông góc của S trên mặt phẳng \(\left( {ABCD} \right)\) là điểm H thuộc đoạn BD sao cho \(HD = 3HB\). Biết gọc giữa mặt \(\left( {SCD} \right)\) và mặt phẳng đáy bằng \(45^\circ .\) Khoảng cách giữa hai đường thẳng SA và BD là
A. \(\frac{{2a\sqrt {38} }}{{17}}.\)
B. \(\frac{{2a\sqrt {13} }}{3}.\)
C. \(\frac{{2a\sqrt {51} }}{{13}}.\)
D. \(\frac{{3a\sqrt {34} }}{{17}}.\)
Đáp án chính xác
Trả lời:
Đáp án D
Kẻ \(HI{\rm{ // BC}}\) cắt CD tại I ta có: \(\left\{ \begin{array}{l}C{\rm{D}} \bot {\rm{HI}}\\{\rm{CD}} \bot {\rm{S}}I\end{array} \right.\).
Suy ra góc giữa mặt phẳng \(\left( {SC{\rm{D}}} \right)\) và mặt phẳng đáy là góc \(\widehat {SIH} = 45^\circ \).
Dựng hình bình hành ADBE.
Ta có \(B{\rm{D // }}\left( {SA{\rm{E}}} \right) \Rightarrow d\left( {SA,B{\rm{D}}} \right) = d\left( {B{\rm{D}},(SA{\rm{E}})} \right) = d\left( {B,(SA{\rm{E}})} \right) = d\left( {H,(SA{\rm{E}})} \right)\).
Kẻ \(HJ \bot A{\rm{E}}\) vuông góc tại J ta có \(A{\rm{E}} \bot \left( {SHJ} \right) \Rightarrow \left( {SA{\rm{E}}} \right) \bot \left( {SHJ} \right)\) theo giao tuyến SJ.
Kẻ \(HK \bot {\rm{S}}J\) vuông góc tại K ta có \(HK \bot \left( {SA{\rm{E}}} \right) \Rightarrow HK = d\left( {H,(SA{\rm{E}})} \right)\).
Ta có \(HK = \frac{{HJ.H{\rm{S}}}}{{SJ}} = \frac{{HJ.H{\rm{S}}}}{{\sqrt {H{J^2} + H{{\rm{S}}^2}} }}\).
Với \(HJ = AO = a\sqrt 2 ,{\rm{ }}HI = \frac{3}{4}BC = \frac{{3a}}{2}\).
Và \(H{\rm{S}} = HI = \frac{{3{\rm{a}}}}{2}\).
Vậy \(HK = \frac{{a\sqrt 2 .\frac{{3{\rm{a}}}}{2}}}{{\sqrt {2{{\rm{a}}^2} + \frac{{9{{\rm{a}}^2}}}{4}} }} = \frac{{3{\rm{a}}\sqrt {34} }}{{17}}\).
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau
Mệnh đề nào dưới đây sai?
Câu hỏi:
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau
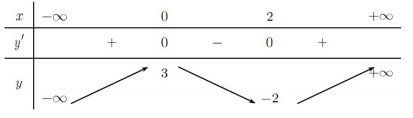
Mệnh đề nào dưới đây sai?A. Hàm số đồng biến trên khoảng \(\left( {2; + \infty } \right).\)
B. Hàm số nghịch biến trên khoảng \(\left( { – \infty ;2} \right).\)
Đáp án chính xác
C. Hàm số nghịch biến trên khoảng \(\left( {0;2} \right).\)
D. Hàm số đồng biến trên khoảng \(\left( { – \infty ;0} \right).\)
Trả lời:
Đáp án B
Từ bảng biến thiên ta có:
Hàm số nghịch biến trên khoảng \(\left( {0;2} \right)\).
Hàm số đồng biến trên khoảng \(\left( { – \infty ;0} \right)\) và \(\left( {2; + \infty } \right)\).
Do đó B là mệnh đề sai.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Trong không gian Oxyz, đường thẳng \(d:\left\{ {\begin{array}{*{20}{l}}{x = 2 – t}\\{y = 1 + 2t}\\{z = 3 + t}\end{array}} \right.\) có một vectơ chỉ phương là
Câu hỏi:
Trong không gian Oxyz, đường thẳng \(d:\left\{ {\begin{array}{*{20}{l}}{x = 2 – t}\\{y = 1 + 2t}\\{z = 3 + t}\end{array}} \right.\) có một vectơ chỉ phương là
A. \(\overrightarrow {{u_3}} = \left( {2;1;3} \right).\)
B. \(\overrightarrow {{u_1}} = \left( { – 1;2;3} \right).\)
C. \(\overrightarrow {{u_2}} = \left( {2;1;1} \right).\)
D. \(\overrightarrow {{u_4}} = \left( { – 1;2;1} \right).\)
Đáp án chính xác
Trả lời:
Đáp án D
Đường thẳng d có một VTCP là \(\overrightarrow u = \left( { – 1;2;1} \right)\).====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Hình nón có bán kính đáy, chiều cao, đường sinh lần lượt là \(r,h,l\). Diện tích xung quanh của hình nón là:
Câu hỏi:
Hình nón có bán kính đáy, chiều cao, đường sinh lần lượt là \(r,h,l\). Diện tích xung quanh của hình nón là:
A. \(S = \pi rh.\)
B. \(S = \pi {r^2}.\)
C. \(S = \pi hl.\)
D. \(S = \pi rl.\)
Đáp án chính xác
Trả lời:
Đáp án D
Diện tích xung quanh của hình nón bằng một nửa tích của độ dài đường tròn đáy và độ dài đường sinh: \(S = \pi r\ell \).====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Số phức liên hợp của \(z = 4 + 3i\) là
Câu hỏi:
Số phức liên hợp của \(z = 4 + 3i\) là
A. \(\bar z = – 3 + 4i.\)
B. \(\bar z = 4 – 3i.\)
Đáp án chính xác
C. \(\bar z = 3 + 4i.\)
D. \(\bar z = 3 – 4i.\)
Trả lời:
Đáp án B
Số phức liên hợp của \(z = 4 + 3i\) là \(\overline z = 4 – 3i\).====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho \(a > 0;b > 0\). Tìm đẳng thức sai.
Câu hỏi:
Cho \(a > 0;b > 0\). Tìm đẳng thức sai.
A. \({\log _2}{\left( {ab} \right)^2} = 2{\log _2}\left( {ab} \right)\)
B. \({\log _2}a + {\log _2}b = {\log _2}\left( {ab} \right)\)
C. \({\log _2}a – {\log _2}b = {\log _2}\frac{a}{b}\)
D. \({\log _2}a + {\log _2}b = {\log _2}\left( {a + b} \right)\)
Đáp án chính xác
Trả lời:
Đáp án D
Sử dụng các công thức:
\({\log _a}x + {\log _a}y = {\log _a}\left( {xy} \right)\)
\({\log _a}x – {\log _a}y = {\log _a}\frac{x}{y}\)
\({\log _{{a^n}}}{b^m} = \frac{m}{n}{\log _a}b\)
\(\left( {0 < a \ne 1;x,y,b > 0} \right)\).
Dựa vào các đáp án ta thấy đáp án D sai.====== **** mời các bạn xem câu tiếp bên dưới **** =====