Cho hình trụ có diện tích toàn phần là 6π và có thiết diện cắt bởi mặt phẳng qua trục là hình vuông. Thể tích khối trụ đã cho bằng

Câu hỏi:

Cho hình trụ có diện tích toàn phần là 6π và có thiết diện cắt bởi mặt phẳng qua trục là hình vuông. Thể tích khối trụ đã cho bằng

A. 4π                         

B. 8π                         

C. 6π                         

D. 2π

Đáp án chính xác

Trả lời:

Đáp án D
Kí hiệu h, r lần lượt là chiều cao và bán kính đáy của hình trụ.
Theo giả thiết ta có: \(\left\{ \begin{array}{l}6\pi = 2\pi rh + 2\pi {r^2}\\h = 2{\rm{r}}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}6 = 4{{\rm{r}}^2} + 2{r^2}\\h = 2{\rm{r}}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}h = 2\\r = 1\end{array} \right.\).
Mặt khác, \(V = \pi {r^2}h = \pi {.2.1^2} = 2\pi \).

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Cho 10 điểm phân biệt trong đó không có 3 điểm nào thẳng hàng. Hỏi có bao nhiêu tam giác mà ba đỉnh của nó được chọn từ 10 điểm trên?
   
   

   Câu hỏi:
   

   Cho 10 điểm phân biệt trong đó không có 3 điểm nào thẳng hàng. Hỏi có bao nhiêu tam giác mà ba đỉnh của nó được chọn từ 10 điểm trên?

   A. \(C_{10}^3\)         

   B. \(A_{10}^3\)           

   C. \(C_{10}^3 – 10\) 

   Đáp án chính xác

   D. \({10^3}\)

   Trả lời:

   Đáp án A
   Chọn 3 điểm từ 10 điểm phân biệt trong đó không có 3 điểm nào thẳng hàng ta được một tam giác suy ra có \(C_{10}^3\) tam giác dược tạo thành.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Trong không gian với hệ tọa độ Oxyz cho điểm \(A\left( {1; – 1;2} \right)\) và mặt phẳng \(\left( P \right):2{\rm{x}} – y + z + 1 = 0\). Mặt phẳng \(\left( Q \right)\) đi qua điểm A và song song với \(\left( P \right)\). Phương trình mặt phẳng \(\left( Q \right)\) là
   
   

   Câu hỏi:
   

   Trong không gian với hệ tọa độ Oxyz cho điểm \(A\left( {1; – 1;2} \right)\) và mặt phẳng \(\left( P \right):2{\rm{x}} – y + z + 1 = 0\). Mặt phẳng \(\left( Q \right)\) đi qua điểm A và song song với \(\left( P \right)\). Phương trình mặt phẳng \(\left( Q \right)\) là

   A. \(2{\rm{x}} – y + z – 5 = 0\)                     

   Đáp án chính xác

   B. \(2{\rm{x}} – y + z = 0\)    

   C. \(x + y + z – 2 = 0\)                             

   D. \(2{\rm{x}} + y – z + 1 = 0\)

   Trả lời:

   Đáp án A
   Do \(\left( Q \right)\) song song với \(\left( P \right)\) nên phương trình của \(\left( Q \right)\) có dạng \(2{\rm{x}} – y + z + a = 0\) với \(a \ne 1\).
   Do \(\left( Q \right)\) đi qua điểm A nên \(2.1 + 1 + 2 + a = 0 \Leftrightarrow a = – 5\).
   Vậy phương trình \(\left( Q \right):2{\rm{x}} – y + z – 5 = 0\).

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Số nghiệm nguyên của bất phương trình \({\log _{\frac{1}{2}}}\left( {x – 3} \right) \ge {\log _{\frac{1}{2}}}4\) là
   
   

   Câu hỏi:
   

   Số nghiệm nguyên của bất phương trình \({\log _{\frac{1}{2}}}\left( {x – 3} \right) \ge {\log _{\frac{1}{2}}}4\) là

   A. 5                           

   B. 6                           

   C. 3                           

   D. 4

   Đáp án chính xác

   Trả lời:

   Đáp án D
   Ta có: BPT . Do đó có 4 giá trị nguyên thỏa mãn.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, cạnh bên bằng \(\sqrt 2 a\). Độ lớn của góc giữa đường thẳng SA và mặt phẳng đáy bằng
   
   

   Câu hỏi:
   

   Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, cạnh bên bằng \(\sqrt 2 a\). Độ lớn của góc giữa đường thẳng SA và mặt phẳng đáy bằng

   A. \(45^\circ \)            

   B. \(75^\circ \)            

   C. \(30^\circ \)            

   D. \(60^\circ \)

   Đáp án chính xác

   Trả lời:

   Đáp án D
   
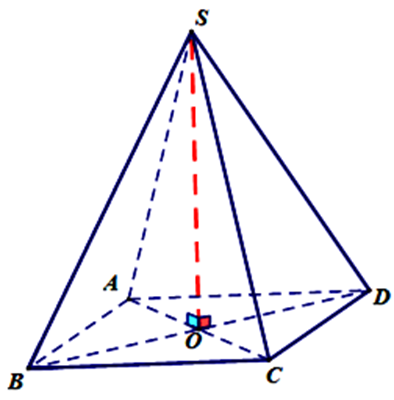
   Gọi O là tâm hình vuông.
   Suy ra AO là hình chiếu vuông góc của SA lên mặt phẳng \(\left( {ABC{\rm{D}}} \right)\).
   Vậy góc giữa đường thẳng SA và mặt phẳng \(\left( {ABC{\rm{D}}} \right)\) là \(\widehat {SAO}\).
   Tam giác SAO vuông tại O có
   \(\cos \widehat {SAO} = \frac{{AO}}{{SA}} = \frac{{\frac{{a\sqrt 2 }}{2}}}{{a\sqrt 2 }} = \frac{1}{2} \Rightarrow \widehat {SAO} = 60^\circ \).

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Trong hình vẽ bên điểm M biểu diễn số phức \({z_1}\), điểm N biểu diễn số phức \({z_2}\). Hỏi trung điểm của đoạn MN là điểm biểu diễn hình học của số phức nào sau đây
   
   

   Câu hỏi:
   

   Trong hình vẽ bên điểm M biểu diễn số phức \({z_1}\), điểm N biểu diễn số phức \({z_2}\). Hỏi trung điểm của đoạn MN là điểm biểu diễn hình học của số phức nào sau đây
   

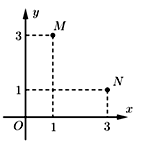
   A. \(z = 1 + i\)           

   B. \(z = 2 + 2i\)

   Đáp án chính xác

   C. \(z = 4 + 4i\)          

   D. \(z = 2 – 2i\)

   Trả lời:

   Đáp án B
   Điểm \(M\left( {1;3} \right),N\left( {3;1} \right)\) nên trung điểm của MN là \(I\left( {2;2} \right)\).
   Vậy \(z = 2 + 2i\).

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====