Cho hình lăng trụ đứng ABC.A'B'C' có BAC^=1200, BC=AA'=a. Gọi M là trung điểm của CC'. Tính khoảng cách giứa hai đường thẳng BM và AB', biết rằng chúng vuông góc với nhau.

Câu hỏi:

Cho hình lăng trụ đứng ABC.A’B’C’ có $\widehat{BAC}={120}^0$, $BC=A{A}^{‘}=a$. Gọi M là trung điểm của CC’. Tính khoảng cách giứa hai đường thẳng BM và AB’, biết rằng chúng vuông góc với nhau.

A. $\frac{a\sqrt{3}}{2}$

B. $\frac{a\sqrt{3}}{6}$

C. $\frac{a\sqrt{5}}{10}$

Đáp án chính xác

D. $\frac{a\sqrt{5}}{5}$

Trả lời:

Chọn C.

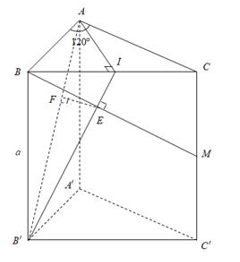
Gọi \(I\) là hình chiếu của A trên BC, ta có:
$\{\begin{array}{l}AI\perp BC\\ AI\perp BB‘\end{array}\Rightarrow AI\perp (BCC‘B‘)\Rightarrow AI\perp BM\left(1\right).$
Mặt khác, theo giả thiết: $A‘B\perp BM\left(2\right).$
Từ (1) và (2) suy ra $BM\perp (AB‘I)\Rightarrow BM\perp B‘I.$
Gọi $E=B‘I\cap BM,$ ta có: $\widehat{IBE}=\widehat{BB‘I}$(vì cùng phụ với góc $\widehat{BIB‘}).$
Khi đó $\Delta B‘BI=\Delta BCM(g.c.g)\Rightarrow BI=CM=\frac{a}{2}\Rightarrow I$là trung điểm cạnh $BC\Rightarrow \Delta ABC$ cân tại A.
Gọi F là hình chiếu của E trên \(AB’,\) ta có EF là đoạn vuông góc chung của AB’và BM
Suy ra $d(BM,AB‘)=EF.$
Ta có: $AI=BI.\cot {60}^0=\frac{a}{2}.\frac{\sqrt{3}}{3}=\frac{a\sqrt{3}}{6};B‘I=\sqrt{BB{‘}^2+B{I}^2}=\sqrt{a^2+{\left(\frac{a}{2}\right)}^2}=\frac{a\sqrt{5}}{2}=BM.$
$IE=BI.\sin \widehat{EBI}=BI.\frac{CM}{BM}=\frac{a}{2}.\frac{\frac{a}{2}}{\frac{a\sqrt{5}}{2}}=\frac{a\sqrt{5}}{10}\Rightarrow B‘E=B‘I-IE=\frac{2a\sqrt{5}}{5}.$
$AB‘=\sqrt{A{I}^2+B‘I{‘}^2}=\sqrt{{\left(\frac{a\sqrt{3}}{6}\right)}^2+{\left(\frac{a\sqrt{5}}{2}\right)}^2}=\frac{2a\sqrt{3}}{3}.$
Mặt khác: $\Delta B‘IA$ đồng dạng $\Delta B‘FE$ nên \(\frac{{B’A}}{{B’E}} = \frac{{IA}}{{EF}} \Leftrightarrow EF = \frac{{IAB’E}}{{B’A}} = \frac{{\frac{{a\sqrt 3 }}{6}.\frac{{2a\sqrt 5 }}{5}}}{{\frac{{2a\sqrt 3 }}{3}}} = \frac{{a\sqrt 5 }}{{10}}.\)
Vậy $d(BM,AB‘)=\frac{a\sqrt{5}}{10}.$

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Đường cong sau là đồ thị của một trong các hàm số cho dưới đây. Đó là hàm số nào? Chọn D.Ta có nên do đó loại đáp án A và C.Đồ thị hàm số đi qua điểm nên thay vào đáp án B và D ta thấy
   
   

   Câu hỏi:
   

   Đường cong sau là đồ thị của một trong các hàm số cho dưới đây. Đó là hàm số nào? 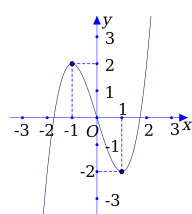Chọn D.Ta có nên do đó loại đáp án A và C.Đồ thị hàm số đi qua điểm 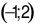nên thay 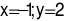vào đáp án B và D ta thấy

   A. .

   B. .

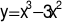   C.

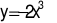
   D. .

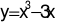   Đáp án chính xác

   Trả lời:

   Đáp án D: \(2 = {\left( { – 1} \right)^3} – 3\left( { – 1} \right)\) (luôn đúng).

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Tìm tất cả các giá trị của \(m\) để hàm số y=x3−3mx2+mx+2 có hai điểm cực trị.
   
   

   Câu hỏi:
   

   Tìm tất cả các giá trị của \(m\) để hàm số $y=x^3-3m{x}^2+mx+2$ có hai điểm cực trị.

   A. $[\begin{array}{c}m>\frac{1}{3}\\ m<0\end{array}$

   Đáp án chính xác

   B. $[\begin{array}{c}m>3\\ m<0\end{array}$

   C. $[\begin{array}{c}m\ge \frac{1}{3}\\ m\le 0\end{array}$

   D. $[\begin{array}{c}m\ge 3\\ m\le 0\end{array}$

   Trả lời:

   Chọn A.
   Ta có $y=x^3-3m{x}^2+mx+2\Rightarrow y‘=3x^2-6mx+m.$
   Hàm số có hai điểm cực trị \( \Leftrightarrow y’\) có hai nghiệm phân biệt $\iff \Delta ‘=9m^2-3m>0\iff [\begin{array}{l}m>\frac{1}{3}\\ m<0\end{array}.$

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Đường cong sau là đồ thị của hàm số nào trong các hàm số đã cho dưới đây?
   
   

   Câu hỏi:
   

   Đường cong sau là đồ thị của hàm số nào trong các hàm số đã cho dưới đây?
   

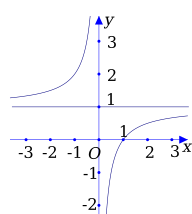
   A. $y=\frac{x}{1-x}$

   B. $y=\frac{x}{x-1}$

   C. $y=\frac{1-x}{x}$

   D. $y=\frac{x-1}{x}$

   Đáp án chính xác

   Trả lời:

   Chọn D.
   Từ đồ thị ta thấy, tiệm cận ngang là đường thẳng y=1 nên loại đáp án C và A.
   Đồ thị đi qua điểm A(1;0), nên chọn đáp án D.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Cho hình chóp SABCD có đáy ABCD là hình vuông cạnh 2a, SA=a, SA vuông góc với mặt đáy. Thể tích của khối chóp SABCD là
   
   

   Câu hỏi:
   

   Cho hình chóp SABCD có đáy ABCD là hình vuông cạnh 2a, SA=a, SA vuông góc với mặt đáy. Thể tích của khối chóp SABCD là

   A. $2a^3$

   B. $4a^3$

   C. $\frac{2}{3}{a}^3$

   D. $\frac{4}{3}{a}^3$

   Đáp án chính xác

   Trả lời:

   Chọn D.
   $S_{ABCD}=4a^2;V_{S.ABCD}=\frac{1}{3}{S}_{ABCD}.SA=\frac{1}{3}4a^2.a=\frac{4}{3}{a}^3.$

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Cho hàm số y=x4+bx2+c có đồ thị như hình vẽ sau: . Tính tổng b+c.
   
   

   Câu hỏi:
   

   Cho hàm số $y=x^4+b{x}^2+c$ có đồ thị như hình vẽ sau:
   .
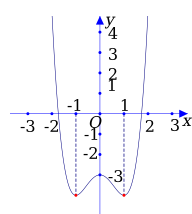   Tính tổng b+c.

   A. -3

   B. -5

   Đáp án chính xác

   C. -1

   D. -4

   Trả lời:

   Chọn B.
   Dựa vào đồ thị ta có:
   * $x=0;y=-3\Rightarrow c=-3$
   * Hàm số có đạt cực trị tại $x=0;x=\pm 1\Rightarrow y‘=4x^3+2bx=0$ có các nghiệm là $x=0;x=\pm 1\Rightarrow 4+2b=0\Rightarrow b=-2$
   Vậy b+c=5

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====