Câu hỏi:
Cho hình chóp SABCD có đáy ABCD là hình thang vuông tại A và Tính cosin của góc giữa hai mặt phẳng \(\left( {SBC} \right)\) và (SCD).
A.
B.
C.
D.
Đáp án chính xác
Trả lời:
Hướng dẫn gải:
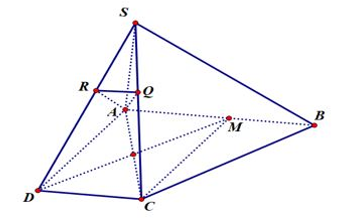
Gọi M là trung điểm AB, ta thấy ngay AMCD là hình vuông. MBCD là hình bình hành. Suy ra mà để chứng minh Trong tam giác vuông SAD vuông tại A vẽ đường cao AR như hình ta có và Trong tam giác vuông SAC vuông tại \(A\) vẽ đường cao AQ như hình ta có và Vậy góc giữa hai mặt phẳng \(\left( {SBC} \right)\) và (SCD) là góc giữa AR và AQ chính là góc \(\widehat {RAQ} = \alpha .\) Tam giác APQ vuông tại R có
Đáp án D
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho hình chóp tứ giác đều SABCD có cạnh đáy bằng 2a, chiều cao cạnh bên bằng 3a.Tính thể tích V của khối chóp đã cho.
Câu hỏi:
Cho hình chóp tứ giác đều SABCD có cạnh đáy bằng 2a, chiều cao cạnh bên bằng 3a.Tính thể tích V của khối chóp đã cho.
A.
B.
Đáp án chính xác
C.
D.\(V = \frac{{4{a^3}}}{3}.\)
Trả lời:
Chọn B.
* Diện tích đáy là:
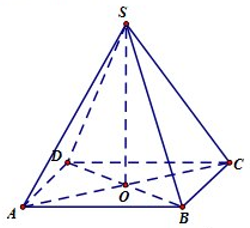
* Gọi là tâm của \(ABCD\) ta có thể tích V của khối chóp đã cho là:
là tâm của \(ABCD\) ta có thể tích V của khối chóp đã cho là: ====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho hai số thực dương a và b. Biểu thức abbaab35 được viết dưới dạng lũy thừa với số mũ hữu tỉ là:
Câu hỏi:
Cho hai số thực dương a và b. Biểu thức được viết dưới dạng lũy thừa với số mũ hữu tỉ là:
A.\({x^{\frac{7}{{30}}}}.\)
B.
C.
D.
Đáp án chính xác
Trả lời:
Chọn D.
Ta có:====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Gọi M,m thứ tự là giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y = \frac{{{x^2} + 3}}{{x – 1}}\) trên đoạn [-2;0] Tính P=M+m.
Câu hỏi:
Gọi M,m thứ tự là giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y = \frac{{{x^2} + 3}}{{x – 1}}\) trên đoạn [-2;0] Tính P=M+m.
A.P=1
B.
C.\(P = – \frac{{13}}{3}.\)
D.
Đáp án chính xác
Trả lời:
Chọn D.
Ta có suy ra
Xét trên [-2;0] ta có và \(f\left( 0 \right) = – 3.\)
Vậy và , do đó====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Tổng tất cả các giá trị nguyên của m để hàm số \(y = \frac{1}{3}{x^3} – \left( {m – 1} \right){x^2} + x – m\) đồng biến trên tập xác định bằng.
Câu hỏi:
Tổng tất cả các giá trị nguyên của m để hàm số \(y = \frac{1}{3}{x^3} – \left( {m – 1} \right){x^2} + x – m\) đồng biến trên tập xác định bằng.
A.3.
Đáp án chính xác
B.2.
C.4.
D. 1.
Trả lời:
Chọn A.
Tập xác định
Ta có để hàm số đồng biến với \(\forall x \in D\) thì mà nên Vậy đáp án là A.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Tính thể tích của khối chóp có chiều cao h và diện tích đáy là \(B\) là
Câu hỏi:
Tính thể tích của khối chóp có chiều cao h và diện tích đáy là \(B\) là
A.
Đáp án chính xác
B.
C.
D.
Trả lời:
Chọn A.
Áp dụng công thức tính thể tích khối chóp ta chọn đáp án A.====== **** mời các bạn xem câu tiếp bên dưới **** =====