Câu hỏi:
Cho hình chóp S.ABCD có SA vuông góc với đáy và \(SA = a\sqrt 3 ,\) đáy ABCD là hình vuông cạnh 2a. Gọi E là trung điểm của cạnh AD. Khoảng cách giữa SC và BE là
A. \(\frac{{2a\sqrt {17} }}{{17}}.\)
B. \(\frac{{4a\sqrt {17} }}{{17}}.\)
Đáp án chính xác
C. \(\frac{{4a\sqrt {53} }}{{53}}.\)
D. \(\frac{{2a\sqrt {53} }}{{53}}.\)
Trả lời:
Đáp án B
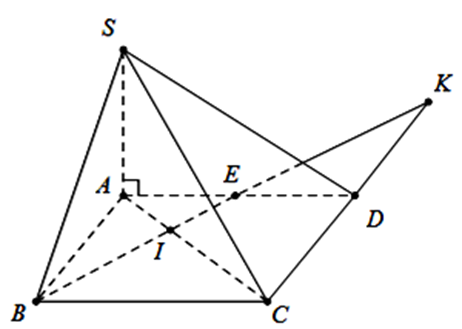
Ta có: \(h = SA = \sqrt 3 \)
Gọi \(I = AC \cap BE,K = BE \cap C{\rm{D}}\)
Áp dụng công thức \(\frac{1}{{{d^2}}} = \frac{1}{{{c^2}}} + \frac{{{k^2}}}{{{h^2}}}\)
Khi đó \(c = d\left( {C;BE} \right) \Rightarrow \frac{1}{{{c^2}}} = \frac{1}{{C{B^2}}} + \frac{1}{{C{K^2}}}\)
\(k = \frac{{CA}}{{CI}} = \frac{3}{2}\) (vì \(\frac{{IA}}{{IC}} = \frac{{A{\rm{E}}}}{{BC}} = \frac{1}{2}\))
Do đó \(\frac{1}{{{d^2}}} = \frac{1}{{C{B^2}}} + \frac{1}{{C{K^2}}} + \frac{{1,{5^2}}}{{{h^2}}} \Rightarrow d = \frac{{4{\rm{a}}\sqrt {17} }}{{17}}\).
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Trong không gian với hệ tọa độ \(Oxyz\), cho mặt phẳng \(\left( P \right):\frac{x}{3} + \frac{y}{2} + \frac{z}{1} = 1\). Vectơ nào dưới đây là vectơ pháp tuyến của \(\left( P \right)?\)
Câu hỏi:
Trong không gian với hệ tọa độ \(Oxyz\), cho mặt phẳng \(\left( P \right):\frac{x}{3} + \frac{y}{2} + \frac{z}{1} = 1\). Vectơ nào dưới đây là vectơ pháp tuyến của \(\left( P \right)?\)
A. \(\vec n = \left( {6;3;2} \right).\)
B. \(\vec n = \left( {2;3;6} \right).\)
Đáp án chính xác
C. \(\vec n = \left( {1;\frac{1}{2};\frac{1}{3}} \right).\)
D. \(\vec n = \left( {3;2;1} \right).\)
Trả lời:
Đáp án B
Mặt phẳng \(\left( P \right)\) có một VTPT là \(\overrightarrow {{n_1}} = \left( {\frac{1}{3};\frac{1}{2};\frac{1}{1}} \right) = \frac{1}{6}\left( {2;3;6} \right) = \frac{1}{6}\overrightarrow n \Rightarrow \overrightarrow n \) cũng là một VTPT của \(\left( P \right)\).====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho \(a > 0,{\mkern 1mu} {\mkern 1mu} a \ne 1\) và \(x,y\) là hai số thực dương tùy ý. Khẳng định nào sau đây là khẳng định đúng?
Câu hỏi:
Cho \(a > 0,{\mkern 1mu} {\mkern 1mu} a \ne 1\) và \(x,y\) là hai số thực dương tùy ý. Khẳng định nào sau đây là khẳng định đúng?
A. \({\log _a}\left( {x – y} \right) = \frac{{{{\log }_a}x}}{{{{\log }_b}y}}.\)
B. \({\log _a}\frac{x}{y} = \frac{{{{\log }_a}x}}{{{{\log }_b}y}}.\)
C. \({\log _a}\frac{x}{y} = {\log _a}x – {\log _b}y.\)
Đáp án chính xác
D. \({\log _a}\left( {x – y} \right) = {\log _a}x – {\log _b}y.\)
Trả lời:
Đáp án C
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho hàm số \(y = f\left( x \right)\). Biết rằng hàm số f(x) có đạo hàm là \(f'\left( x \right)\) và hàm số \(y = f'\left( x \right)\) có đồ thị như hình vẽ bên. Khẳng định nào sau đây sai?
Câu hỏi:
Cho hàm số \(y = f\left( x \right)\). Biết rằng hàm số f(x) có đạo hàm là \(f’\left( x \right)\) và hàm số \(y = f’\left( x \right)\) có đồ thị như hình vẽ bên. Khẳng định nào sau đây sai?
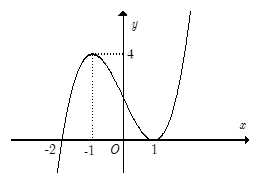
A. Hàmf(x) nghịch biến trên khoảng \(\left( { – \infty ; – 2} \right).\)
B. Hàm f(x) đồng biến trên khoảng \(\left( {1; + \infty } \right)\).
C. Trên \(\left( { – 1;1} \right)\) thì hàm số f(x) luôn tăng.
D. Hàm f(x) giảm trên đoạn có độ dài bằng 2.
Đáp án chính xác
Trả lời:
Đáp án D
Dựa vào đồ thị hàm số \(y = f’\left( x \right)\) ta có bảng xét dấu \(f’\left( x \right)\).

Dựa vào bảng xét dấu ta thấy:
Hàm \(f\left( x \right)\) nghịch biến trên khoảng \(\left( { – \infty ; – 2} \right)\) suy ra A đúng.
Hàm \(f\left( x \right)\) đồng biến trên khoảng \(\left( {1; + \infty } \right)\) suy ra B đúng.
Trên \(\left( { – 1;1} \right)\) thì hàm số \(f\left( x \right)\) luôn tăng suy ra C đúng suy ra chọn D.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Phương trình \({4^{2x + 1}} = 32\) có nghiệm là
Câu hỏi:
Phương trình \({4^{2x + 1}} = 32\) có nghiệm là
A. \(x = \frac{5}{2}.\)
B. \(x = \frac{5}{4}.\)
C. \(x = \frac{3}{4}.\)
Đáp án chính xác
D. \(x = 1.\)
Trả lời:
Đáp án C
Ta có: \({4^{2{\rm{x}} + 1}} = 32 \Leftrightarrow {2^{2\left( {2{\rm{x}} + 1} \right)}} = {2^5} \Leftrightarrow 4{\rm{x}} + 2 = 5 \Leftrightarrow x = \frac{3}{4}\).====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho cấp số cộng \({u_n}\) có các số hạng đầu lần lượt là 5; 9; 13; 17;…Tìm số hạng tổng quát \({u_n}\) của cấp số cộng?
Câu hỏi:
Cho cấp số cộng \({u_n}\) có các số hạng đầu lần lượt là 5; 9; 13; 17;…Tìm số hạng tổng quát \({u_n}\) của cấp số cộng?
A. \({u_n} = 4n + 1.\)
Đáp án chính xác
B. \({u_n} = 5n – 1.\)
C. \({u_n} = 5n + 1.\)
D. \({u_n} = 4n – 1.\)
Trả lời:
Đáp án A
Dãy số đã cho là cấp số cộng có \({u_1} = 5;{u_2} = 9 \Rightarrow d = {u_2} – {u_1} = 9 – 5 = 4\).
Do đó \({u_n} = {u_1} + \left( {n – 1} \right)d = 5 + 4\left( {n – 1} \right) = 4n + 1\).
Vậy \({u_n} = 4n + 1\).====== **** mời các bạn xem câu tiếp bên dưới **** =====