Câu hỏi:
Cho hình chóp S.ABCD có SA vuông góc với đáy, \(SA = a\sqrt 6 .\) Đáy ABCD là hình thang vuông tại A và \(B,{\mkern 1mu} {\mkern 1mu} AB = BC = \frac{1}{2}AD = a.\) Gọi E là trung điểm AD. Tính bán kính mặt cầu ngoại tiếp hình chóp \(S.ECD\).
A. \(a\sqrt 6 .\)
B. \(a\sqrt {\frac{{19}}{6}} .\)
Đáp án chính xác
C. \(\frac{{a\sqrt {30} }}{3}.\)
D. \(a\sqrt {\frac{{114}}{6}} .\)
Trả lời:
Đáp án B
Ta có: \({\rm{CE // AB}} \Rightarrow {\rm{CE}} \bot A{\rm{D}}\)
Mặt khác \(CE \bot {\rm{S}}A \Rightarrow CE \bot \left( {SE{\rm{D}}} \right)\)
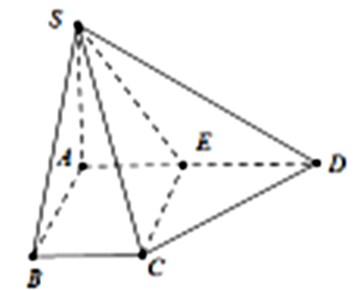
\( \Rightarrow {R_{C.SE{\rm{D}}}} = \sqrt {\frac{{C{E^2}}}{4} + {{\left( {{R_{S{\rm{D}}E}}} \right)}^2}} \)
Lại có \(CE = AB = a,{\rm{ }}\sin \widehat {SE{\rm{A}}} = \sin \widehat {SE{\rm{D}}}\)
\( = \frac{{SA}}{{SE}} = \frac{{a\sqrt 6 }}{{\sqrt {{a^2} + 6{{\rm{a}}^2}} }} = \frac{{a\sqrt 6 }}{{\sqrt 7 }}\)
\( \Rightarrow {R_{SE{\rm{D}}}} = \frac{{S{\rm{D}}}}{{2\sin \widehat {SE{\rm{D}}}}} = \frac{{a\sqrt {10} }}{{2.\frac{{a\sqrt 6 }}{{\sqrt 7 }}}} = \frac{{a\sqrt {105} }}{6}\)
Vậy \({R_{S.C{\rm{D}}E}} = a\sqrt {\frac{{19}}{6}} \).
Cách 2: Do \(\left( {SE{\rm{D}}} \right) \bot \left( {CE{\rm{D}}} \right) \Rightarrow R = \sqrt {R_1^2 + R_2^2 – \frac{{G{T^2}}}{4}} \) trong đó \({R_1} = {R_{SE{\rm{D}}}} = \frac{{a\sqrt {105} }}{6}\),
\({R_2} = {R_{CE{\rm{D}}}} = \frac{{C{\rm{D}}}}{2} = \frac{{a\sqrt 2 }}{2}\) và \(GT = E{\rm{D}} = a \Rightarrow R = a\sqrt {\frac{{19}}{6}} \).
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Từ một nhóm có 10 học sinh nam và 15 học sinh nữ. Hỏi có bao nhiêu cách chọn ra 2 học sinh nam và 3 học sinh nữ để lập thành một đội 5 bạn đi biễu diễn văn nghệ
Câu hỏi:
Từ một nhóm có 10 học sinh nam và 15 học sinh nữ. Hỏi có bao nhiêu cách chọn ra 2 học sinh nam và 3 học sinh nữ để lập thành một đội 5 bạn đi biễu diễn văn nghệ
A. \(C_{25}^5.\)
B. \(C_{10}^2C_{15}^3.\)
Đáp án chính xác
C. \(C_{10}^2 + C_{15}^3.\)
D. \(A_{10}^2.A_{15}^3.\)
Trả lời:
Đáp án B
Chọn ra 2 học sinh nam có \(C_{10}^2\) cách, chọn ra 3 học sinh nữ có \(C_{15}^3\) cách.
Theo quy tắc nhân có \(C_{10}^2.C_{15}^3\) cách để chọn ra 2học sinh nam và 3 học sinh nữ để lập thành một đội 5 bạn đi biểu diễn văn nghệ.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Trong không gian Oxyz cho mặt phẳng \((P):2x – y + z – 1 = 0\) đi qua điểm nào sau đây?
Câu hỏi:
Trong không gian Oxyz cho mặt phẳng \((P):2x – y + z – 1 = 0\) đi qua điểm nào sau đây?
A. \(P(1; – 2;0).\)
B. \(M(2; – 1;1).\)
C. \(Q(1; – 3; – 4).\)
Đáp án chính xác
D. \(N(0;1; – 2).\)
Trả lời:
Đáp án C
Thay lần lượt tọa độ điểm M, N, P, Q vào mặt phẳng \(\left( P \right):2{\rm{x}} – y + z – 1 = 0\) ta được:
\(P\left( {1; – 2;0} \right) \to 2.1 – \left( { – 2} \right) + 0 – 1 = – 1 \ne 0 \to P \notin \left( P \right)\)
\(M\left( {2; – 1;1} \right) \to 2.2 – \left( { – 1} \right) + 1 – 1 = 5 \ne 0 \to M \notin \left( P \right)\)
\(Q\left( {1; – 3; – 4} \right) \to 2.1 – \left( { – 3} \right) – 4 – 1 = 0 \to Q \in \left( P \right)\)
\(N\left( {0;1; – 2} \right) \to 2.0 – 1 – 2 – 1 = – 4 \ne 0 \to N \notin \left( P \right)\).====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Lăng trụ có chiều cao bằng a đáy là tam giác vuông cân và có thể tích bằng \(2{a^3}\) .Cạnh góc vuông của đáy lăng trụ bằng
Câu hỏi:
Lăng trụ có chiều cao bằng a đáy là tam giác vuông cân và có thể tích bằng \(2{a^3}\) .Cạnh góc vuông của đáy lăng trụ bằng
A. \(3a.\)
B. \(2a.\)
Đáp án chính xác
C. \(a.\)
D. \(4a.\)
Trả lời:
Đáp án B
Giả sử đáy của lăng trụ đã cho là tam giác ABC vuông cân tại A.
Khi đó \({S_{ABC}} = \frac{{2{{\rm{a}}^3}}}{a} = 2{{\rm{a}}^2} \Leftrightarrow \frac{1}{2}A{B^2} = 2{{\rm{a}}^2} \Leftrightarrow AB = 2{\rm{a}}\).====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho số phức \(z = 1 + 2i\) . Tìm tổng phần thực và phần ảo của số phức \(w = 2z + \bar z\) .
Câu hỏi:
Cho số phức \(z = 1 + 2i\) . Tìm tổng phần thực và phần ảo của số phức \(w = 2z + \bar z\) .
A. 3.
B. 5.
Đáp án chính xác
C. 1.
D. 2.
Trả lời:
Đáp án B
\({\rm{w}} = 2{\rm{z}} + \overline z = 2\left( {1 + 2i} \right) + \left( {1 – 2i} \right) = 3 + 2i\).
Suy ra, phần thực của số phức \({\rm{w}} = 2{\rm{z}} + \overline z \) là 3; phần ảo của số phức \({\rm{w}} = 2{\rm{z}} + \overline z \) là 2.
Do đó, tổng phần thực và phần ảo của số phức \({\rm{w}} = 2{\rm{z}} + \overline z \) là 5.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Trong không gian Oxyz, đường thẳng \(d:\frac{{x – 3}}{1} = \frac{{y + 2}}{{ – 1}} = \frac{{z – 4}}{2}\) cắt mặt phẳng \(\left( {Oxy} \right)\)tại điểm có tọa độ là
Câu hỏi:
Trong không gian Oxyz, đường thẳng \(d:\frac{{x – 3}}{1} = \frac{{y + 2}}{{ – 1}} = \frac{{z – 4}}{2}\) cắt mặt phẳng \(\left( {Oxy} \right)\)tại điểm có tọa độ là
A. \(\left( { – 1;0;0} \right).\)
B. \(\left( { – 3;2;0} \right).\)
C. \(\left( {1;0;0} \right).\)
Đáp án chính xác
D. \(\left( {3; – 2;0} \right).\)
Trả lời:
Đáp án C
Ta có \(d:\left\{ \begin{array}{l}x = 3 + t\\y = – 2 – t\\z = 4 + 2t\end{array} \right.\) nên đồ thị hàm số cắt \(\left( {Oxy} \right)\) tại \(\left( {1;0;0} \right)\).====== **** mời các bạn xem câu tiếp bên dưới **** =====