Câu hỏi:
Cho hàm số xác định là liên tục trên R và có đồ thị như hình vẽ
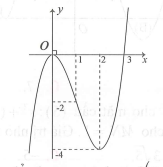
Số giá trị nguyên của tham số m để phương trình có đúng hai nghiệm phân biệt thuộc đoạn là
A. 4.
B. 8.
C. 6.
Đáp án chính xác
D. 5.
Trả lời:
Đáp án C
Đặt .
Ta có: .
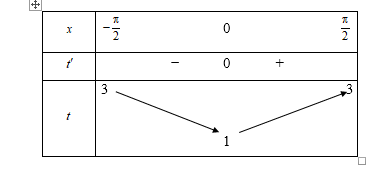
Nhận xét:
+ Với , suy ra phương trình (1) không có nghiệm thuộc .
+ Với t=1 , suy ra phương trình (1) có một nghiệm thuộc .
+ Với , suy ra phương trình (1) có hai nghiệm thuộc .
Lúc đó, phương trình đã cho trở thành .
Để phương trình đã cho có đúng 2 nghiệm thì .
Vì nên .
Vậy có 6 giá trị nguyên thỏa mãn điều kiện bài toán.
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Câu 1. Thể tích của khối lập phương cạnh 2a bằng
Câu hỏi:
Câu 1. Thể tích của khối lập phương cạnh bằng
A.
Đáp án chính xác
B.
C.
D.
Trả lời:
Đáp án A
Thể tích khối lập phương cạnh là:====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho hàm số y=x4−2×2+3 , giá trị cực tiểu của hàm số đã cho bằng
Câu hỏi:
Cho hàm số , giá trị cực tiểu của hàm số đã cho bằng
A. 2.
Đáp án chính xác
B. 3
C. -1
D. 1.
Trả lời:
Đáp án A
TXĐ: .
Ta có:
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Trong không gian với hệ trục tọa độ Oxyz, tọa độ của véctơ u→=2i→−3j→+4k→ là
Câu hỏi:
Trong không gian với hệ trục tọa độ Oxyz, tọa độ của véctơ là
A. .
Đáp án chính xác
B.
C. .
D. .
Trả lời:
Đáp án A
Ta có: .
Lưu ý: Ta có thể chỉ cần đọc các hệ số lần lượt của các véctơ tương ứng.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho hàm số y=fx có bảng biến thiên như hình dưới đây. Mệnh đề nào sau đây là đúng?
Câu hỏi:
Cho hàm số có bảng biến thiên như hình dưới đây. Mệnh đề nào sau đây là đúng?
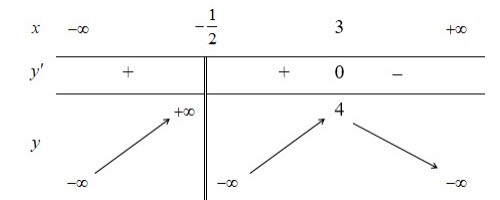
A. Hàm số đã cho nghịch biến trên các khoảng và .
B. Hàm số đã cho đồng biến trên khoảng .
C. Hàm số đã cho đồng biến trên khoảng .
D. Hàm số đã cho nghịch biến trên khoảng .
Đáp án chính xác
Trả lời:
Đáp án D
Ta thấy trên khoảng thì , suy ra hàm số nghịch biến trên khoảng .
Lưu ý: Tại , hàm số bị gián đoạn; vậy không thể nói hàm số đơn điệu trên khoảng====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Với a và b là hai số thực dương tùy ý, logab2 bằng
Câu hỏi:
Với và là hai số thực dương tùy ý, bằng
A. .
B. .
Đáp án chính xác
C. .
D. .
Trả lời:
Đáp án B
Ta có: .====== **** mời các bạn xem câu tiếp bên dưới **** =====