Cho hàm số y=fx  có bảng biến thiên như sau: Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là

Câu hỏi:

Cho hàm số $y=f\left(x\right)$  có bảng biến thiên như sau:

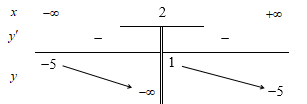
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là

A. 4.

A. 4.

C. 2.

Đáp án chính xác

C. 2.

Trả lời:

Đáp án C
Dựa vào bảng biến thiên ta có:
+ $\underset{x\to \pm \infty }{\lim }f\left(x\right)=-5$ , nên đường thẳng $y=-5$  là một tiệm cận ngang của đồ thị hàm số.
+ $\underset{x\to 2^{-}}{\lim }f\left(x\right)=-\infty$  nên đường thẳng $x=2$  là một tiệm cận đứng của đồ thị hàm số.
Vậy đồ thị hàm số đã cho có 2 tiệm cận.

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Câu 1. Thể tích của khối lập phương cạnh 2a  bằng
   
   

   Câu hỏi:
   

   Câu 1. Thể tích của khối lập phương cạnh $2a$  bằng

   A. $8a^3$

   Đáp án chính xác

   B. $2a^3$

   C. $a^3$ 

   D. $6a^3$

   Trả lời:

   Đáp án A
   Thể tích khối lập phương cạnh $2a$ là: $V={\left(2a\right)}^3=8a^3$

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Cho hàm số y=x4−2×2+3 , giá trị cực tiểu của hàm số đã cho bằng
   
   

   Câu hỏi:
   

   Cho hàm số $y=x^4-2x^2+3$ , giá trị cực tiểu của hàm số đã cho bằng

   A. 2.

   Đáp án chính xác

   B. 3

   C. -1

   D. 1.

   Trả lời:

   Đáp án A
   TXĐ: $D=ℝ$  .
   Ta có:$y^{‘}=4x^3-4x=0\iff \left[\begin{array}{l}x=0\\ x=\pm 1\end{array}\right.$
    
    

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Trong không gian với hệ trục tọa độ Oxyz, tọa độ của véctơ u→=2i→−3j→+4k→  là
   
   

   Câu hỏi:
   

   Trong không gian với hệ trục tọa độ Oxyz, tọa độ của véctơ $\overrightarrow{u}=2\overrightarrow{i}-3\overrightarrow{j}+4\overrightarrow{k}$  là

   A. $\left(2;-3;4\right)$ .

   Đáp án chính xác

   B. $\left(-3;2;4\right)$

   C.$\left(2;3;4\right)$ .

   D.$\left(2;4;-3\right)$ .

   Trả lời:

   Đáp án A
   Ta có: $\overrightarrow{u}=2\overrightarrow{i}-3\overrightarrow{j}+4\overrightarrow{k}\Rightarrow \overrightarrow{u}\left(2;-3;4\right)$  .
   Lưu ý: Ta có thể chỉ cần đọc các hệ số lần lượt của các véctơ $\overrightarrow{i};\overrightarrow{j};\overrightarrow{k}$  tương ứng.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Cho hàm số y=fx  có bảng biến thiên như hình dưới đây. Mệnh đề nào sau đây là đúng?
   
   

   Câu hỏi:
   

   Cho hàm số $y=f\left(x\right)$  có bảng biến thiên như hình dưới đây. Mệnh đề nào sau đây là đúng?
   

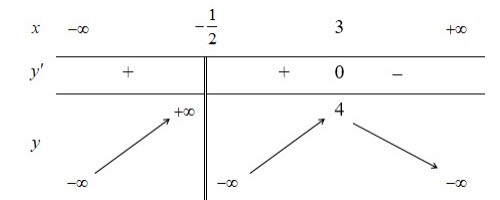
   A. Hàm số đã cho nghịch biến trên các khoảng $\left(-\infty ;-\frac{1}{2}\right)$  và $\left(3;+\infty \right)$ .

   B. Hàm số đã cho đồng biến trên khoảng$\left(-\frac{1}{2};+\infty \right)$ .

   C. Hàm số đã cho đồng biến trên khoảng $\left(-\infty ;3\right)$  .

   D. Hàm số đã cho nghịch biến trên khoảng $\left(3;+\infty \right)$ .    

   Đáp án chính xác

   Trả lời:

   Đáp án D
   Ta thấy trên khoảng $\left(3;+\infty \right)$  thì , suy ra hàm số nghịch biến trên khoảng $\left(3;+\infty \right)$  .
   Lưu ý: Tại $x=-\frac{1}{2}$ , hàm số bị gián đoạn; vậy không thể nói hàm số đơn điệu trên khoảng $\left(-\infty ;3\right)$

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Với a  và b  là hai số thực dương tùy ý, logab2  bằng
   
   

   Câu hỏi:
   

   Với $a$  và $b$  là hai số thực dương tùy ý, $\log \left(a{b}^2\right)$  bằng

   A. $2\log a+\log b$ .    

   B.$\log a+2\log b$ .

   Đáp án chính xác

   C.$2\left(\log a+\log b\right)$ .

   D. $\log a+\frac{1}{2}\log b$ .

   Trả lời:

   Đáp án B
   Ta có: $\log \left(a{b}^2\right)=\log a+\log b^2=\log a+2\log b$  .

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====