Câu hỏi:
Cho hàm số \(y = f(x)\) xác định trên \(\mathbb{R}\backslash \left\{ 0 \right\}\)và liên tục trên từng khoảng xác định. Biết hàm số có bảng biến thiên như hình vẽ dưới
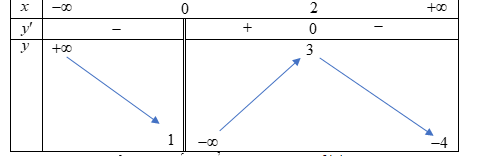
Tìm tâp hợp các giá trị của tham số \(m\)để phương trình \(f(x) = m\)có hai nghiệm thực phân biệt.
A. \(\left( { – 4;1} \right) \cup \left\{ 3 \right\}\).
B. \(\left( { – 4;1} \right] \cup \left\{ 3 \right\}\).
Đáp án chính xác
C. \(\left( { – \infty ;1} \right]\).
D. \(\left( { – 4;1} \right)\).
Trả lời:
Ta có số nghiệm của phương trình \(f(x) = m\)là số giao điểm của đồ thị hàm số \(y = f(x)\)và đường thẳng \(y = m\).
Dựa vào bảng biến thiên, để phương trình có hai nghiệm thực phân biệt ta được
\(m \in \left( { – 4;1} \right] \cup \left\{ 3 \right\}\)
Chọn đáp án B
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Hỏi có bao nhiêu cách xếp bốn bạn An, Bình, Cường, Dũng ngồi vào một bàn học gồm bốn chỗ?
Câu hỏi:
Hỏi có bao nhiêu cách xếp bốn bạn An, Bình, Cường, Dũng ngồi vào một bàn học gồm bốn chỗ?
A. \(6\).
B. \(4\).
C. \(1\).
D. \(24\).
Đáp án chính xác
Trả lời:
Xếp bốn bạn vào bốn vị trí ngồi \( \Rightarrow \) có \(4! = 24\) cách xếp
Chọn đáp án D====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho cấp số cộng \(\left( {{u_n}} \right)\) có \({u_1} = 2\) và \({u_5} = 10\). Tính tổng \(5\) số hạng đầu của cấp số cộng \(\left( {{u_n}} \right)\).
Câu hỏi:
Cho cấp số cộng \(\left( {{u_n}} \right)\) có \({u_1} = 2\) và \({u_5} = 10\). Tính tổng \(5\) số hạng đầu của cấp số cộng \(\left( {{u_n}} \right)\).
A. \({S_5} = 30\).
Đáp án chính xác
B. \({S_5} = 12\).
C. \({S_5} = 60\).
D. \({S_5} = 24\).
Trả lời:
Tổng \(5\) số hạng đầu của cấp số cộng \(\left( {{u_n}} \right)\) là \({S_5} = \frac{{5.\left( {{u_1} + {u_5}} \right)}}{2} = \frac{{5.\left( {2 + 10} \right)}}{2} = 30\).
Chọn đáp án A====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Tập nghiệm của bát phương trình \({3^{2x – 3}} >27\) là
Câu hỏi:
Tập nghiệm của bát phương trình \({3^{2x – 3}} >27\) là
A. \(\left( { – \infty \,;\,15} \right)\).
B. \(\left( {15\,;\, + \infty } \right)\).
C. \(\left( { – \infty \,;\,3} \right)\).
D. \(\left( {3\,;\, + \infty } \right)\).
Đáp án chính xác
Trả lời:
Ta có \({3^{2x – 3}} >27 \Leftrightarrow 2x – 3 >3 \Leftrightarrow 2x >6 \Leftrightarrow x >3\).
Vậy tập nghiệm của bất phương trình đã cho là \(\left( {3\,;\, + \infty } \right)\).
Chọn đáp án D====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Thể tích khối lăng trụ có chiều cao bẳng \(2\) và diện tích đáy bằng \(6\) là
Câu hỏi:
Thể tích khối lăng trụ có chiều cao bẳng \(2\) và diện tích đáy bằng \(6\) là
A. \(12\).
Đáp án chính xác
B. \(4\).
C. \(8\).
D. \(6\).
Trả lời:
Thể tích khối lăng trụ có chiều cao bẳng \(2\) và diện tích đáy bằng \(6\) là \(V = 2\,.\,6 = 12\).
Chọn đáp án A====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Tập xác định của hàm số \(y = {\log _5}\left( {2x + 1} \right)\) là
Câu hỏi:
Tập xác định của hàm số \(y = {\log _5}\left( {2x + 1} \right)\) là
A. \(\left[ { – \frac{1}{2}; + \infty } \right)\).
B. \(\left( { – \frac{1}{2}; + \infty } \right)\).
C. \(\left( { – \infty ; – \frac{1}{2}} \right)\).
Đáp án chính xác
D. \(\left( { – \infty ; – \frac{1}{2}} \right]\).
Trả lời:
Điều kiện xác định là \(2x + 1 >0 \Leftrightarrow x >- \frac{1}{2}\).
Do đó, tập xác định của hàm số là \(\left( { – \frac{1}{2}; + \infty } \right)\).
Chọn đáp án C====== **** mời các bạn xem câu tiếp bên dưới **** =====