Câu hỏi:
Cho hàm số \(y = f(x) = a{x^3} + b{x^2} + cx + d\) có đồ thị như hình vẽ:
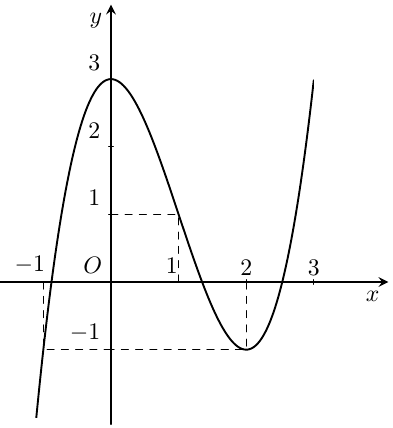
Có bao nhiêu giá trị nguyên của \(m\)thuộc đoạn \(\left[ { – 10;10} \right]\) để phương trình \(f\left( {{{\rm{e}}^x} – x + m} \right) = 1\) có \(6\) nghiệm phân biệt?
A. \(11\).
B. \(12\).
C. \(10\).
D. \(9\).
Đáp án chính xác
Trả lời:
Chọn đáp án D
Từ đồ thị, ta thấy
\(f\left( {{{\rm{e}}^x} – x + m} \right) = 1\; \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{{{\rm{e}}^x} – x + m = a}\\{{{\rm{e}}^x} – x + m = 1}\\{{{\rm{e}}^x} – x + m = b}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{{{\rm{e}}^x} – x – a = – m}\\{{{\rm{e}}^x} – x – 1 = – m}\\{{{\rm{e}}^x} – x – b = – m}\end{array}} \right.\)
trong đó \(a \in \left( { – 1;0} \right),\) \(b \in \left( {2;3} \right).\)
Xét hàm số \(f\left( x \right) = {{\rm{e}}^x} – x – \alpha \), với \(\alpha \in \left\{ {a;1;b} \right\}\) và \(x \in \mathbb{R}\).
Ta có \(f’\left( x \right) = {{\rm{e}}^x} – 1\) và \(f’\left( x \right) = 0\; \Leftrightarrow x = 0\).
Bảng biến thiên của \(f\left( x \right):\)
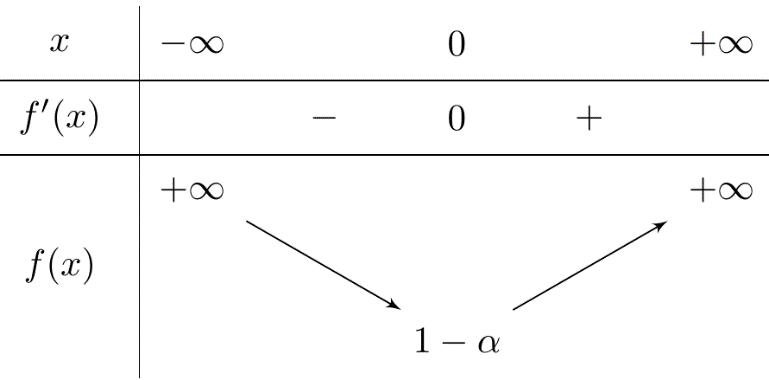
Vì \(a < 0 < 1 < 2 < b\) nên \(1 – a >1 >1 – b\). Do đó, kết hợp với bảng biến thiên ở trên ta thấy rằng, phương trình đã cho có 6 nghiệm phân biệt khi và chỉ khi</>
\( – m >1 – a\; \Leftrightarrow m < a – 1.\)
Vì \( – 1 < a < 0\,\, \Leftrightarrow \,\, – 2 < a – 1 < – 1\) nên các giá trị nguyên của \(m\) trên đoạn \(\left[ { – 10;10} \right]\) là
\( – 10;\; – 9;\; – 8;\; – 7;\; – 6; – 5; – 4; – 3; – 2.\)
Vậy có 9 giá trị nguyên của m thỏa mãn bài toán.
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Lớp 12A có 18 học sinh nữ và 17 học sinh nam. Giáo viên Chọn đáp án 1 học sinh trong lớp làm tình nguyện viên tham gia phong trào thanh niên của nhà trường. Hỏi có bao nhiêu cách chọn
Câu hỏi:
Lớp 12A có 18 học sinh nữ và 17 học sinh nam. Giáo viên Chọn đáp án 1 học sinh trong lớp làm tình nguyện viên tham gia phong trào thanh niên của nhà trường. Hỏi có bao nhiêu cách chọn
A.306.
B. 1.
C. 35.
Đáp án chính xác
D. 17.
Trả lời:
Chọn đáp án C
Tổng số học sinh của lớp là \(18 + 17 = 35\).
Số cách chọn 1 học sinh trong lớp là 35 cách.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho cấp số nhân
\(\left( {{u_n}} \right)\) với \({u_1} = \,3\) và \({u_2} = 12\). Công bội của cấp số nhân đã cho bằng
Câu hỏi:
Cho cấp số nhân
\(\left( {{u_n}} \right)\) với \({u_1} = \,3\) và \({u_2} = 12\). Công bội của cấp số nhân đã cho bằngA.4.
Đáp án chính xác
B. 3.
C. 9.
D.\(\frac{1}{4}\).
Trả lời:
Chọn đáp án A
Ta có: \({u_2} = {u_1}.q \Rightarrow q = \frac{{{u_2}}}{{{u_1}}} = \frac{{12}}{3}\, = \,4\).====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Phương trình \({4^x} – {3.2^x} + 2 = 0\) có nghiệm thuộc khoảng
Câu hỏi:
Phương trình \({4^x} – {3.2^x} + 2 = 0\) có nghiệm thuộc khoảng
A. \(\left( {\frac{1}{2};2} \right)\).
Đáp án chính xác
B. \(\left( {2;4} \right)\).
C.\(\left( { – 1;0} \right)\).
D. \(\left( {3;6} \right)\).
Trả lời:
Chọn đáp án A
\({4^x} – {3.2^x} + 2 = 0 \Leftrightarrow \left[ \begin{array}{l}{2^x} = 1\\{2^x} = 2\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 1 \in \left( {\frac{1}{2};2} \right)\end{array} \right.\).====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Thể tích khối chóp có đường cao bằng \(a\) và diện tích đáy bằng \(2{a^2}\sqrt 3 \) là
Câu hỏi:
Thể tích khối chóp có đường cao bằng \(a\) và diện tích đáy bằng \(2{a^2}\sqrt 3 \) là
A.\(\frac{{2{a^3}\sqrt 3 }}{3}\).
Đáp án chính xác
B.\(\frac{{2{a^3}\sqrt 3 }}{2}\).
C.\(\frac{{2{a^3}}}{3}\).
D.\(\frac{{5{a^3}}}{{\sqrt 3 }}\).
Trả lời:
Chọn đáp án A
Thể tích khối chóp là \(V = \frac{1}{3}.a.2{a^2}\sqrt 3 = \frac{{2{a^3}\sqrt 3 }}{3}\).====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Tập xác định của hàm số \(y = {\log _3}\left( {x – 1} \right)\) là
Câu hỏi:
Tập xác định của hàm số \(y = {\log _3}\left( {x – 1} \right)\) là
A. \(\left( {1; + \infty } \right)\).
Đáp án chính xác
B. \(\left[ {1; + \infty } \right)\).
C. \(\left( { – \infty ;1} \right)\).
D.\(\left( {3; + \infty } \right)\).
Trả lời:
Chọn đáp án A
Hàm số \(y = {\log _3}\left( {x – 1} \right)\) có nghĩa khi \(x – 1 >0 \Rightarrow x >1\).
Vậy tập xác định của hàm số \(y = {\log _3}\left( {x – 1} \right)\) là \(\left( {1; + \infty } \right)\).====== **** mời các bạn xem câu tiếp bên dưới **** =====