Cho hàm số \(f(x)\)có bảng biến thiên như sau: Hàm số đồng biến trên khoảng nào?

Câu hỏi:

Cho hàm số \(f(x)\)có bảng biến thiên như sau:

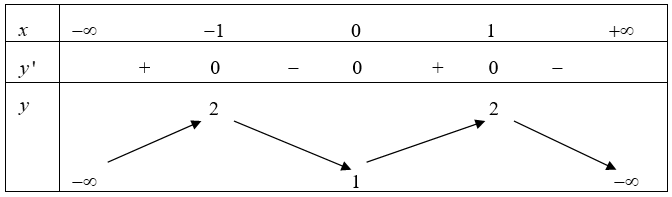
Hàm số đồng biến trên khoảng nào?

A.\((0;1)\)

Đáp án chính xác

B.$(-1;0)$

C.\(( – 1;1)\)

D.\((1; + \infty )\)

Trả lời:

Nhìn vào BBT ta dễ thấy hàm số đồng biến trên khoảng (0,1)
Đáp án A

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Giá trị lớn nhất của hàm số \(f(x) = {x^4} – 4{x^2} + 5\)trên đoạn \([ – 2;3]\)bằng:
   
   

   Câu hỏi:
   

   Giá trị lớn nhất của hàm số \(f(x) = {x^4} – 4{x^2} + 5\)trên đoạn \([ – 2;3]\)bằng:

   A.5

   B.50

   Đáp án chính xác

   C.1

   D.122

   Trả lời:

   Ta có \(f’\left( x \right) = 4{x^3} – 8x = 4x\left( {{x^2} – 2} \right).\)
   Giải $f‘\left(x\right)=0\iff [\begin{array}{l}x=0\in [-2;3]\\ x=\sqrt{2}\in [-2;3]\\ x=-\sqrt{2}\in [-2;3]\end{array}$
   Tính $f\left(0\right)=5;f\left(\sqrt{2}\right)=1;f(-\sqrt{2})=1;f(-2)=5;f\left(3\right)=50.$

   Suy ra \(\mathop {\max }\limits_{\left[ { – 2;3} \right]} y = 50 = f\left( 3 \right).\)
   Đáp án B

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Cho hàm số \(y = a{x^4} + b{x^2} + c(a,b,c \in R)\)có đồ thị như hình vẽ bên. Số điểm cực trị của hàm số đã cho là?
   
   

   Câu hỏi:
   

   Cho hàm số \(y = a{x^4} + b{x^2} + c(a,b,c \in R)\)có đồ thị như hình vẽ bên.
   
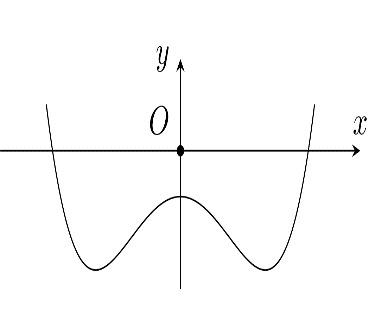
   Số điểm cực trị của hàm số đã cho là?

   A.3

   Đáp án chính xác

   B.2.

   C.1

   D.0

   Trả lời:

   Từ đồ thị ta có hàm số có ba điểm cực trị.
   Đáp án A

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Hàm số \(y = {2^{{x^2} – x}}\) có đạo hàm là
   
   

   Câu hỏi:
   

   Hàm số \(y = {2^{{x^2} – x}}\) có đạo hàm là

   A.\({2^{{x^2} – x}}.\ln 2\).

   B.\((2x – 1){.2^{{x^2} – x}}.\ln 2\).

   Đáp án chính xác

   C.\(({x^2} – x){.2^{{x^2} – x – 1}}\).

   D.\((2x – 1){.2^{{x^2} – x}}\).

   Trả lời:

   Do \(\left( {{a^u}} \right)’ = u’.{a^u}\ln a\) nên chọn B.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Tìm tập xác định \(D\) của hàm số \(y = {\log _3}\left( {{x^2} – 4x + 3} \right)\).
   
   

   Câu hỏi:
   

   Tìm tập xác định \(D\) của hàm số \(y = {\log _3}\left( {{x^2} – 4x + 3} \right)\).

   A.\(D = \left( {1;3} \right)\)

   B.\(D = \left( { – \infty ;1} \right) \cup \left( {3; + \infty } \right)\)

   Đáp án chính xác

   C.\(D = \left( { – \infty ;2 – \sqrt 2 } \right) \cup \left( {2 + \sqrt 2 ; + \infty } \right)\).

   D.\(D = \left( {2 – \sqrt 2 ;1} \right) \cup \left( {3;2 + \sqrt 2 } \right)\)

   Trả lời:

   Hàm số xác định
   \( \Leftrightarrow {x^2} – 4x + 3 >0 \Leftrightarrow \left[ \begin{array}{l}x < 1\\x >3\end{array} \right..\)</>
   Vậy \(D = \left( { – \infty ;1} \right) \cup \left( {3; + \infty } \right).\)
   Đáp án B

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Hình đa diện trong hình vẽ bên có bao nhiêu mặt?
   
   

   Câu hỏi:
   

   Hình đa diện trong hình vẽ bên có bao nhiêu mặt?
   

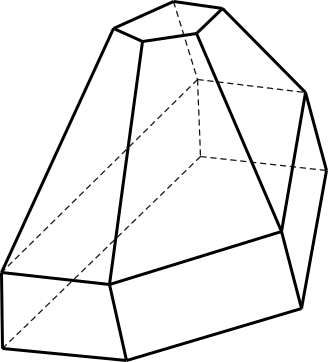
   A.6.

   B.12.

   Đáp án chính xác

   C.11.

   D.10.

   Trả lời:

   Từ hình vẽ, ta thấy hình đa diện trên có 12 mặt.
   Đáp án B

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====