Cho hàm số \(f\left( x \right) = \left| {3{{\rm{x}}^4} – 4{{\rm{x}}^3} – 12{{\rm{x}}^2} + m} \right|\). Gọi M là giá trị lớn nhất của hàm số \(f\left( x \right)\) trên đoạn \(\left[ { – 1;3} \right]\). Giá trị nhỏ nhất của M bằng

Câu hỏi:

Cho hàm số \(f\left( x \right) = \left| {3{{\rm{x}}^4} – 4{{\rm{x}}^3} – 12{{\rm{x}}^2} + m} \right|\). Gọi M là giá trị lớn nhất của hàm số \(f\left( x \right)\) trên đoạn \(\left[ { – 1;3} \right]\). Giá trị nhỏ nhất của M bằng

A. \(\frac{{59}}{2}\)   

Đáp án chính xác

B. \(\frac{5}{2}\)        

C. 16                         

D. \(\frac{{57}}{2}\)

Trả lời:

Đáp án A
Đặt \(g\left( x \right) = 3{{\rm{x}}^4} – 4{{\rm{x}}^3} – 12{{\rm{x}}^2} + m\).
Có $g^{‘}\left(x\right)=12{\text{x}}^3-12{\text{x}}^2-24\text{x};\left(x\right)=0\iff \left[\begin{array}{l}x=-1\\ x=0\\ x=2\end{array}\right.$
Ta có: \(g\left( { – 1} \right) = m – 5;{\rm{ g}}\left( 0 \right) = m;{\rm{ g}}\left( 2 \right) = m – 32;{\rm{ g}}\left( 3 \right) = m + 27\).
Ta thấy: \(m – 32 < m – 5 < m < m + 27,\forall m\).
TH1: Nếu \$m-32<m+27\le 0\iff m\le -27$ thì \(M = \left| {m – 32} \right|\) và \(\min M = 59\).
TH2: \(\left\{ {\begin{array}{*{20}{l}}{m – 32 < 0 < m + 27}\\{\left| {m – 32} \right| \le \left| {m + 27} \right|}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{ – 27 < m < 32}\\{ – m – 27 \le m – 32 \le m + 27}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{ – 27 < m < 32}\\{m \ge \frac{5}{2}}\end{array}} \right. \Leftrightarrow \frac{5}{2} \le m < 32\) thì \(M = \left| {m + 27} \right|\) và \(\min M = \frac{{59}}{2}\).
TH3: $\left\{\begin{array}{l}m-32<0<m+27\\ \left|m+27\right|\le \left|m-32\right|\end{array}\right.\iff \left\{\begin{array}{l}-27<m<32\\ m-32\le m+27\le -m+32\end{array}\right.\iff \left\{\begin{array}{l}-27<m<32\\ m\le \frac{5}{2}\end{array}\right.\iff -27<m\le \frac{5}{2}$ thì $M=\left|m-32\right|$ và $\min M=\frac{59}{2}$
TH4: Nếu \(0 \le m – 32 < m + 27 \Leftrightarrow m \ge 32\) thì \(M = \left| {m + 27} \right|\) và \(\min M = 59\).
Vậy \(\min M = \frac{{59}}{2}\) khi \(m = \frac{5}{2}\).

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Trong không gian tọa độ Oxyz, phương trình chính tắc của đường thẳng đi qua điểm \(A\left( {1; – 1;2} \right)\) và có vectơ chỉ phương \(\overrightarrow u \left( {2; – 1;3} \right)\) là
   
   

   Câu hỏi:
   

   Trong không gian tọa độ Oxyz, phương trình chính tắc của đường thẳng đi qua điểm \(A\left( {1; – 1;2} \right)\) và có vectơ chỉ phương \(\overrightarrow u \left( {2; – 1;3} \right)\) là

   A. \(\frac{{x + 1}}{2} = \frac{{y – 1}}{{ – 1}} = \frac{{z + 2}}{3}\) 

   B. \(\frac{{x – 2}}{1} = \frac{{y + 1}}{{ – 1}} = \frac{{z – 3}}{2}\)       

   C. \(\frac{{x + 2}}{1} = \frac{{y – 1}}{{ – 1}} = \frac{{z + 3}}{2}\)        

   D. \(\frac{{x – 1}}{2} = \frac{{y + 1}}{{ – 1}} = \frac{{z – 2}}{3}\)

   Đáp án chính xác

   Trả lời:

   Đáp án D
   Ta có \(d:\frac{{x – 1}}{2} = \frac{{y + 1}}{{ – 1}} = \frac{{z – 2}}{3}\).

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Đường cong trong hình vẽ là đồ thị của hàm số nào dưới đây
   
   

   Câu hỏi:
   

   Đường cong trong hình vẽ là đồ thị của hàm số nào dưới đây
   

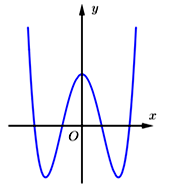
   A. \(y = {x^4} – 4{{\rm{x}}^2} + 2\)

   Đáp án chính xác

   B. \(y = {x^4} + 4{{\rm{x}}^2} + 2\)

   C. $y=-x^4+4{\text{x}}^2+2$

   D. \(y = {x^3} – 4{{\rm{x}}^2} + 2\)

   Trả lời:

   Đáp án A
   Ta loại ngay D. Từ $\lim x\to -\infty y=\lim x\to +\infty y=+\infty \Rightarrow$ Hệ số \(a > 0 \Rightarrow \) Loại C.
   Hàm số có 3 điểm cực trị nên \(ab < 0 \Rightarrow \) Loại B.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Cho tập hợp \(A = \left\{ {1;2;3;4;5} \right\}\). Hỏi có bao nhiêu số có 3 chữ số (không nhất thiết khác nhau) được lập từ các số thuộc tập hợp A  
   
   

   Câu hỏi:
   

   Cho tập hợp \(A = \left\{ {1;2;3;4;5} \right\}\). Hỏi có bao nhiêu số có 3 chữ số (không nhất thiết khác nhau) được lập từ các số thuộc tập hợp A  

   A. \({5^3}\)                

   Đáp án chính xác

   B. \({3^5}\)                

   C. \(C_5^3\)              

   D. \(A_5^3\)

   Trả lời:

   Đáp án A
   Số cần lập có dạng \(\overline {abc} {\rm{ }}\left( {a,b,c \in {\rm{A}}} \right)\).
   Vì a, b, c không nhất thiết khác nhau nên a, b, c đều có 5 cách chọn.
   Do đó \(5.5.5 = {5^3}\) số thỏa mãn yêu cầu bài toán.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Cho \∫02fxdx=3 và ∫02gxdx=7, khi đó ∫02fx+3gxdx bằng
   
   

   Câu hỏi:
   

   Cho \$\underset{0}{\overset{2}{\int }}f\left(x\right)d\text{x}=3$ và $\underset{0}{\overset{2}{\int }}g\left(x\right)dx=7$, khi đó $\underset{0}{\overset{2}{\int }}\left[f\left(x\right)+3g\left(x\right)\right]d\text{x}$ bằng

   A. 16                         

   B. \( – 18\)                 

   C. 24                         

   Đáp án chính xác

   D. 10

   Trả lời:

   Đáp án C
   Ta có   $I=\underset{0}{\overset{2}{\int }}f\left(x\right)d\text{x}+3\underset{0}{\overset{2}{\int }}g\left(x\right)d\text{x}=3+3.7=24$

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Tập nghiệm của bất phương trình \({2^{{x^2} + 2{\rm{x}}}} \le 8\) là
   
   

   Câu hỏi:
   

   Tập nghiệm của bất phương trình \({2^{{x^2} + 2{\rm{x}}}} \le 8\) là

   A. \(\left( { – \infty ; – 3} \right]\)                 

   B. \(\left[ { – 3;1} \right]\)      

   Đáp án chính xác

   C. \(\left( { – 3;1} \right)\)                        

   D. \(\left( { – 3;1} \right]\)

   Trả lời:

    Đáp án B
   BPT $\iff 2^{x^2+2\text{x}}\le 2^3\iff x^2+2\text{x}\le 3\iff -3\le x\le 1$

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====