Cho hai số thực dương m,n(n≠1) thỏa mãn log7m.log27log210−1=3+1logn5 . Khẳng định nào sau đây là đúng?

Câu hỏi:

Cho hai số thực dương $m,n(n\ne 1)$ thỏa mãn $\frac{{\log }_{7}m.{\log }_{2}7}{{\log }_{2}10-1}=3+\frac{1}{{\log }_{n}5}$ . Khẳng định nào sau đây là đúng?

A.$m=15n$

B.$m=25n$

C.$m=125n$

Đáp án chính xác

D.$m.n=125$

Trả lời:

Phương pháp giải:
Sử dụng các công thức: ${\log }_{a}b.{\log }_{b}c={\log }_{a}c(0<a,b\ne \mathrm{1,}c>0)$; ${\log }_{a}x-{\log }_{a}y={\log }_a\frac{x}{y}(0<a\ne \mathrm{1,}x,y>0)$
Giải chi tiết:
Ta có: $\frac{{\log }_{7}m.{\log }_{2}7}{{\log }_{2}10-1}=3+\frac{1}{{\log }_{n}5}$
$\iff \frac{{\log }_{2}7.{\log }_{7}m}{{\log }_{2}10-{\log }_{2}2}=3+\frac{1}{{\log }_{n}5}$
$\iff \frac{{\log }_{2}m}{{\log }_{2}5}=3+\frac{1}{{\log }_{n}5}$
$\iff \frac{{\log }_{2}m}{{\log }_{2}5}=\frac{3{\log }_{n}5+1}{{\log }_{n}5}$
Đồng nhất hệ số ta có:
$\{\begin{array}{l}n=2\\ {\log }_{2}m=3{\log }_{n}5+1\end{array}\iff \{\begin{array}{l}n=2\\ {\log }_{2}m=3{\log }_{2}5+1\end{array}$
$\iff \{\begin{array}{l}n=2\\ {\log }_{2}m={\log }_{2}125+{\log }_{2}2\end{array}\iff \{\begin{array}{l}n=2\\ m=125.2=125n\end{array}$
Vậy $m=125n$.
Đáp án C

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Tập xác định D của hàm số y=2020sinx  là:
   
   

   Câu hỏi:
   

   Tập xác định $D$ của hàm số $y=\frac{2020}{\sin x}$  là:

   A.$D=ℝ$

   B.$D=ℝ\backslash \left\{0\right\}$

   C.$D=ℝ\backslash \{\frac{\pi }{2}+k\pi ,k\in \mathbb{Z}\}$

   D.$D=ℝ\backslash \{k\pi ;k\in \mathbb{Z}\}$

   Đáp án chính xác

   Trả lời:

   Phương pháp giải:
   – Hàm số $y=\sin x$ xác định với mọi $x\in ℝ$.
   – Hàm phân thức xác định khi mẫu thức khác 0.
   Giải chi tiết:
   Hàm số $y=\frac{2020}{\sin x}$ xác định khi và chỉ khi $\sin x\ne 0\iff x\ne k\pi (k\in \mathbb{Z})$.
   Vậy TXĐ của hàm số là $D=ℝ\backslash \{k\pi ;k\in \mathbb{Z}\}$.
   Đáp án D

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Tìm hệ số của x12 trong khai triển (2x−x2)10 .
   
   

   Câu hỏi:
   

   Tìm hệ số của $x^{12}$ trong khai triển ${(2x-x^2)}^{10}$ .

   A.$C_{10}^8$

   B.$C_{10}^2{.2}^8$

   Đáp án chính xác

   C.$C_{10}^2$

   D.$-C_{10}^2{.2}^8$

   Trả lời:

   Phương pháp giải:
   – Khai triển nhị thức Niu-tơn ${(a+b)}^n=\sum _{k=0}^n{C}_n^k{a}^k{b}^{n-k}$.
   – Tìm hệ số của số hạng chứa $x^{12}$ trong khai triển.
   Giải chi tiết:
   Ta có: ${(2x-x^2)}^{10}=\sum _{k=0}^{10}{C}_{10}^k{\left(2x\right)}^{10-k}{(-x^2)}^k=\sum _{k=0}^{10}{C}_{10}^k{(-1)}^k{2}^{10-k}{x}^{10+k}$.
   Khi đó để tìm hệ số của số hạng chứa $x^{12}$, ta cho $10+k=12\iff k=2\left(tm\right)$.
   Vậy hệ số của số hạng chứa $x^{12}{x}^{12}$ trong khai triển trên là $C_{10}^2{(-1)}^2{.2}^8=2^8{C}_{10}^2$.
   Đáp án B

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Cho hình chóp S.ABCD có đáy ABCD  là hình chữ nhật với AD=a,AB=2a . Cạnh bên SA vuông góc với đáy. Gọi M,N lần lượt là trung điểm của SB và SD. Tính khoảng cách d từ S đến mặt phẳng (AMN) .
   
   

   Câu hỏi:
   

   Cho hình chóp $S.ABCD$ có đáy $ABCD$  là hình chữ nhật với $AD=a,AB=2a$ . Cạnh bên SA vuông góc với đáy. Gọi M,N lần lượt là trung điểm của SB và SD. Tính khoảng cách d từ S đến mặt phẳng $\left(AMN\right)$ .

   A.$d=\frac{a\sqrt{6}}{3}$

   Đáp án chính xác

   B.$d=2a$

   C.$d=\frac{3a}{2}$

   D.$d=a\sqrt{5}$

   Trả lời:

   Phương pháp giải:
   – Tính thể tích chóp $S.ABCD$, sử dụng tỉ lệ thể tích Simpson tính thể tích khối chóp $V_{S.AMN}$.
   – Sử dụng công thức
   $S_{AMN}=\sqrt{p(p-AM)(p-AN)(p-MN)}$ với p là nửa chu vi $\Delta AMN$.
   Giải chi tiết:
   
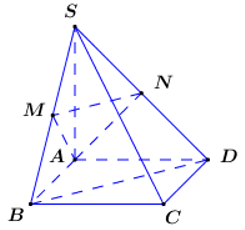
   Áp dụng định lí Pytago trong các tam giác vuông $SAB,SAD,ABD$ ta có:
   $SB=\sqrt{S{A}^2+A{B}^2}=\sqrt{4a^2+4a^2}=2\sqrt{2}a$
   $SD=\sqrt{S{A}^2+A{D}^2}=\sqrt{4a^2+a^2}=\sqrt{5}a$
   $BD=\sqrt{A{B}^2+A{D}^2}=\sqrt{4a^2+a^2}=\sqrt{5}a$
   Khi đó ta có $AM=\frac{1}{2}SB=\sqrt{2}a;AN=\frac{1}{2}SD=\frac{a\sqrt{5}}{2}$ (đường trung tuyến trong tam giác vuông).
   Ta có: MN là đường trung bình của $\Delta SBD$ nên $MN=\frac{BD}{2}=\frac{a\sqrt{5}}{2}$.
   Gọi p là nửa chu vi tam giác $AMN$ ta có: $p=\frac{AM+AN+MN}{2}=\frac{\sqrt{2}a+\frac{a\sqrt{5}}{2}+\frac{a\sqrt{5}}{2}}{2}=\frac{\sqrt{2}+\sqrt{5}}{2}a$.
   ⇒ Diện tích tam giác $AMN$ là $S_{AMN}=\sqrt{p(p-AM)(p-AN)(p-MN)}=\frac{a^2\sqrt{6}}{4}$
   Ta có: $\frac{V_{S.AMN}}{V_{S.ABD}}=\frac{SM}{SB}.\frac{SN}{SD}=\frac{1}{4}$ $\Rightarrow V_{S.AMN}=\frac{1}{4}{V}_{S.ABD}=\frac{1}{8}{V}_{S.ABCD}$.
   Mà $V_{S.ABCD}=\frac{1}{3}SA.S_{ABCD}=\frac{1}{3}.2a.2a.a=\frac{4a^3}{3}$ $\Rightarrow V_{S.AMN}=\frac{1}{8}.\frac{4a^3}{3}=\frac{a^3}{6}$.
   Lại có $V_{S.AMN}=\frac{1}{3}d(S;\left(AMN\right)).S_{AMN}$, do đó $d(S;\left(AMN\right))=\frac{3V_{S.AMN}}{S_{AMN}}=\frac{3.\frac{a^3}{6}}{\frac{a^2\sqrt{6}}{4}}=\frac{a\sqrt{6}}{3}$.
   Vậy $d(S;\left(AMN\right))=\frac{a\sqrt{6}}{3}$
   Đáp án A.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Tìm giá trị lớn nhất của hàm số f(x)=x3−3×2−4x+1 trên đoạn [1;3] .
   
   

   Câu hỏi:
   

   Tìm giá trị lớn nhất của hàm số $f\left(x\right)=x^3-3x^2-4x+1$ trên đoạn $[1;3]$ .

   A.$\underset{[1;3]}{\max }f\left(x\right)=-7$

   B.$\underset{[1;3]}{\max }f\left(x\right)=-4$

   C.$\underset{[1;3]}{\max }f\left(x\right)=-2$

   Đáp án chính xác

   D.$\underset{[1;3]}{\max }f\left(x\right)=\frac{67}{27}$

   Trả lời:

   Phương pháp giải:
   Sử dụng MTCT, chức năng MODE 7.
   Giải chi tiết:
   Sử dụng MODE 7, nhập $f\left(X\right)=X^3-2X^2-4X+1$, chọn Start = 1, End = 3, Step = 0,1.
   Do cột $F\left(X\right)$:
   
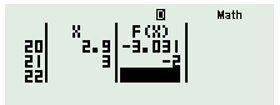
   Vậy $\underset{[1;3]}{\max }f\left(x\right)=-2$.
   Đáp án C

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Nếu các số 5+m, 7+2m, 17+m theo thứ tự lập thành cấp số cộng thì m bằng bao nhiêu?
   
   

   Câu hỏi:
   

   Nếu các số $5+m$, $7+2m$, $17+m$ theo thứ tự lập thành cấp số cộng thì m bằng bao nhiêu?

   A.$m=2$

   B.$m=3$

   C.$m=4$

   Đáp án chính xác

   D.$m=5$

   Trả lời:

   Phương pháp giải:
   Sử dụng tính chất của cấp số cộng: Nếu ba số $a,b,c$ lần lượt lập thành một cấp số cộng thì $a+c=2b$.
   Giải chi tiết:
   Vì $5+m\mathrm{,7}+2m\mathrm{,17}+m$ theo thứ tự lập thành cấp số cộng nên ta có:
   $5+m+17+m=2(7+2m)\iff 2m+22=4m+14\iff m=4$
   Đáp án C

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====