30 câu Trắc nghiệm Tích phân có đáp án 2023 – Toán 12

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây

Bài tập trắc nghiệm tích phân có đáp án và lời giải chi tiết

Tích phân

A. Kiến thức cơ bản

1.Định nghĩa

Cho f là hàm số liên tục trên đoạn [a ; b]. Giả sử F là một nguyên hàm của f trên [a ; b]. Hiệu số F(b)-F(a) được gọi là tích phân từ a đến b (hay tích phân xác định trên đoạn [a ; b] của hàm số f(x), kí hiệu là \(\int_a^b f (x)dx\).

Ta dùng kí hiệu \(\left. {F(x)} \right|_a^b = F(b) – F(a)\) để chỉ hiệu số \(F(b) – F(a)\). Vậy \(\int_a^b f (x)dx = \left. {F(x)} \right|_a^b = F(b) – F(a).\)

Nhận xét: Tích phân của hàm số f từ a đến b có thể kí hiệu bởi \(\int_a^b f (x)dx\) hay \(\int_a^b f (t)dt\). Tích phân đó chỉ phụ thuộc vào f và các cận a, b mà không phụ thuộc vào cách ghi biến số.

Ý nghĩa hình học của tích phân: Nếu hàm số f liên tục và không âm trên đoạn [a ; b] thì tích phân \(\int_a^b f (x)dx\) là diện tích S của hình thang cong giới hạn bởi đồ thị hàm số y = f(x), trục Ox và hai đường thẳng x = a; x = b. Vậy \(S = \int_a^b f (x)dx\).

2.Tính chất của tích phân

1. \(\int_a^a f (x)dx = 0\)

2. \(\int_a^b f (x)dx =  – \int_b^a f (x)dx\)

3. \(\int_a^b f (x)dx + \int_b^c f (x)dx = \int_a^c f (x)dx(a < b < c)\)

4. \(\int_a^b k  \cdot f(x)dx = k \cdot \int_a^b f (x)dx(k \in \mathbb{R})\)

5.${\int }_a^b\left[f\right(x)\pm g(x\left)\right]dx={\int }_a^{b}f\left(x\right)dx\pm {\int }_a^{b}g\left(x\right)dx.$

B. Bài tập

Áp dụng định nghĩa, tính chất và bảng nguyên hàm

Câu 1: Cho hàm số y = f(x), y = g(x) liên tục trên [a ; b] và số thực k tùy ý. Trong các khẳng định sau, khẳng định nào sai?

A. \(\int_a^b f (x){\rm{d}}x =  – \int_b^a f (x){\rm{d}}x\).

B. \(\int_a^b x f(x){\rm{d}}x = x\int_a^b f (x){\rm{d}}x\).

C. \(\int_a^a k f(x){\rm{d}}x = 0\).

D. ${\int }_a^b\left[f\right(x)+g(x\left)\right]\text{d}x={\int }_a^{b}f\left(x\right)\text{d}x+{\int }_a^{b}g\left(x\right)\text{d}x$ .

Câu 2: Khẳng định nào sau đây sai?

A.  ${\int }_a^b\left[f\right(x)+g(x\left)\right]\text{d}x={\int }_a^{b}f\left(x\right)\text{d}x+{\int }_a^{b}g\left(x\right)\text{d}x\text{. }$

B. \(\int_a^b f (x){\rm{d}}x = \int_c^b f (x){\rm{d}}x + \int_a^c f (x){\rm{d}}x\).

C. \(\int_a^b f (x){\rm{d}}x = \int_b^a f (x){\rm{d}}x\)

D. \(\int_a^b f (x){\rm{d}}x = \int_a^b f (t){\rm{d}}t\).

Câu 3: Cho hai hàm số f(x) và g(x) liên tục trên \(K,a,b \in K\). Khẳng định nào sau đây là khẳng định sai?

A.${\int }_a^b\left[f\right(x)+g(x\left)\right]\text{d}x={\int }_a^{b}f\left(x\right)\text{d}x+{\int }_a^{b}g\left(x\right)\text{d}x$

B. \(\int_a^b k f(x){\rm{d}}x = k\int_a^b f (x){\rm{d}}x\).

C. \(\int_a^b f (x)g(x){\rm{d}}x = \int_a^b f (x){\rm{d}}x \cdot \int_a^b g (x){\rm{d}}x.\)

D.${\int }_a^b\left[f\right(x)-g(x\left)\right]\text{d}x={\int }_a^{b}f\left(x\right)\text{d}x-{\int }_a^{b}g\left(x\right)\text{d}x$

Câu 4: Cho hai số thực a, b tùy ý, F(x) là một nguyên hàm của hàm số f(x) trên tập \(\mathbb{R}\). Mệnh đề nào dưới đây là đúng?

A. \(\int_a^b f (x){\rm{d}}x = f(b) – f(a)\).

B. \(\int_a^b f (x){\rm{d}}x = F(b) – F(a)\).

C. \(\int_a^b f (x){\rm{d}}x = F(a) – F(b)\).

D. \(\int_a^b f (x){\rm{d}}x = F(b) + F(a)\).

Câu 5: Cho f(x) là hàm số liên tục trên đoạn [a ; b] và \(c \in [a;b]\). Tìm mệnh đề đúng trong các mệnh đề sau.

A. \(\int_a^c f (x){\rm{d}}x + \int_c^b f (x){\rm{d}}x = \int_b^a f (x){\rm{d}}x\).

B. \(\int_a^b f (x){\rm{d}}x + \int_a^c f (x){\rm{d}}x = \int_c^b f (x){\rm{d}}x\).

C. \(\int_a^b f (x){\rm{d}}x – \int_a^c f (x){\rm{d}}x = \int_c^c f (x){\rm{d}}x\).

D. \(\int_a^b f (x){\rm{d}}x + \int_c^a f (x){\rm{d}}x = \int_c^b f (x){\rm{d}}x\).

Câu 6: Cho hàm số y = f(x) liên tục trên khoảng K và \(a,b,c \in K\). Mệnh đề nào sau đây sai?

A. \(\int_a^b f (x){\rm{d}}x + \int_c^b f (x){\rm{d}}x = \int_a^c f (x){\rm{d}}x\).

B. \(\int_a^b f (x){\rm{d}}x = \int_a^b f (t){\rm{dt}}\).

C. \(\int_a^b f (x){\rm{d}}x =  – \int_b^a f (x){\rm{d}}x\).

D. \(\int_a^a f (x){\rm{d}}x = 0\).

Câu 7: Cho hàm số f(t) liên tục trên K và \(a,b \in K,F(t)\) là một nguyên hàm của f(t) trên K. Chọn khẳng định sai trong các khẳng định sau.

A. \(F(a) – F(b) = \int_a^b f (t){\rm{d}}t\).

B. \(\int_a^b f (t){\rm{d}}t = \left. {F(t)} \right|_a^b\).

C. \(\int_a^b f (t){\rm{d}}t = \left. {\left( {\int f (t){\rm{d}}t} \right)} \right|_a^b\).

D. \(\int_a^b f (x){\rm{d}}x = \int_a^b f (t){\rm{d}}t\).

Câu 8: Cho hàm số y = f(x) liên tục trên đoạn [a ; b]. Mệnh đề nào dưới đây sai?

A. \(\int_a^b f (x){\rm{d}}x = \int_a^b f (t){\rm{d}}t.\)

B. \(\int_a^b f (x){\rm{d}}x =  – \int_b^a f (x){\rm{d}}x\).

C. \(\int_a^b k \;{\rm{d}}x = k(a – b),\forall k \in \mathbb{R}\).

D. \(\int_a^b f (x){\rm{d}}x = \int_a^c f (x){\rm{d}}x + \int_c^b f (x){\rm{d}}x,\forall c \in (a;b)\).

Câu 9: Giả sử f là hàm số liên tục trên khoảng K và a, b, c là ba số bất kỳ trên khoảng K. Khẳng định nào sau đây sai?

A. \(\int_a^a f (x)dx = 1\).

B. \(\int_a^b f (x)dx =  – \int_b^a f (x)dx\).

C. \(\int_a^c f (x)dx + \int_c^b f (x)dx = \int_a^b f (x)dx,c \in (a;b)\).

D. \(\int_a^b f (x)dx = \int_a^b f (t)dt\).

Câu 10: Cho hàm số y = f(x) liên tục trên đoạn [a ; b]. Mệnh đề nào dưới đây sai?

A. \(\int_a^b f (x){\rm{d}}x =  – \int_b^a f (x){\rm{d}}x\).

B. \(\quad \int_a^b f (x){\rm{d}}x = \int_a^c f (x){\rm{d}}x + \int_c^b f (x){\rm{d}}x\), \(\forall c \in \mathbb{R}\).

C. \(\int_a^b f (x){\rm{d}}x = \int_a^b f (t){\rm{d}}t\).

D. \(\int_a^a f (x){\rm{d}}x = 0\).

Câu 11: Cho F(x) là một nguyên hàm của hàm số f(x). Khi đó hiệu số F(0) – F(1) bằng

A. \(\int_0^1 f (x){\rm{d}}x\).

B. \(\int_0^1  –  F(x){\rm{d}}x\).

C. \(\int_0^1  –  F(x){\rm{d}}x\).

D. \(\int_0^1  –  f(x){\rm{d}}x\).

Câu 12: Cho hàm số y = f(x) liên tục trên [a ; b], có đồ thị \(y = {f^\prime }(x)\) như hình vẽ sau:

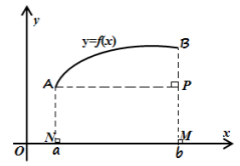
Mệnh đề nào dưới đây đúng?

A. \(\int_a^b {{f^\prime }} (x){\rm{d}}x\) là diện tích hình thang ABMN.

B. \(\int_a^b {{f^\prime }} (x){\rm{d}}x\) là dộ dài đoạn BP.

C. \(\int_a^b {{f^\prime }} (x){\rm{d}}x\) là dộ dài đoạn MN.

D. \(\int_a^b {{f^\prime }} (x){\rm{d}}x\) là dộ dài đoạn cong AB.

Câu 13: Cho hai tích phân \(\int_{ – a}^a f (x)dx = m\) và \(\int_{ – a}^a g (x)dx = n\). Giá trị của tích phân  là:

A. m – n.

B. n – m.

C. m + n.

D. Không thể xác định.

Câu 14: Cho tích phân \({I_1} = \int_a^b f (x)dx = m\) và \({I_2} = \int_c^a f (x)dx = n\). Tích phân \(I = \int_c^b f (x)dx\) có giá trị là:

A. m + n.

B. m – n.

C. – m – n.

D. Không thể xác định.

Câu 15: Tích phân \(\int_a^b f (x)dx\) được phân tích thành:

A. \(\int_c^b f (x) + \int_c^a  –  f(x)dx\).

B. \(\int_c^b f (x) – \int_c^a  –  f(x)dx\).

C. \(\int_c^b f (x) + \int_c^a f (x)dx\).

D. \( – \int_c^b f (x) + \int_c^a f (x)dx\).

Câu 16: Cho \(\int_{ – 2}^1 f (x){\rm{d}}x = 3\). Tính tích phân  .

A. – 9.

B. – 3.

C. 3 .

D. 5 .

Câu 17: Cho hàm f(x) có đạo hàm liên tục trên [2 ; 3] đồng thời f(2) = 2, f(3) = 5. Tính \(\int_2^3 {{f^\prime }} (x){\rm{d}}x\) bằng

A. -3.

B. 7 .

C. 10

D. 3 .

Câu 18: Cho \(\int_a^b {{f^\prime }} (x){\rm{d}}x = 7\) và \(f(b) = 5\). Khi đó f(a) bằng

A. 12 .

B. 0 .

C. 2 .

D. – 2.

Câu 19: Cho hàm số f(x) có đạo hàm liên tục trên đoạn [a ; b] và f(a) = -2, f(b) = -4. Tính \(T = \int_a^b {{f^\prime }} (x){\rm{d}}x.\)

A. T = -6.

B. T = 2.

C. T = 6.

D. T = -2.

Câu 20: Cho hàm số f(x) liên tục trên [0 ; 1] và f(1) – f(0) =2. Tính tích phân \(\int_0^1 {{f^\prime }} (x){\rm{d}}x\).

A. I = -1.

B. I = 1.

C. I = 2.

D. I = 0.

Câu 21: Cho hàm số y = f(x) thoả mãn điều kiện \(f(1) = 12,{f^\prime }(x)\) liên tục trên \(\mathbb{R}\) và \(\int_1^4 {{f^\prime }} (x){\rm{d}}x = 17\) . Khi đó f(4) bằng

A. 5 .

B. 29 .

C. 19 .

D. 9 .

Câu 22: Cho hàm số f(x) có đạo hàm liên tục trên đoạn [-1 ; 3] và thỏa mãn f(-1) =4 ; f(3) =7 . Giá trị của \(I = \int_{ – 1}^3 5 {f^\prime }(x){\rm{d}}x\) bằng

A. I = 20.

B. I = 3.

C. I = 10.

D. I =15.

Câu 23: Cho hàm số \(f(x) = \frac{a}{{{x^2}}} + \frac{b}{x} + 2\), với a, b là các số hữu tỉ thỏa điều kiện \(\int_{\frac{1}{2}}^1 f (x){\rm{d}}x = 2 – 3\ln 2\). Tính T = a + b.

A. T = -1.

B. T = 2.

C. T = -2.

D. T = 0

Câu 24: Tính tích phân \(I = \int_0^3 {\frac{{{\rm{d}}x}}{{x + 2}}} \).

A. \(I = \frac{{4581}}{{5000}}\).

B. \(I = \log \frac{5}{2}\).

C. \(I = \ln \frac{5}{2}\).

D. \(I =  – \frac{{21}}{{100}}\).

Câu 25: Tính tích phân \(I = \int_1^{{2^{2018}}} {\frac{{{\rm{d}}x}}{x}} \).

A. I = 2018. ln 2 -1.

B. \(I = {2^{2018}}\).

C. I = 2018. ln 2.

C. I = 2018.

Câu 26: Tính \(I = \int_0^1 {\left( {\frac{1}{{2x + 1}} + 3\sqrt x } \right)} {\rm{d}}x\).

A. \(2 + \ln \sqrt 3 \).

B. 4 + ln 3.

C. 2 + ln 3.

D. \(1 + \ln \sqrt 3 \).

Câu 27:

Tính tích phân \(I = \int_0^1 {{x^{2018}}} (1 + x){\rm{d}}x\)

A. \(I = \frac{1}{{2018}} + \frac{1}{{2019}}\).

B. \(I = \frac{1}{{2020}} + \frac{1}{{2021}}\).

C. \(I = \frac{1}{{2019}} + \frac{1}{{2020}}\).

D. \(I = \frac{1}{{2017}} + \frac{1}{{2018}}\)

Câu 28: Cho hàm số $y=f\left(x\right)=\left\{\begin{array}{l}3x^2\\ 4-x\end{array}\right.$$\begin{array}{l}\text{ khi }0\le x\le 1\\ \text{ khi }1\le x\le 2\end{array}$. Tính tích phân \(\int_0^2 f (x){\rm{d}}x\).

A. \(\frac{7}{2}\).

B. 1 .

C. \(\frac{5}{2}\).

D. \(\frac{3}{2}\).

Câu 29: Cho hàm số $y=f\left(x\right)=\left\{\begin{array}{l}\frac{2}{x+1}\\ 2x-1\end{array}\right.$$\begin{array}{l}\text{ khi }\\ \text{ khi }\end{array}$$\begin{array}{l}0\le x\le 1\\ 1\le x\le 3\end{array}$. Tính tích phân \(\int_0^3 f (x){\rm{d}}x\).

A. 6 + ln 4.

B. 4 + ln 4.

C. 6 + ln 2.

D. 2 +2 ln 2.