Cho một hình nón có thiết diện qua trục là một tam giác đều cạnh bằng 1. Tính thể tích khối càu nội tiếp trong hình nón.

Câu hỏi:

Cho một hình nón có thiết diện qua trục là một tam giác đều cạnh bằng 1. Tính thể tích khối càu nội tiếp trong hình nón.

A.$\frac{\pi }{6}$

B.$\frac{4\sqrt{3}\pi }{27}$

Đáp án chính xác

C.$\frac{4\pi }{81}$

D.$\frac{\sqrt{3}\pi }{54}$

Trả lời:

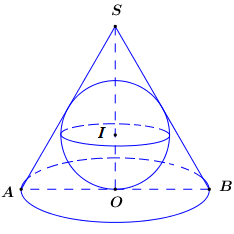
Giả sử thiết diện qua trục là tam giác SAB và O là tâm mặt đáy của hình nón, ta có tam giác SAB đều cạnh 1 nên $SO=\frac{\sqrt{3}}{2}$.
Gọi I là tâm khối cầu nội tiếp trong hình nón, dễ thấy O chính là tâm tam giác đều SAB, do đó bán kính khối cầu là $R=IO=\frac{2}{3}SO=\frac{2}{3}.\frac{\sqrt{3}}{2}=\frac{\sqrt{3}}{3}$.
Vậy thể tích khối cầu nội tiếp trong hình nón là $V=\frac{4}{3}\pi R^3=\frac{4}{3}\pi {\left(\frac{\sqrt{3}}{3}\right)}^3=\frac{4\sqrt{3}\pi }{27}$.
Đáp án B.

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Hàm số nào sau đây có đồ thị như hình vẽ bên dưới?
   
   

   Câu hỏi:
   

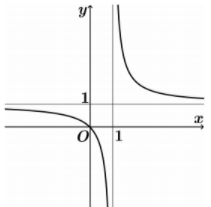
   Hàm số nào sau đây có đồ thị như hình vẽ bên dưới?
   

   A.$y=\frac{x}{1-x}$

   Đáp án chính xác

   B.$y=\frac{x+1}{1-x}$

   C.$y=\frac{x+1}{x-1}$

   D.$y=\frac{x}{x-1}$

   Trả lời:

   Dựa vào đồ thị hàm số ta thấy: Đồ thị có đường TCN y=1 và TCĐ x=1.
   Do đó loại đáp án A và B.
   Đồ thị hàm số đi qua điểm O(0;0) nên loại đáp án C.
   Đáp án A.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Tìm tất cả các điểm M nằm trên đồ thị hàm số y=x−2x+1 mà tiếp tuyến của đồ thị tại điểm đó song song với đường thẳng d:y=3x+10.
   
   

   Câu hỏi:
   

   Tìm tất cả các điểm M nằm trên đồ thị hàm số $y=\frac{x-2}{x+1}$ mà tiếp tuyến của đồ thị tại điểm đó song song với đường thẳng $d:y=3x+10$.

   A.$M(3;\frac{1}{4})$

   B.$M(0;-2)$ hoặc \(M\left( { – 2;4} \right)\)

   Đáp án chính xác

   C.$M(-2;4)$

   D. $M(-\frac{5}{2};3)$

   Trả lời:

   TXĐ: $D=ℝ\backslash \{-1\}$.
   Gọi $M(x_0;\frac{x_0-2}{x_0+1})(x_0\ne -1)$ thuộc đồ thị hàm số $y=\frac{x-2}{x+1}$.
   Ta có $y=\frac{x-2}{x+1}\Rightarrow y^{‘}=\frac{3}{{(x+1)}^2}$ nên tiếp tuyến của đồ thị hàm số tại $M(x_0;\frac{x_0-2}{x_0+1})$ có hệ số góc là $k=y^{‘}\left(x_0\right)=\frac{3}{{(x_0+1)}^2}$.
   Vì tiếp tuyến tại M song song với đường thẳng $d:y=3x+10$nên \(\frac{3}{{{{\left( {{x_0} + 1} \right)}^2}}} = 3 \Leftrightarrow {\left( {{x_0} + 1} \right)^2} = 1\)
   $\iff [\begin{array}{l}{x}_0+1=1\\ x_0+1=-1\end{array}\iff [\begin{array}{l}{x}_0=0\\ x_0=-2\end{array}\left(tm\right)$$\Rightarrow [\begin{array}{l}M(0;-2)\\ M(-2;4)\end{array}$
   Đáp án B.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Cho hàm số \(y = \frac{{x + 1}}{{1 – x}}\) và điểm I(1;−1). Tìm tất cả các điểm M nằm trên đồ thị hàm số sao cho tiếp tuyến tại M vuông góc với IM.
   
   

   Câu hỏi:
   

   Cho hàm số \(y = \frac{{x + 1}}{{1 – x}}\) và điểm $I(1;-1)$. Tìm tất cả các điểm M nằm trên đồ thị hàm số sao cho tiếp tuyến tại M vuông góc với IM.

   A.$M(1+\sqrt{2};-1-\sqrt{2})$ và $M(1-\sqrt{2};-1+\sqrt{2})$.

   Đáp án chính xác

   B.$M(-1;0)$ và $M(3;-2)$.

   C.$M(\sqrt{2};-3-2\sqrt{2})$ và $M(-\sqrt{2};2\sqrt{2}-3)$.

   D.$M(2;-3)$ và $M(0;1)$.

   Trả lời:

   TXĐ: $D=ℝ\backslash \left\{1\right\}$.
   Gọi $M(x_0;\frac{x_0+1}{1-x_0})(x_0\ne 1)$ thuộc đồ thị hàm số $y=\frac{x+1}{1-x}$.
   Ta có $y=\frac{x+1}{1-x}\Rightarrow y^{‘}=\frac{2}{{(1-x)}^2}$ nên tiếp tuyến của đồ thị hàm số tại $M(x_0;\frac{x_0+1}{1-x_0})$ có hệ số góc là $k=y^{‘}\left(x_0\right)=\frac{2}{{(1-x_0)}^2}$.
   ⇒ Phương trình tiếp tuyến tại M là: $y=\frac{2}{{(1-x_0)}^2}(x-x_0)+\frac{x_0+1}{1-x_0}$$\iff \frac{2}{{(1-x_0)}^2}x-y-\frac{2x_0}{{(1-x_0)}^2}+\frac{x_0+1}{1-x_0}=0$, có 1 VTCP là $\overrightarrow{u}=(1;\frac{2}{{(1-x_0)}^2})$.
   Ta có: $\overrightarrow{IM}=(x_0-1;\frac{x_0+1}{1-x_0}+1)=(x_0-1;\frac{2}{1-x_0})$.
   Vì tiếp tuyến tại M vuông góc với IM nên $\overrightarrow{u}.\overrightarrow{IM}=0$.
   \( \Leftrightarrow \left( {{x_0} – 1} \right) + \frac{4}{{{{\left( {1 – {x_0}} \right)}^3}}} = 0\)$\iff \frac{4}{{(1-x_0)}^3}=1-x_0\iff {(1-x_0)}^4=4$
   $\iff [\begin{array}{l}1-x_0=\sqrt{2}\\ 1-x_0=-\sqrt{2}\end{array}\iff [\begin{array}{l}{x}_0=1-\sqrt{2}\\ x_0=1+\sqrt{2}\end{array}$
   ⇒ $M(1+\sqrt{2};-1-\sqrt{2})$ và $M(1-\sqrt{2};-1+\sqrt{2})$.
   Đáp án A.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Mệnh đề nào dưới đây về hàm số y=(x2−4)2+1 là đúng?
   
   

   Câu hỏi:
   

   Mệnh đề nào dưới đây về hàm số $y={(x^2-4)}^2+1$ là đúng?

   A. Nghịch biến trên $(-2;2)$

   B. Đồng biến trên $ℝ$

   C. Đồng biến trên $(-\infty ;-2)$ và\(\left( {2; + \infty } \right)\)

   D. Đồng biến trên $(-2;0)$ và \(\left( {2; + \infty } \right)\).

   Đáp án chính xác

   Trả lời:

   TXĐ: $D=ℝ$.
   Ta có: $y={(x^2-4)}^2+1\Rightarrow y^{‘}=2(x^2-4).2x$.
   Cho $y^{‘}=0\iff [\begin{array}{l}x=0\\ x^2-4=0\end{array}\iff [\begin{array}{l}x=0\\ x=\pm 2\end{array}$.
   BXD y’:
   
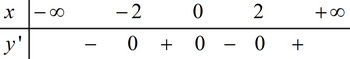
   Dựa vào BXD ta thấy hàm số đồng biến trên \(\left( { – \infty ; – 2} \right);{\mkern 1mu} {\mkern 1mu} \left( {0;2} \right)\); nghịch biến trên $(-2;0);(2;+\infty )$.
   Đáp án D.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Một người gửi tiền vào ngân hàng với lãi suát không đổi là 6% trên năm. Biết rằng nếu không rút tiền ra khỏi ngân hàng thì cứ sau mỗi năm, số tiền lãi sẽ được nhập vào vốn ban đầu (lãi kép). Người đó định gửi tiền trong vòng 3 năm, sau đó rút ra 500 triệu đồng. Hỏi số tiền ít nhất người đó phải gửi vào ngân hàng (làm tròn đến hàng triệu) là bao nhiêu triệu đồng?
   
   

   Câu hỏi:
   

   Một người gửi tiền vào ngân hàng với lãi suát không đổi là 6% trên năm. Biết rằng nếu không rút tiền ra khỏi ngân hàng thì cứ sau mỗi năm, số tiền lãi sẽ được nhập vào vốn ban đầu (lãi kép). Người đó định gửi tiền trong vòng 3 năm, sau đó rút ra 500 triệu đồng. Hỏi số tiền ít nhất người đó phải gửi vào ngân hàng (làm tròn đến hàng triệu) là bao nhiêu triệu đồng?

   A.420.

   Đáp án chính xác

   B.410.

   C.400.

   D. 390.

   Trả lời:

   Để sau 3 năm người đó rút được 500 triệu đồng thì số tiền nhận được sau 3 năm (cả gốc và lãi) phải không nhỏ hơn 500 triệu đồng.
   Gọi số tiền ban đầu gửi vào ngân hàng là x (triệu đồng), số tiền người đó nhận được sau 3 năm là: \(x{\left( {1 + 6\% } \right)^3}\) (triệu đồng).
   Khi đó ta có $x{(1+6\%)}^3\ge 500\iff x\ge 420$ (triệu đồng).
   Đáp án A.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====