Tài liệu Dạng bài tập Mặt cầu nội tiếp, ngoại tiếp hình trụ gồm các nội dung chính sau:
I. Phương pháp giải
– tóm tắt lý thuyết ngắn gọn;
II. Một số ví dụ/ Ví dụ minh họa
– gồm 9 bài toán minh họa đa dạng của các dạng bài tập trên có lời giải chi tiết.
Mời quí bạn đọc tải xuống để xem đầy đủ tài liệu Dạng bài tập Mặt cầu nội tiếp, ngoại tiếp hình trụ:
Bài giảng Toán 12: Hình trụ
NỘI NGOẠI TIẾP HÌNH TRỤ
I. Phương pháp giải
Mặt cầu ngoại tiếp hình trụ có tâm là tâm đường tròn ngoại tiếp thiết diện hình chữ nhật qua trục hình trụ.
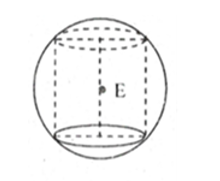
Tâm E là trung điểm trục OO’
Bán kính
– Mặt cầu nội tiếp hình trụ chỉ tồn tại khi hình trụ có đuờng kính đáy bằng chiều cao hình trụ, có tâm là tâm đường tròn nội tiếp thiết diện hình vuông qua trục hình trụ.
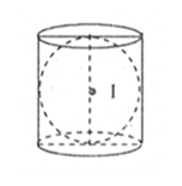
Tâm I là trung điểm của trục OO’
Bán kính r = R với điều kiện h = 2R
Chú ý:
1) Diện tích xung quanh của khối trụ: ,
Thể tích của khối trụ:
2) Diện tích mặt cầu:
Thể tích khối cầu: .
II. Ví dụ minh họa
Bài toán 1. Một khối hộp chữ nhật nội tiếp trong một khối trụ. Ba kích thước của khối hộp chữ nhật là a, b, c. Tính thế tích của khối trụ.
Giải
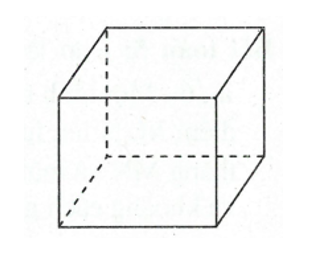
Khối hộp chữ nhật có thể nội tiếp trong ba khối trụ khác
nhau có đường tròn đáy ngoại tiếp lần lượt các mặt hình chữ
nhật, kích thước còn lại là chiều cao.
Thể tích của ba khối trụ đó lần lượt là:
và .
Bài toán 2. Mặt phẳng đi qua trục của một hình trụ, cắt hình trụ theo thiết diện là hình vuông cạnh 2R.
a) Tính diện tích xung quanh, diện tích toàn phần và thể tích của hình trụ.
b) Tính thể tích khối lăng trụ tứ giác đều nội tiếp hình trụ.
Giải
a) Từ giả thiết ta suy ra hình trụ có bán kính đáy bằng R và đường sinh bằng 2R.
Từ đó: \[{S_{xq}} = 2\pi R.2R = 4\pi {R^2}\]
![]()
\[V = \pi {R^2}.2R = 2\pi {R^3}\]
b) Hình lăng trụ tứ giác đều nội tiếp là hình tăng trụ đứng có cạnh bên bằng 2R và có đáy là hình vuông cạnh \[R\sqrt 2 \] nên có thể tích
\[{V_{LT}} = 2{R^2}.2R = 4{R^3}\].
Bài toán 3. Một khối lăng trụ tam giác đều có cạnh đáy bằng a và chiều cao bằng h nội tiếp một khối trụ. Tính thể tích của khối trụ đó.
Giải
Lăng trụ tam giác đều cạnh đáy a nên đáy hình trụ ngoại tiếp là đường tròn ngoại tiếp đáy có bán kính \[R = \frac{{a\sqrt 3 }}{3}\], chiều cao hình trụ là chiều cao h của lăng trụ.
Do đó thể tích khối trụ ngoại tiếp: \[V = \pi {R^2}h = \frac{{\pi {a^2}h}}{3}\].
Bài toán 4. Một khối lăng trụ tam giác đều có canh đáy bằng a và chiều cao bằng h ngoại tiếp một khối trụ. Tính thể tích và diện tích xung quanh của khối trụ đó.
Giải
Lăng trụ tam giác đều cạnh đáy a nên đáy hình trụ nội tiếp là đường tròn nội tiếp đáy có bán kính \[R = \frac{{a\sqrt 3 }}{6}\], chiều cao hình trụ là chiều cao h của lăng trụ.
Do đó thể tích khối trụ nội tiếp: \[V = \pi {R^2}h = \frac{{\pi {a^2}h}}{{12}}\].
Diện tích xung quanh của khối trụ \[{S_{xq}} = 2\pi Rh = \frac{{\sqrt 3 }}{3}\pi ah\].
Bài toán 5. Cho lăng trụ đều \[ABC.A’B’C’\] có cạnh đáy bằng 6a, đường cao bằng \[a\sqrt 6 \] . Một hình trụ có đáy là hai đường tròn nội tiếp tam giác ABC và \[A’B’C’\]. Hai điểm M, N lần lượt trên hai đường tròn đáy của hình trụ sao cho góc giữa đường thẳng MN và mặt đáy của hình trụ bằng \[\alpha \]. Tính thể tích khối lăng trụ \[ABC.A’B’C’\] và khoảng cách giữa đường thẳng MN và trục của hình trụ nói trên.
Giải
Ta có:
\[{V_{ABC.A’B’C’}} = {S_{ABC}}.AA’ = \frac{1}{2}6a.6a.\sin 60^\circ .a\sqrt 6 = 27{a^3}\sqrt 2 \]
Gọi r là bán kính của đường tròn nội tiếp tam giác đều ABC.
\[S = pr \Rightarrow r = \frac{{2{S_{ABC}}}}{{AB + BC + CA}} = \frac{{2{{\left( {6a} \right)}^2}\sqrt 3 }}{{4\left( {6a + 6a + 6a} \right)}} = a\sqrt 3 \].
Gọi O, \[O’\] lần lượt là tâm đường tròn nội tiếp tam giác ABC và \[A’B’C’\].
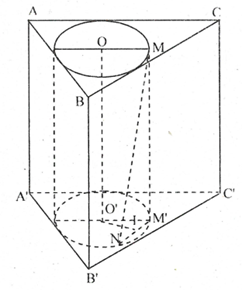
Vẽ đường sinh \[MM’\].
Gọi I là trung điểm của \[MM’\].
Khi đó \[O’I \bot M’N\]
nên \[O’I \bot \left( {MM’N} \right)\]
Do đó: \[d\left( {OO’;MM’} \right)\]
\[ = d\left( {OO’;\left( {MM’N} \right)} \right)\]
\[ = d\left( {O’;\left( {MM’N} \right)} \right) = O’I\]
Vì \[MM’ \bot \left( {A’B’C’} \right)\]
Nên góc \[\left( {MN;\left( {A’B’C’} \right)} \right) = \widehat {MNM’} = \alpha \]
Tam giác \[MM’N\] vuông tại \[M’\] ta có:
\[M’N = MM’.\cot \alpha = a\sqrt 6 .\cot \alpha \]
Tam giác \[O’M’I\] vuông tại I ta có:
\[O’I = \sqrt {{r^2} – \frac{{M{{M’}^2}}}{4}} = \sqrt {3{a^2} – \frac{{6{a^2}{{\cot }^2}\alpha }}{4}} = \frac{{a\sqrt {12 – 6{{\cot }^2}\alpha } }}{2}\]
Bài toán 6. Cho hình trụ có bán kính đáy R và chiều cao 4R. Tính thể tích mặt cầu ngoại tiếp hình trụ.
Giải
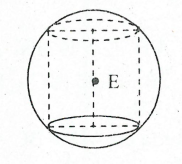
Mặt cầu ngoại tiếp hình trụ có tâm là tâm đường tròn ngoại tiếp thiết diện hình chữ nhật qua trục hình trụ.
Do đó tâm E là trung điểm trục \[OO’\].
Bán kính mặt cầu ngoại tiếp hình trụ
\[r = \sqrt {{R^2} + \frac{{{h^2}}}{4}} = \sqrt {{R^2} + 4{R^2}} = R\sqrt 5 \]
Vậy thể tích mặt cầu ngoại tiếp hình trụ.
\[V = \frac{4}{3}\pi {R^3} = \frac{{20\sqrt 5 }}{3}\pi {r^3}\].
Bài toán 7. Cho mặt cầu có bán kính R. Tính diện tích xung của hình trụ ngoại tiếp mặt cầu.
Giải
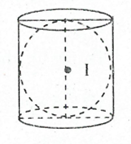
Hình trụ ngoại tiếp mặt cầu bán kính R có bán kính đáy R và chiều cao \[h = 2R\].
Vậy diện tích xung của hình trụ ngoại tiếp mặt cầu.
\[{S_{xq}} = 2\pi Rh = 4\pi {R^2}\].
Bài toán 8. Cho hình trụ T có bán kính R, trục \[OO’\] bằng 2R và mặt cầu (S) có đường kính \[OO’\].
a) So sánh diện tích mặt cầu và diện tích xung quanh của hình trụ, diện tích toàn phần của hình trụ
b) So sánh thể tích của khối trụ T và khối cầu (S).
Giải
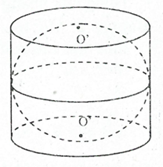
a) Diện tích của mặt cầu và diện tích xung quanh của hình trụ cùng bằng \[4\pi {R^2}\].
Diện tích toàn phần của hình trụ bằng \[4\pi {R^2} + 2\pi {R^2} = 6\pi {R^2}\]
Vậy diện tích mặt cầu bằng \[\frac{2}{3}\] diện tích toàn phần của hình trụ.
b) Thể tích của khối cầu là \[{V_{\left( S \right)}} = \frac{4}{3}\pi {R^3}\].
Thể tích của khối trụ là \[{V_T} = \pi {R^2}.2R = 2\pi {R^3}\]
Vậy thể tích của khối cầu bằng \[\frac{2}{3}\] thể tích của khối trụ.
Bài toán 9. Cho hình trụ có bán kính R và đường cao \[R\sqrt 2 \]. Gọi AB và CD là hai đường kính thay đổi của hai đường tròn đáy mà AB vuông góc với CD.
a) Chứng minh rằng ABCD là tứ diện đều.
b) Chứng minh rằng các đường thẳng AC, AD, BC, BD luôn tiếp xúc với một mặt trụ cố định.
Giải
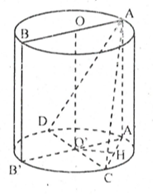
a) Gọi \[A’,B’\] lần lượt là hình chiếu của A, B trên mặt phẳng
chứa đường tròn đáy có đường kính CD, thì A, B thuộc đường
tròn này.
Khi đó \[A’B’ \bot CD\] nên \[A’CB’D\] là hình vuông có đường
chéo \[CD = 2R\], do đó \[A’C = R\sqrt 2 \], ngoài ra \[AA’ = R\sqrt 2 \] nên ta
suy ra \[AC = 2R\]
Tương tự ta có \[AD = BC = BD = 2R\].
Vậy ABCD là tứ diện đều.
b) Gọi O, \[O’\] lần lượt là trung điểm của AB và CD, H trung điểm \[A’C\].
Ta có: \[d\left( {OO’;AC} \right) = d\left( {OO’;\left( {AA’C} \right)} \right) = OH’ = \frac{{R\sqrt 2 }}{2}\].
Tương tự, khoảng cách giữa mỗi đường thẳng AD, BC, BD và \[OO’\] đều bằng \[\frac{{R\sqrt 2 }}{2}\].
Từ đó suy ra các đuờng thẳng AC, AD, BC, BD đều tiếp xúc với mặt trụ có trục là \[OO’\] và có bán kính \[\frac{{R\sqrt 2 }}{2}\].
BÀI TẬP TỔNG HỢP
Bài tập 1. Cho mặt trụ tròn xoay T và một điểm S cố định không nằm trên T. Một đường thẳng d thay đồi luôn luôn đi qua S cắt T ở A và B. Chứng minh rằng trung điểm I của đoạn thẳng AB nằm trên một mặt trụ cố định.
HD-ĐS
Dùng mặt phẳng đi qua S và vuông góc với trục \[\Delta \] của mặt trụ tại K.
Bài tập 2. Một hình trụ có diện tích xung quanh là S diện tích đáy bằng diện tích một mặt cầu bán kính bằng a. Tính thể tích và diện tích thiết diện qua trục của hình trụ.
HD-ĐS
Kết quả \[V = Sa.S’ = \frac{S}{\pi }\]
Bài tập 3. Một hình trụ có thiết diện qua trục là hình vuông, diện tích xung quanh hình trụ là \[4\pi \]. Mặt phẳng \[\left( \alpha \right)\] song song với trục hình trụ và cắt nó theo thiết diện \[AB{B_1}{A_1}\]. Biết một cạnh của thiết diện là dây cung của đường tròn đáy căng một cung \[120^\circ \]. Tính diện tích toàn phần hình trụ và diện tích thiết diện \[AB{B_1}{A_1}\] và thể tích khối trụ.
HD-ĐS
Kết quả \[{S_{tp}} = 6\pi \], diện tích thiết diện \[2\sqrt 3 \]
Bài tập 4. Cho hình trụ có hai đáy \[\left( O \right),\left( {O’} \right)\], bán kính đáy bằng chiều cao a. Trên (O) lấy A, trên \[\left( {O’} \right)\] lấy B sao cho \[AB = 2a\]. Tính thể tích khối tứ diện \[OO’AB\].
HD-ĐS
Kết quả \[{V_{OO’AB}} = \frac{{{a^3}\sqrt 3 }}{{12}}\].
Bài tập 5. Cho một hình trụ có một chiều cao 2 và bán kính đáy 7. Gọi \[\left( O \right)\] và \[\left( {O’} \right)\] là hai đường tròn đáy. Một mặt phẳng (P) không song song với trục cắt đuờng tròn \[\left( O \right)\] tại A, B và cắt đuờng tròn \[\left( {O’} \right)\] tại C, D sao cho ABCD là hình vuông. Tính khoảng cách giữa trục \[OO’\] với đuờng thẳng CD.
HD-ĐS
Kết quả: \[d\left( {OO’;CD} \right) = 2\sqrt 6 \]
Bài tập 6. Cho hình trụ bán kính đáy R, chiều cao \[OO’ = h\], A và B là hai điểm thay đổi trên hai đường tròn đáy sao cho độ dài \[AB = a\] không đổi \[\left( {h < a < \sqrt {{h^2} + 4{R^2}} } \right)\]. Chứng minh góc và khoảng cách giữa hai đường thẳng AB và \[OO’\] không đổi.
HD-ĐS
Kết quả \[\sqrt {{R^2} – \frac{{{a^2} – {h^2}}}{4}} \] không đổi
Bài tập 7. Một khối trụ có bán kính đáy \[r = 5cm\], khoảng cách hai đáy bằng 7cm. Cắt khối trụ bởi một mặt phẳng song song với trục cách trục 3cm. Tính diện tích của thiết diện.
HD-ĐS
Kết quả \[S = 56c{m^2}\]
Bài tập 8. Cho hình hộp \[ABCD.{\rm{ }}{A_1}{B_1}{C_1}{D_1}\] nội tiếp trong một hình trụ cho trước, góc giữa đường thẳng \[{B_1}D\] và mặt phẳng \[\left( {AB{B_1}{A_1}} \right)\] bằng \[30^\circ \]. Khoảng cách từ trục hình trụ đến mặt \[AB{B_1}{A_1}\] bằng \[\frac{3}{2}a\]. Tính thể tích khối hộp và thể tích hình cầu ngoại tiếp hình hộp biết đường kính của đáy hình trụ bằng 5a.
HD-ĐS
Kết quả thể tích khối hộp: \[12{a^3}.\sqrt {11} \], khối cầu: \[36\pi {a^3}\].
Xem thêm