Câu hỏi:
Cho hình chóp \(S.{\mkern 1mu} ABCD\) có đáy \(ABCD\) là hình chữ nhật, \(AB = a,{\mkern 1mu} {\mkern 1mu} BC = 2a.\) Cạnh \(SA = 2a\) và vuông góc với mặt phẳng \(\left( {ABCD} \right).\) Khoảng cách giữa hai đường thẳng BD và SC bằng
A.\(\frac{{a\sqrt 2 }}{3}.\)
B.\(\frac{{a\sqrt 3 }}{2}.\)
C.\(\frac{{3a}}{2}.\)
D.\(\frac{{2a}}{3}.\)
Đáp án chính xác
Trả lời:
Chọn đáp án D
Dựng hình bình hành DBCPnhư hình vẽ.
Từ \(B{\rm{D // CP}} \Rightarrow {\rm{BD // }}\left( {SCP} \right) \Rightarrow d\left( {B{\rm{D}};SC} \right) = d\left( {D;(SCP)} \right) = \frac{1}{2}d\left( {A;(SCP)} \right)\).
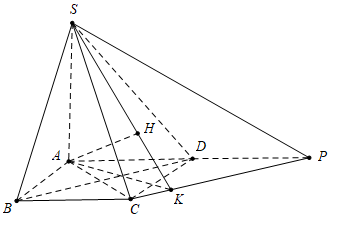Kẻ \(AK \bot CP,{\rm{ }}AH \bot SK \Rightarrow d\left( {A;\left( {SCP} \right)} \right) = AH\)
\( \Rightarrow d\left( {BD;SC} \right) = \frac{1}{2}AH.\)
Ta có \({S_{ACP}} = \frac{1}{2}AK.CP = \frac{1}{2}CD.AP = \frac{1}{2}a.4a = 2{a^2}.\)
Cạnh \(CP = BD = \sqrt {A{B^2} + A{D^2}} = a\sqrt 5 \Rightarrow AK = \frac{{4a}}{{\sqrt 5 }}.\)
\(\frac{1}{{A{H^2}}} = \frac{1}{{S{A^2}}} + \frac{1}{{A{K^2}}} = \frac{1}{{4{a^2}}} + \frac{5}{{16{a^2}}} \Rightarrow AH = \frac{{4a}}{3}\)
\( \Rightarrow d\left( {BD;SC} \right) = \frac{1}{2}AH = \frac{{2a}}{3}.\)
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Trong không gian Oxyz,cho đường thẳng \(d:\frac{{x – 2}}{2} = \frac{{y + 3}}{1} = \frac{{z – 1}}{{ – 2}}.\) Vectơ nào dưới đây là một vectơ chỉ phương của d?
Câu hỏi:
Trong không gian Oxyz,cho đường thẳng \(d:\frac{{x – 2}}{2} = \frac{{y + 3}}{1} = \frac{{z – 1}}{{ – 2}}.\) Vectơ nào dưới đây là một vectơ chỉ phương của d?
A.\(\vec u = \left( {2;3;1} \right).\)
B.\(\vec u = \left( {2;1; – 2} \right).\)
Đáp án chính xác
C.\(\vec u = \left( {2; – 3;1} \right).\)
D.\(\vec u = \left( {2;1;2} \right).\)
Trả lời:
Lời giải:
Chọn đáp án B
Đường thẳng \(d:\frac{{x – 2}}{2} = \frac{{y + 3}}{1} = \frac{{z – 1}}{{ – 2}}\) có một VTCP là \(\overrightarrow u = \left( {2;1; – 2} \right)\).====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho hàm số f(x) có bảng biến thiên như sau:
Giá trị cực tiểu của hàm số đã cho là
Câu hỏi:
Cho hàm số f(x) có bảng biến thiên như sau:
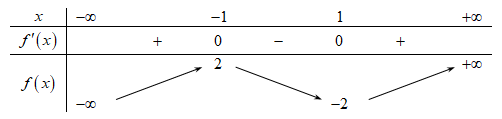
Giá trị cực tiểu của hàm số đã cho làA.2.
B.−1.
C.−2.
Đáp án chính xác
D.1.
Trả lời:
Chọn đáp án C
Giá trị cực tiểu của hàm số \(f\left( x \right)\) là \( – 2\).====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho hàm số f(x) có bảng biến thiên như sau:Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
Câu hỏi:
Cho hàm số f(x) có bảng biến thiên như sau:
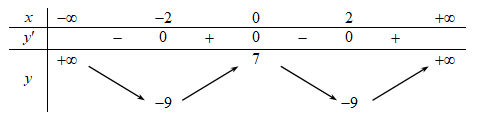Hàm số đã cho nghịch biến trên khoảng nào dưới đây?A.\(\left( { – 2;0} \right).\)
B.\(\left( { – \infty ; – 2} \right).\)
Đáp án chính xác
C.\(\left( {2; + \infty } \right).\)
D.\(\left( { – 2; + \infty } \right).\)
Trả lời:
Chọn đáp án BHàm số \(f\left( x \right)\) nghịch biến trên \(\left( { – \infty ; – 2} \right)\).
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Trong không gian Oxyz,cho mặt phẳng \(\left( P \right):x – 6y + 12 = 0.\) Vectơ nào dưới đây là một vectơ pháp tuyến của (P)?
Câu hỏi:
Trong không gian Oxyz,cho mặt phẳng \(\left( P \right):x – 6y + 12 = 0.\) Vectơ nào dưới đây là một vectơ pháp tuyến của (P)?
A.\(\vec n = \left( {1; – 6;0} \right).\)
Đáp án chính xác
B.\(\vec n = \left( {1; – 6;12} \right).\)
C.\(\vec n = \left( {1;0; – 6} \right).\)
D.\(\vec n = \left( {1;6;0} \right).\)
Trả lời:
Chọn đáp án A
Mặt phẳng \(\left( P \right):x – 6y + 12 = 0\) có một VTPT là \(\overrightarrow n = \left( {1; – 6;0} \right)\).====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình vẽ ?
Câu hỏi:
Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình vẽ ?
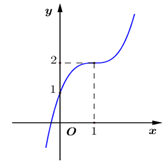
A.\(y = {x^3} – 3{x^2} + 3x + 1.\)
Đáp án chính xác
B.\(y = – {x^3} + 3{x^2} + 1.\)
C.\(y = {x^3} – 3x + 4.\)
D.\(y = – {x^3} – 3{x^2} – 1.\)
Trả lời:
Chọn đáp án A
Ta có \(y\left( 1 \right) = 2 \Rightarrow \) Loại B và D. Mà \(y\left( 0 \right) = 1 \Rightarrow \) Chọn A.====== **** mời các bạn xem câu tiếp bên dưới **** =====