Cho hàm số  \(y = f\left( x \right)\). Hàm số \(y = f'\left( x \right)\) có bảng biến thiên như sau: Bất phương trình \(f\left( x \right) > {2^x} + m\) đúng với mọi \(x \in \left( { – 1;1} \right)\) khi và chỉ khi

Câu hỏi:

Cho hàm số  \(y = f\left( x \right)\). Hàm số \(y = f’\left( x \right)\) có bảng biến thiên như sau:

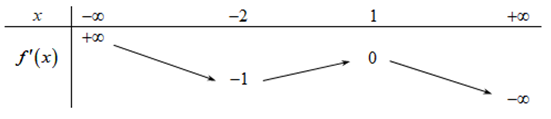
Bất phương trình \(f\left( x \right) > {2^x} + m\) đúng với mọi \(x \in \left( { – 1;1} \right)\) khi và chỉ khi

A. \(m < f\left( 1 \right) – 2\)                       

B. \(m \le f\left( 1 \right) – 2\)         

Đáp án chính xác

C. \(m \le f\left( { – 1} \right) – \frac{1}{2}\)                 

D. \(m < f\left( { – 1} \right) – \frac{1}{2}\)

Trả lời:

Đáp án B
Xét hàm số \(g\left( x \right) = f\left( x \right) – {2^x},x \in \left( { – 1;1} \right) \Rightarrow g’\left( x \right) = f’\left( x \right) – {2^x}\ln 2\)
Với mọi \(x \in \left( { – 1;1} \right)\) thì \(f’\left( x \right) < 0 \Rightarrow g’\left( x \right) < 0,\forall x \in \left( { – 1;1} \right)\)
\( \Rightarrow g\left( x \right)\) nghịch biến trên \(\left( { – 1;1} \right)\)
Khi đó \(m < g\left( x \right),\forall x \in \left( { – 1;1} \right) \Leftrightarrow m \le g\left( 1 \right) \Leftrightarrow m \le f\left( 1 \right) – 2\). Chọn B.

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Với a là số thực dương tùy ý, \({\log _2}\left( {8a} \right)\) bằng
   
   

   Câu hỏi:
   

   Với a là số thực dương tùy ý, \({\log _2}\left( {8a} \right)\) bằng

   A. \(3 + {\log _2}a\)   

   Đáp án chính xác

   B. \(4 + {\log _2}a\)   

   C. \(8{\log _2}a\)       

   D. \(3{\log _2}a\)

   Trả lời:

   Đáp án A
   Ta có \({\log _2}\left( {8a} \right) = {\log _2}8 + {\log _2}a = 3 + {\log _2}a\). Chọn A.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Trong không gian Oxyz, cho mặt phẳng P:3x−4y+5z−2=0. Vectơ nào dưới đây là một vectơ pháp tuyến của (P)?
   
   

   Câu hỏi:
   

   Trong không gian Oxyz, cho mặt phẳng $\left(P\right):3x-4y+5z-2=0$. Vectơ nào dưới đây là một vectơ pháp tuyến của (P)?

   A. $\overrightarrow{n}=\left(-4;5;-2\right)$

   B. $\overrightarrow{n}=\left(3;-4;2\right)$

   C. $\overrightarrow{n}=\left(3;-5;-2\right)$

   D. $\overrightarrow{n}=\left(3;-4;5\right)$

   Đáp án chính xác

   Trả lời:

   Đáp án D
   Mặt phẳng $\left(P\right):3x-4y+5z-2=0$ có một VTPT là $\overrightarrow{n}=\left(3;-4;5\right)$. Chọn D.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Số phức \(z = 2 – 3i\) có phần ảo bằng
   
   

   Câu hỏi:
   

   Số phức \(z = 2 – 3i\) có phần ảo bằng

   A. 2.                          

   B. \( – 3\)                    

   Đáp án chính xác

   C. \( – 2\)                   

   D. \( – 3i\)

   Trả lời:

   Đáp án B
   Số phức \(z = 2 – 3i\) có phần ảo bằng \( – 3\). Chọn B.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Cho cấp số cộng \(\left( {{u_n}} \right)\) với \({u_2} = 6,{u_5} = 21\). Tính d.
   
   

   Câu hỏi:
   

   Cho cấp số cộng \(\left( {{u_n}} \right)\) với \({u_2} = 6,{u_5} = 21\). Tính d.

   A. \(d = 3\)                

   B. \(d = 2\)                 

   C. \(d = 4\)                

   D. \(d = 5\)

   Đáp án chính xác

   Trả lời:

   Đáp án D
   Ta có \(\left\{ \begin{array}{l}{u_2} = 6\\{u_5} = 21\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{u_1} + d = 6\\{u_1} + 4d = 21\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{u_1} = 1\\d = 5\end{array} \right. \Rightarrow \)Chọn D

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Cho hàm số \(f\left( x \right)\) có bảng biến thiên như sau: Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
   
   

   Câu hỏi:
   

   Cho hàm số \(f\left( x \right)\) có bảng biến thiên như sau:
   
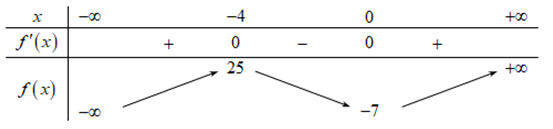
   Hàm số đã cho nghịch biến trên khoảng nào dưới đây?

   A. \(\left( { – 7;25} \right)\)                         

   B. \(\left( { – \infty ; – 4} \right)\)    

   C. \(\left( { – 4;0} \right)\)              

   Đáp án chính xác

   D. \(\left( {0; + \infty } \right)\)

   Trả lời:

   Đáp án C
   Hàm số \(f\left( x \right)\) nghịch biến trên \(\left( { – 4;0} \right)\). Chọn C.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====