Trong không gian Oxyz, cho mặt phẳng \(\left( P \right):x – 2y + 3z – 1 = 0\) và hai điểm \(A\left( {2; – 1;1} \right),B\left( { – 2;1;1} \right)\). Kí hiệu \({d_1}\) và \({d_2}\) lần lượt là khoảng cách từ điểm A và B đến mặt phẳng \(\left( P \right)\). Tính tỉ số \(\frac{{{d_1}}}{{{d_2}}}\).

Câu hỏi:

Trong không gian Oxyz, cho mặt phẳng \(\left( P \right):x – 2y + 3z – 1 = 0\) và hai điểm \(A\left( {2; – 1;1} \right),B\left( { – 2;1;1} \right)\). Kí hiệu \({d_1}\) và \({d_2}\) lần lượt là khoảng cách từ điểm A và B đến mặt phẳng \(\left( P \right)\). Tính tỉ số \(\frac{{{d_1}}}{{{d_2}}}\).

A. \(\frac{{{d_1}}}{{{d_2}}} = 3.\)             

Đáp án chính xác

B. \(\frac{{{d_1}}}{{{d_2}}} = 2.\)   

C. \(\frac{{{d_1}}}{{{d_2}}} = \frac{1}{3}.\)      

D. \(\frac{{{d_1}}}{{{d_2}}} = \frac{1}{2}.\)

Trả lời:

Đáp án A
Ta có \({d_1} = \frac{{\left| {2 – 2.\left( { – 1} \right) + 3.1 – 3} \right|}}{{\sqrt {{1^2} + {{\left( { – 2} \right)}^2} + {3^2}} }} = \frac{6}{{\sqrt {14} }}\) và \({d_1} = \frac{{\left| { – 2 – 2.1 + 3.1 – 1} \right|}}{{\sqrt {{1^2} + {{\left( { – 2} \right)}^2} + {3^2}} }} = \frac{2}{{\sqrt {14} }}\).
\(\frac{{{d_1}}}{{{d_2}}} = \frac{6}{{\sqrt {14} }}:\frac{2}{{\sqrt {14} }} = 3\).

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Trong không gian Oxyz, cho mặt phẳng \(\left( P \right):x – 2y + z + 3 = 0\). Mặt phẳng \(\left( P \right)\) đi qua điểm có tọa độ nào dưới đây?
   
   

   Câu hỏi:
   

   Trong không gian Oxyz, cho mặt phẳng \(\left( P \right):x – 2y + z + 3 = 0\). Mặt phẳng \(\left( P \right)\) đi qua điểm có tọa độ nào dưới đây?

   A. \(\left( { – 1;2;0} \right).\)                       

   B. \(\left( {1; – 2;0} \right).\)  

   C. \(\left( { – 1; – 2;0} \right).\)              

   D. \(\left( {1;2;0} \right).\)

   Đáp án chính xác

   Trả lời:

   Đáp án D
   Mặt phẳng \(\left( P \right)\) đi qua điểm có tọa độ \(\left( {1;2;0} \right)\) vì \(1 – 2.2 + 0 + 3 = 0\).

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Số phức \(z = 6 + 8i\) có môđun bằng:
   
   

   Câu hỏi:
   

   Số phức \(z = 6 + 8i\) có môđun bằng:

   A. 5.                          

   B. 14.                        

   C. 10.                        

   Đáp án chính xác

   D. \(\sqrt {14} .\)

   Trả lời:

   Đáp án C
   Số phức \(z = 6 + 8i\) có môđun bằng $\sqrt{6^2+8^2}=10$

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Cho hàm số  có bảng biến thiên như sau: Hàm số đã cho đạt cực tiểu tại:
   
   

   Câu hỏi:
   

   Cho hàm số  có bảng biến thiên như sau:
   
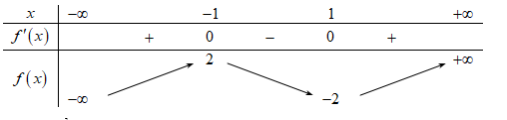
   Hàm số đã cho đạt cực tiểu tại:

   A.  x = 1                           

   Đáp án chính xác

   B. x = -2                          

   C.  x = -1                        

   D. x = 2

   Trả lời:

   Đáp án A
   Hàm số \(f\left( x \right)\) đạt cực tiểu tại \(x = 1\).

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Với a là số thực dương tùy ý, log28a  bằng
   
   

   Câu hỏi:
   

   Với a là số thực dương tùy ý, ${\log }_2\frac{8}{a}$  bằng

   A. \( – 8{\log _2}a.\)     

   B. \(3 – {\log _2}a.\)   

   Đáp án chính xác

   C. \(\frac{8}{{{{\log }_2}a}}.\)        

   D. \(3 + {\log _2}a.\)

   Trả lời:

   Đáp án B
   Ta có \({\log _2}\frac{8}{a} = {\log _2}8 – {\log _2}a = 3 – {\log _2}a\).

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Cho ∫01fxdx=3. Tính I=∫012fxdx.
   
   

   Câu hỏi:
   

   Cho $\underset{0}{\overset{1}{\int }}f\left(x\right)dx=3$. Tính $I=\underset{0}{\overset{1}{\int }}2f\left(x\right)dx$.

   A. \(I = 3.\)                

   B. \(I = \frac{2}{3}.\)

   C. \(I = 6.\)                

   Đáp án chính xác

   D. \(I = \frac{3}{2}.\)

   Trả lời:

   Đáp án C
   Ta có $I=\underset{0}{\overset{1}{\int }}2f\left(x\right)dx=2\underset{0}{\overset{1}{\int }}f\left(x\right)dx=6$.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====