Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây
Các dạng bài tập vận dụng cao ứng dụng của tích phân
Bài 3. Ứng dụng hình học tích phân
A. Kiến thức sách giáo khoa cần nắm
I. Diện tích hình phẳng
1. Định lý 1:
Cho hàm số y = f(x) liên tục, không âm trên [a ; b]. Khi đó diện tích S của hình thang cong giới hạn bởi đồ thị hàm số y = f(x), trục hoành và 2 đường thẳng x = a. x = b là: \(S = \int_a^b f (x)dx\)
2. Bài toán liên quan
Bài toán 1: Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f(x) liên tục trên đoạn [a ; b], trục hoành và hai đường thẳng x = a, x = b được xác định: \(S = \int_a^b | f(x)|dx\)
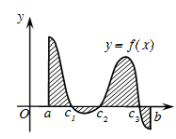
Bài toán 2: Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f(x), y = g(x) liên tục trên đoạn [a ; b] và hai đường thẳng x = a, x = b được xác định: \(S = \int_a^b | f(x) – g(x)|dx\)
Chú ý: Nếu trên đoạn [a ; b], hàm số f(x) không đổi dấu thì: \(\int_a^b | f(x)|dx = \left| {\int_a^b f (x)dx} \right|\)
Bài toán 3: Diện tích của hình phẳng giới hạn bởi các đường x = g(y), x = h(y) và hai đường thẳng y = x; y = d được xác định: \(S = \int_c^d | g(y) – h(y)|dy\)
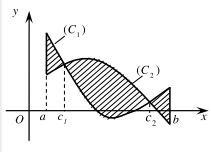
Bài toán 4: Diện tích hình phẳng giới hạn bởi 2 đồ thị \(\left( {{C_1}} \right):{f_1}(x),\left( {{C_2}} \right):{f_2}(x)\) là: \(S = \int_{{x_1}}^{{x_2}} | f(x) – g(x)|dx\). Trong đó: \({x_1},{x_2}\) tương ứng là nghiệm của phương trình \(f(x) = g(x),\left( {{x_1} < {x_2}} \right)\)
II. Thể tích của khối tròn xoay
1. Thể tích vật thể
Gọi B là phần vật thể giới hạn bởi hai mặt phẳng vuông góc với trục Ox tại các điểm a và b; S(x) là diện tích thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm x, \((a \le x \le b)\). Giả sử S(x) là hàm số liên tục trên đoạn [a ; b].
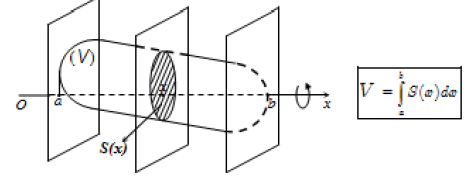
2. Thể tích khối tròn xoay
Bài toán 1: Thể tích khối tròn xoay được sinh ra khi quay hình phẳng giới hạn bởi các đường y = f(x), trục hoành và hai đường thẳng x = a, x = b quanh trục Ox :
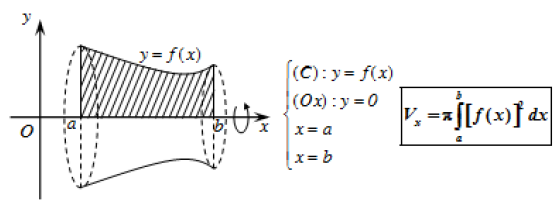
Bài toán 2: Thể tích khối tròn xoay được sinh ra khi quay hình phẳng giới hạn bởi các đường \(x = g(y)\), trục hoành và hai đường thẳng y = c, y = d quanh trục Oy :
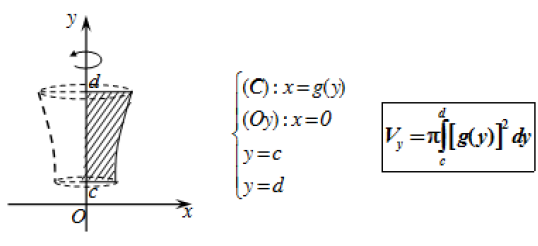
Bài toán 3: Thể tích khối tròn xoay được sinh ra khi quay hình phẳng giới hạn bởi các đường y = f(x), y = g(x) và hai đường thẳng x = a; x = b quanh trục Ox\(V = \pi \int_a^b {\left| {{f^2}(x) – {g^2}(x)} \right|} dx\).
B. Phân loại và phương pháp giải bài tập
Dạng 1: Tính diện tích giới hạn bởi 1 đồ thị
1. Phương pháp:
a. Phương pháp 1:
\(S = \int_a^b | f(x)|dx\)
* Xét dấu biểu thức \(f(x);x \in [a;b]\), phá dấu trị tuyệt đối và tính tích phân.
b. Phương pháp 2:
* Giải phương trình f(x) = 0; chọn nghiệm trong [a ; b]. Giả sử các nghiệm là \(\alpha ;\beta \) với \(\alpha < \beta \).
* Áp dụng tính chất liên tục của hàm số f(x) trên [a ; b]; ta có:
\(S = \left. {} \right|_a^\alpha f(x){\rm{d}}x| + |_\alpha ^\beta f(x){\rm{d}}x| + |_\beta ^bf(x){\rm{d}}x\mid \)
2. Các Bài tập mẫu:
Bài tập 1: Tính diện tích S của hình phẳng giới hạn bởi đồ thị \({\rm{y}} = {{\rm{x}}^2}\), trục hoành và đường thẳng x = 2.
A. \(S = \frac{8}{9}\)
B. \(S = \frac{{16}}{3}\).
C. \(S = 16\).
D. \(S = \frac{8}{3}\).
Hướng dẫn giải
CHỌN D
Nhận thấy rằng, để tính diện tích ta cần phải tìm được 2 cận. Để tìm thêm cận còn lại ta giải phương trình hoành độ giao điểm của đồ thị \(({\rm{P}}):{\rm{y}} = {{\rm{x}}^2}\) với trục hoành.
Phương trình hoành độ giao điểm của đồ thị \(({\rm{P}}):{\rm{y}} = {{\rm{x}}^2}\) với trục hoành: \({{\rm{x}}^2} = 0 \Leftrightarrow {\rm{x}} = 0\)
Áp dụng công thức ta có \(S = \int_0^2 {\left| {{x^2}} \right|} dx = \frac{8}{3}\).
Nhận xét: Nếu ta vẽ đồ thị hàm số \({\rm{y}} = {{\rm{x}}^2}\) và đường thẳng x = 2 ta dễ dàng xác định được hình phẳng giới hạn bởi các đường này. Từ đó ta dễ dàng tính được diện tích S.
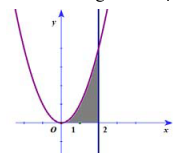
Bài tập 2: Tính diện tích hình phẳng giới hạn bởi đồ thị các hàm số \({\rm{y}} = {{\rm{x}}^2}\). \({{\rm{e}}^{\rm{x}}}\), trục hoành và đường thẳng x = 1
A. e – 2.
B. 2 + e.
C. 2 – e.
D. 1 .
Hướng dẫn giải
CHỌN A
Phương trình hoành độ giao điểm \({{\rm{x}}^2}{{\rm{e}}^{\rm{x}}} = 0 \Leftrightarrow {\rm{x}} = 0\)
Ta có:
\(\begin{array}{l}S = \int_0^1 {{x^2}} {e^x}dx = \int_0^1 {{x^2}} d\left( {{e^x}} \right) = \left. {{x^2}{e^x}} \right|_0^1 – \int_0^1 {{e^x}} d\left( {{x^2}} \right)\\ = e – 2\int_0^1 x {e^x}dx = e – 2\int_0^1 x d\left( {{e^x}} \right) = e – \left. {2x{e^x}} \right|_0^1 + 2\int_0^1 {{e^x}} dx\end{array}\)
\( = {\rm{e}} – 2{\rm{e}} + \left. {2{{\rm{e}}^{\rm{x}}}} \right|_0^1 = – {\rm{e}} + 2{\rm{e}} – 2 = {\rm{e}} – 2.\)
Lời bình: Bài toán trên đã có 1 cận, ta chỉ cần tìm thêm 1 cận nữa bằng cách giải phương trình hoành độ giao điểm. Sau đó áp dụng công thức. Nếu vẽ đồ thị bài này để tìm hình phẳng giới hạn bởi các đường là không nên vì đồ thị hàm số hơi phức tạp. Việc tìm được công thức \(S = \int_0^1 {{x^2}} {e^x}dx\) và tính tích phân này ta có thể dùng MTCT để tính và chọn Chọn.
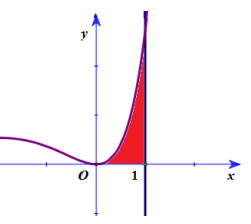
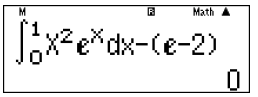
Bài tập 3: Tính diện tích hình phẳng giới hạn bởi đồ thị \({\rm{y}} = \sqrt {1 – {{\rm{x}}^2}} \) và trục hoành:
A. \(\pi – 2\).
B. \(\frac{\pi }{4}\).
C. 1 .
D. \(\frac{\pi }{2}\).
Hướng dẫn giải
CHỌN D
Phương trình hoành độ giao điểm của, Ox là \(\sqrt {1 – {{\rm{x}}^2}} = 0 \Leftrightarrow {\rm{x}} = \pm 1\)
Khi đó, diện tích hình phẳng cần tìm là \(S = \int_{ – 1}^1 {\sqrt {1 – {x^2}} } dx\).
Đặt \(x = \sin t \Leftrightarrow dx = \cos tdt\) và \(\left\{ {\begin{array}{*{20}{c}}{x = 1 \to t = \frac{\pi }{2}}\\{x = – 1 \to t = – \frac{\pi }{2}}\end{array}} \right.\)
Suy ra \(S = \int_{ – 1}^1 {\sqrt {1 – {x^2}} } dx = \int_{ – \frac{\pi }{2}}^{\frac{\pi }{2}} {\sqrt {1 – {{\sin }^2}t} } t\cos tdt = \int_{ – \frac{\pi }{2}}^{\frac{\pi }{2}} {{{\cos }^2}} tdt = \frac{\pi }{2}\)
Lời bình: Bài toán trên chưa có cận, ta phải giải phương trình hoành độ giao điểm để tìm cận. Sau đó áp dụng công thức. Việc tìm được công thức \({\rm{S}} = \int_{ – 1}^1 {\sqrt {1 – {{\rm{x}}^2}} } {\rm{dx}}\) và tính tích phân này tương đối phức tạp, do đó ta có thể dùng MTCT để tính và chọn Chọn.
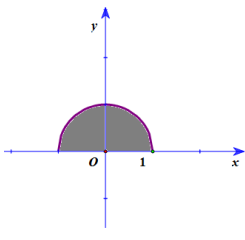
Nếu vẽ được đồ thị thì ta xác định được hình phẳng và diện tích của nó dễ dàng, đó chính là diện tích của nữa đường tròn bán kính bằng 1 . Do đó: \({\rm{S}} = \frac{1}{2}\pi {{\rm{R}}^2} = \frac{\pi }{2}\).
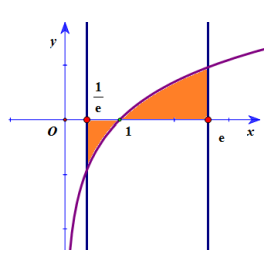
Bài tập 4: Tính diện tích S hình phẳng giới hạn bởi các đường \({\rm{y}} = \ln {\rm{x}},{\rm{x}} = {\rm{e}},{\rm{x}} = \frac{1}{{\rm{e}}}\) và trục hoành
A. \(S = 2 – \frac{2}{{\rm{e}}}\).
B. \({\rm{S}} = 1 – \frac{1}{{\rm{e}}}\).
C. \({\rm{S}} = 2 + \frac{2}{{\rm{e}}}\).
D. \({\rm{S}} = 1 + \frac{1}{{\rm{e}}}\).
Hướng dẫn giải
CHỌN A
Phương trình hoành độ giao điểm của đồ thị y = lnx và trụ hoành là lnx = 0 \( \Leftrightarrow \)x = 1.
\(\begin{array}{l}S = \int_{\frac{1}{c}}^e | \ln x|dx = – \int_{\frac{1}{c}}^1 {\ln } xdx + \int_1^e {\ln } x \cdot dx\\ = \left. {(x – x\ln x)} \right|_{\frac{1}{c}}^1 + \left. {(x\ln x – x)} \right|_1^e = 2 – \frac{2}{e}\end{array}\)
Bài tập 5: Diện tích tam giác được cắt ra bởi các trục tọa độ và tiếp tuyến của đồ thị y = lnx tại giao điểm của đồ thị hàm số với trục Ox là:
A. \({\rm{S}} = \frac{2}{3}\)
B. \({\rm{S}} = \frac{1}{4}\)
C. \({\rm{S}} = \frac{2}{5}\)
D. \({\rm{S}} = \frac{1}{2}\)
Hướng dẫn giải
Chọn D
Phương trình hoành độ giao điểm: \(\ln x = 0 \Leftrightarrow x = 1\)
Ta có: \({{\rm{y}}^\prime } = {(\ln {\rm{x}})^\prime } = \frac{1}{{\rm{x}}} \cdot {{\rm{y}}^\prime }(1) = 1\)
Phương trình tiếp tuyến của đồ thị y = lnx tại giao điểm của đồ thị hàm số với trục Ox là:
y = 1(x – 1) + 0 hay y = x – 1
Đường thẳng y = x – 1 cắt Ox tại điểm A(1;0) và cắt Oy tại điểm B(0; -1).
Tam giác vuông OAB có
\(\begin{array}{l}{S_D} = \int_a^b | f(x)|dx = \int_a^0 | f(x)|dx + \int_0^b | f(x)|dx\\ = – \int_a^0 f (x)dx + \int_0^b f (x)dx\end{array}\)
Bài tập 6: Diện tích hình phẳng giới hạn bởi đường cong \({\rm{y}} = 2\sqrt {{\rm{ax}}} ({\rm{a}} > 0)\), trục hoành và đường thẳng x = a bằng \({\rm{k}}{{\rm{a}}^2}\). Tính giá trị của tham số k.
A. \({\rm{k}} = \frac{7}{3}\)
B. \({\rm{k}} = \frac{4}{3}\)
C. \({\rm{k}} = \frac{{12}}{5}\)
D. \({\rm{k}} = \frac{6}{5}\)
Hướng dẫn giải
Chọn B
Có \({\rm{S}} = \int_0^{\rm{a}} | 2\sqrt {{\rm{ax}}} |{\rm{dx}} = \left. {2\sqrt {\rm{a}} \cdot \frac{2}{3} \cdot {{\rm{x}}^{\frac{3}{2}}}} \right|_0^{\rm{a}} = \frac{4}{3}{{\rm{a}}^2} = {\rm{k}}{{\rm{a}}^2} \Rightarrow {\rm{k}} = \frac{4}{3}\)
Xem thêm