Bài toán về góc – Góc giữa hai đường thẳng có đáp án

Tài liệu Bài toán về góc – Góc giữa hai đường thẳng có đáp án gồm các nội dung chính sau:

A. Phương phương giải

– Gồm phương pháp giải Bài toán về góc – Góc giữa hai đường thẳng.

B. Bài tập minh họa

– Gồm 8 bài tập có đáp án và lời giải chi tiết giúp học sinh tự rèn luyện cách giải các dạng Bài toán về góc – Góc giữa hai đường thẳng.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây:

BÀI TOÁN VỀ GÓC – GÓC GIỮA HAI ĐƯỜNG THẲNG

A. PHƯƠNG PHÁP GIẢI

Định nghĩa góc giữa hai đường thẳng

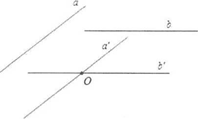
Trong không gian cho 2 đường thẳng a, b bất kỳ.

Từ một điểm O nào đó ta vẽ 2 đường thẳng $a^{‘}$, $b^{‘}$ lần lượt song song với a và b. Ta nhận thấy rằng khi điểm O thay đổi thì góc giữa 2 đường thẳng $a^{‘}$ và $b^{‘}$  không thay đổi.

Do đó ta có định nghĩa:

Định nghĩa: Góc giữa 2 đường thẳng a và b trong không gian là góc giữa 2 đường thẳng $a^{‘}$ và $b^{‘}$ cùng đi qua một điểm và lần lượt song song với a và b.

2. Cách xác định góc giữa hai đường thẳng

Để xác định góc giữa 2 đường thẳng a và b ta có thể lấy điểm O thuộc một trong hai đường thẳng đó rồi vẽ một đường thẳng qua O và song song với đường thẳng còn lại.

Nếu $\overrightarrow{u}$ là vecto chỉ phương của đường thẳng a và $\overrightarrow{v}$ là vecto chỉ phương của đường thẳng b và $\left(\overrightarrow{u};\overrightarrow{v}\right)=\alpha$ thì góc giữa 2 đường thẳng a và b bằng $\alpha$ nếu $0\le \alpha \le 90°$ và bằng $90°<\alpha \le 180°$ nếu . Nếu 2 đường thẳng a và b song song hoặc trùng nhau thì góc giữa chúng bằng $0°$. Góc giữa 2 đường thẳng là góc có số đo $0\le \alpha \le 90°$.

3. Phương pháp tính góc giữa hai đường thẳng

Để tính góc giữa hai đường thẳng trong không gian chúng ta cần nhớ các công thức sau: 

■ Định lý hàm số cosin trong tam giác ABC: $\cos \widehat{BAC}=\frac{A{B}^2+A{C}^2-B{C}^2}{2.AB.AC}$

Tương tự ta có:

$\cos \widehat{ABC}=\frac{B{A}^2+B{C}^2-A{C}^2}{2.BA.BC}$ và $\cos \widehat{ACB}=\frac{C{A}^2+C{B}^2-A{B}^2}{2.CA.CB}$

Chú ý: $\overrightarrow{AB}.\overrightarrow{AC}=AB.AC\cos \widehat{BAC}=\frac{1}{2}\left(A{B}^2+A{C}^2-B{C}^2\right)$

■ Tính góc giữa hai đường thẳng AB và CD ta tính góc giữa hai vectơ $\overrightarrow{AB}$ và $\overrightarrow{CD}$ dựa vào công thức

$\cos \left(\overrightarrow{AB};\overrightarrow{CD}\right)=\frac{\overrightarrow{AB}.\overrightarrow{CD}}{\left|\overrightarrow{AB}\right|.\left|\overrightarrow{CD}\right|}\Rightarrow \cos \left(AB;CD\right)=\frac{\left|\overrightarrow{AB}.\overrightarrow{CD}\right|}{\left|\overrightarrow{AB}\right|.\left|\overrightarrow{CD}\right|}$ từ đó suy ra góc giữa hai đường thẳng AB và CD.

B. BÀI TẬP MINH HỌA

Ví dụ 1: Cho hình chóp S.ABC có đáy là tam giác đều cạnh a, $SA\perp \left(ABC\right)$ và $SA=a\sqrt{3}$. Gọi M, N lần lượt là trung điểm của AB và SC. Tính cosin góc giữa hai đường thẳng AN và CM.

Lời giải

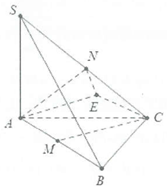
Cách 1: Dựng hình bình hành AMCE suy ra $AM=CE=\frac{a}{2}$.

Khi đó $AE//CM\Rightarrow \left(\widehat{AE;CM}\right)=\left(\widehat{AN;AE}\right)=\phi .$

Mặt khác $SC=\sqrt{S{A}^2+A{C}^2}=2a\Rightarrow$ độ dài đường trung tuyến AN là $AN=\frac{SC}{2}=a.AE=CM=\frac{a\sqrt{3}}{2}.$

Do $\Delta ABC$ đều nên $CM\perp AM\Rightarrow$ AMCE là hình chữ nhật.

Khi đó $CE\perp AE$ mà $CE\perp SA\Rightarrow CE\perp \left(SAE\right)\Rightarrow CE\perp SE.$

$\Delta SEC$ vuông tại E có đường trung tuyến $EN=\frac{1}{2}SC=a.$

Ta có: $\cos \widehat{NAE}=\frac{A{N}^2+A{E}^2-N{E}^2}{2.AN.AE}=\frac{\sqrt{3}}{4}>0\Rightarrow \cos \phi =\frac{\sqrt{3}}{4}.$

Cách 2: Ta có:

 $\overrightarrow{AN}=\frac{1}{2}\left(\overrightarrow{AS}+\overrightarrow{AC}\right);\overrightarrow{CM}=\overrightarrow{AM}-\overrightarrow{AC}=\frac{1}{2}\overrightarrow{AB}-\overrightarrow{AC}.$

Khi đó

 $\overrightarrow{AN}.\overrightarrow{CM}=\frac{1}{2}\left(\overrightarrow{AS}+\overrightarrow{AC}\right)\left(\frac{1}{2}\overrightarrow{AB}-\overrightarrow{AC}\right)=\frac{1}{4}\overrightarrow{AB}.\overrightarrow{AC}-\frac{1}{2}A{C}^2=\frac{1}{4}{a}^2\cos 60°-\frac{a^2}{2}=\frac{-3a^2}{8}.$

Lại có:

$AN=\frac{SC}{2}=a;CM=\frac{a\sqrt{3}}{2}\Rightarrow \cos \phi =\frac{\left|\frac{-3a^2}{8}\right|}{a.\frac{a\sqrt{3}}{2}}=\frac{\sqrt{3}}{4}.$

Bình luận: Dựa vào hai cách làm trên ta thấy rằng, trong một số trường hợp, việc sử dụng công cụ vectơ để tính góc giữa hai đường thẳng giúp bài toán trở nên dễ ràng hơn rất nhiều!.

Ví dụ 2: Cho hình chóp S.ABC có $SA=SB=SC=AB=a;AC=a\sqrt{2}$ và $BC=a\sqrt{3}$. Tính cosin góc giữa hai đường thẳng SC và AB.

 

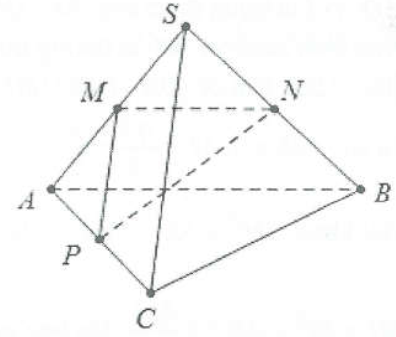
Lời giải

Cách 1: Gọi M, N, P lần lượt là trung điểm của SA, SB và AC. Khi đó \[\left\{ \begin{array}{l}MP//SC\\N//AB\end{array} \right. \Rightarrow \left( {\widehat {SC;AB}} \right) = \left( {\widehat {MP;MN}} \right).\]

Ta có: \[MN = \frac{{AB}}{2} = \frac{a}{2};MP = \frac{{SC}}{2} = \frac{a}{2}.\]

Mặt khác

\[\Delta SAC\] vuông tại S \[ \Rightarrow SP = \frac{{AC}}{2} = \frac{{a\sqrt 2 }}{2}.\]

\[B{P^2} = \frac{{B{A^2} + B{C^2}}}{2} – \frac{{A{C^2}}}{4} = \frac{3}{2}{a^2} \Rightarrow BP = \frac{{a\sqrt 6 }}{2}.\]

Suy ra

\[P{N^2} = \frac{{P{S^2} + P{B^2}}}{2} – \frac{{S{B^2}}}{4} = \frac{{3{a^2}}}{4} \Rightarrow NP = \frac{{a\sqrt 3 }}{2}.\]

Khi đó

\[\cos \widehat {NMP} = \frac{{M{N^2} + M{P^2} – N{P^2}}}{{2.MN.MP}} =  – \frac{1}{2} \Rightarrow \widehat {NMP} = 120^\circ  \Rightarrow \varphi  = \left( {\widehat {SC;AB}} \right) = 60^\circ .\]

Cách 2: Ta có:

\[\overrightarrow {AB}  = \overrightarrow {SB}  – \overrightarrow {SA}  \Rightarrow \overrightarrow {AB} .\overrightarrow {SC}  = \left( {\overrightarrow {SB}  – \overrightarrow {SA} } \right).\overrightarrow {SC}  = \overrightarrow {SB} .\overrightarrow {SC}  – \overrightarrow {SA} .\overrightarrow {SC} \]

\[ = \frac{1}{2}\left( {S{B^2} + S{C^2} – A{C^2}} \right) – \frac{1}{2}\left( {S{A^2} + S{C^2} – A{B^2}} \right) =  – \frac{{{a^2}}}{2}.\]

Suy ra

\[\cos \left( {SC;AB} \right) = \frac{{\left| {\frac{{ – {a^2}}}{2}} \right|}}{{a.a}} = \frac{1}{2} \Rightarrow \left( {SC;AB} \right) = 60^\circ .\]

Ví dụ 3: Cho tứ diện ABCD có \[AB = {x_1},CD = {x_2};AC = {y_1},BD = {y_2},BC = {z_1},AD = {z_2}\]. Tính góc giữa hai đường thẳng BC và AD.

Lời giải

Ta có:

\[\overrightarrow {BC} .\overrightarrow {DA} {\rm{ }} = {\rm{ }}\overrightarrow {BC} \left( {\overrightarrow {DC}  + \overrightarrow {CD} } \right) = \overrightarrow {CB} .\overrightarrow {CD}  – \overrightarrow {CB} .\overrightarrow {CD} \]

\[ = \frac{1}{2}\left( {C{B^2} + C{D^2} – B{D^2}} \right) – \frac{1}{2}\left( {C{B^2} + C{A^2} – A{B^2}} \right) = \frac{1}{2}\left( {A{B^2} + C{D^2} – B{D^2} – C{A^2}} \right).\]

Khi đó

\[\cos \left( {BC;DA} \right) = \frac{{\left| {\overrightarrow {BC} .\overrightarrow {DA} } \right|}}{{BC.DA}} = \frac{{x_1^2 + x_2^2 + y_1^2 – y_2^2}}{{2{z_1}{z_2}}}.\]

Đặc biệt: Nếu \[AB = CD = x;AC = BD = y\] và \[BC = AD = z\] ta đặt \[\left\{ \begin{array}{l}\alpha  = \left( {\widehat {BC;AD}} \right)\\\beta  = \left( {\widehat {AB;CD}} \right)\\\gamma  = \left( {\widehat {AC;BD}} \right)\end{array} \right.\] thì ta có:

\[\cos \alpha  = \frac{{{x^2} – {y^2}}}{{{z^2}}};\cos \beta  = \frac{{\left| {{y^2} – {z^2}} \right|}}{{{x^2}}};\cos \gamma  = \frac{{{z^2} – {z^2}}}{{{y^2}}}.\]

Lời giải

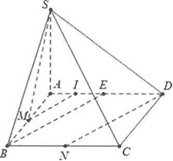
■ Cách 1: Do \[SA \bot \left( {ABCD} \right).\]

Ta có:

\[SA = \sqrt {S{B^2} – A{B^2}}  = a\]. Gọi E là trung điểm của AD và I là trung điểm của AE. Dễ thấy BNDE là hình bình hành và MI là đường trung bình trong tam giác ABE. Khi đó \[DN//BE//MI.\]

Tacó:

\[AM = a;AI = \frac{{AE}}{2} = \frac{a}{2}.\]

Mặt khác:

\[S{M^2} = S{A^2} + A{M^2} = 2{a^2};S{I^2} = \frac{{5{a^2}}}{4}.\]

\[MI = A{I^2} + A{M^2} = \frac{{5{a^2}}}{4}\]. Do vậy \[\cos \widehat {SMI} = \frac{{S{M^2} + M{I^2} – S{I^2}}}{{2.SM.MI}} = \frac{{\sqrt {10} }}{5} = cos(\widehat {SM;DN}).\]

■ Cách 2: Ta có:

\[\overrightarrow {SM} .\overrightarrow {DN} {\rm{ }} = {\rm{ }}\overrightarrow {SM} .\left( {\overrightarrow {SN}  – \overrightarrow {SD} } \right) = \overrightarrow {SM} .\overrightarrow {SN} {\rm{ }} – {\rm{ }}\overrightarrow {SM} .\overrightarrow {SD} \]

\[{\rm{ = }}\frac{1}{2}\left( {S{M^2} + S{N^2} – M{N^2}} \right) – \frac{1}{2}\left( {S{M^2} + S{D^2} – M{D^2}} \right)\]

Mặt khác:

\[S{N^2} = S{A^2} + A{N^2} = S{A^2} + A{B^2} + B{N^2} = 6{a^2},MN = \frac{{AC}}{2} = {\rm{ }}a\sqrt 2 ,S{D^2} = 5{a^2},M{D^2} = 5{a^2}.\]

Do đó

\[\overrightarrow {SM} .\overrightarrow {DN}  = 2{a^2} \Rightarrow \cos \left( {SM;DN} \right) = \frac{{\left| {2{a^2}} \right|}}{{SM.DN}} = \frac{{2{a^2}}}{{a\sqrt 2 .a\sqrt 5 }} = \frac{{\sqrt {10} }}{5}.\]

Lời giải

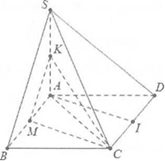
a) Do \[BC//AD \Rightarrow (\widehat {SD;BC}) = (\widehat {SD;AD}) = \widehat {SDA}\]

\[\Delta SAD\] vuông tại A \[ \Rightarrow \cos \widehat {SDA} = \frac{{AD}}{{SD}} = \frac{{AD}}{{\sqrt {A{D^2} + S{A^2}} }} = \frac{1}{{\sqrt 3 }}.\]

b) Gọi M, K lần lượt là trung điểm của AB và SA thì MK là đường trung bình trong tam giác SAB.

Khi đó \[MK//SB\], mặt khác \[MC//AI.\]

Suy ra \[(\widehat {SB;AI}) = (\widehat {MK;CM}).\]

Ta có:

\[MK = \frac{{SB}}{2} = \frac{{\sqrt {S{A^2} + A{B^2}} }}{2} = \frac{{a\sqrt 5 }}{2}\]; \[MC = \sqrt {M{B^2} + B{C^2}}  = \frac{{3a}}{2}\]; \[KC = \sqrt {K{A^2} + A{C^2}}  = 2a.\]

Khi đó

\[cos\widehat {KMC} = \frac{{K{M^2}{\rm{ +  }}M{C^2} – K{C^2}}}{{2.KM.MC}} =  – \frac{1}{{3\sqrt 5 }} \Rightarrow cos\left( {\widehat {SB;AI}} \right) = \frac{1}{{3\sqrt 5 }}.\]

Cách khác: Ta có:

\[\overrightarrow {SB} .\overrightarrow {AI}  = \overrightarrow {SB} .\left( {\overrightarrow {SI}  – \overrightarrow {SA} } \right) = \overrightarrow {SB} .\overrightarrow {SI}  – \overrightarrow {SB} .\overrightarrow {SA} \]

\[ = \frac{1}{2}\left( {S{B^2} + S{I^2} – I{B^2}} \right) – \frac{1}{2}\left( {S{B^2} + S{A^2} – A{B^2}} \right)\]

Do \[S{B^2} = 5{a^2};S{I^2} = S{A^2} + A{D^2} + D{I^2} = \frac{{25{a^2}}}{4};AI = \sqrt {A{D^2} + D{I^2}}  = \frac{{3a}}{2} = IB.\]

Suy ra

\[\overrightarrow {SB} .\overrightarrow {AI}  = \frac{{{a^2}}}{2} \Rightarrow \cos \left( {SB;AI} \right) = \frac{{\left| {\overrightarrow {SB} .\overrightarrow {AI} } \right|}}{{SB.AI}} = \frac{{\frac{{{a^2}}}{2}}}{{a\sqrt 5 .\frac{{3a}}{2}}} = \frac{1}{{3\sqrt 5 }}.\]

Xem thêm