Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây
Tài liệu gồm những nội dung chính sau:
A. Kiến thức cơ bản
B. Bài tập
Bài tập trắc nghiệm nguyên hàm cơ bản – có đáp án và lời giải
Nguyên hàm có bản
A – kiến thức cơ bản
1. Nguyên hàm
Định nghĩa: Cho hàm số \(f(x)\) xác định trên \(K\) ( \(K\) là khoảng, đoạn hay nửa khoảng). Hàm số \(F(x)\) được gọi là nguyên hàm của hàm số \(f(x)\) trên \(K\) nếu \({F^\prime }(x) = f(x)\) với mọi \(x \in K\).
Định lí:
1) Nếu \(F(x)\) là một nguyên hàm của hàm số \(f(x)\) trên \(K\) thì với mỗi hằng số \(C\), hàm số \(G(x) = F(x) + C\) cũng là một nguyên hàm của \(f(x)\) trên \(K\).
2) Nếu \(F(x)\) là một nguyên hàm của hàm số \(f(x)\) trên \(K\) thì mọi nguyên hàm của \(f(x)\) trên \(K\) đều có dạng \(F(x) + C\), với \(C\) là một hằng số.
Do đó \(F(x) + C,C \in \mathbb{R}\) là họ tất cả các nguyên hàm của \(f(x)\) trên \(K\). Ký hiệu \(\int f (x)d{\rm{x}} = F(x) + C\).
2. Tính chất của nguyên hàm
Tính chất 1: \({\left( {\int f (x)d{\rm{x}}} \right)^\prime } = f(x)\) và \(\int {{f^\prime }} (x)d{\rm{x}} = f(x) + C\)
Tính chất 2: \(\int k f(x)d{\rm{x}} = k\int f (x)d{\rm{x}}\) với \(k\) là hằng số khác 0 .
Tính chất 3: \[\smallint [f(x) \pm g(x)]d{\rm{x}} = \smallint f(x)d{\rm{x}} \pm \smallint g(x)d{\rm{x}}\]
3. Sự tồn tại của nguyên hàm
Định lí: Mọi hàm số \(f(x)\) liên tục trên \(K\) đều có nguyên hàm trên \(K\).
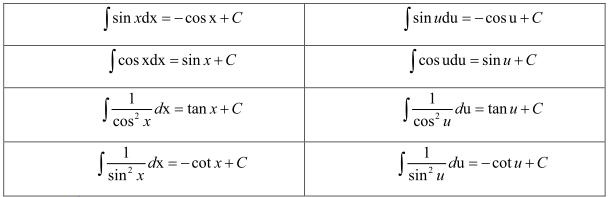
4. Bảng nguyên hàm của một số hàm số sơ cấp

B. Bài tập
Dạng 1 : sử dụng lý thuyết
Câu 1. Trong các khẳng định dưới đây, có bao nhiêu khẳng định đúng?
(1): Mọi hàm số liên tục trên [a ; b] đều có đạo hàm trên [a ; b]
(2): Mọi hàm số liên tục trên [a ; b] đều có nguyên hàm trên [a ; b]
(3): Mọi hàm số liên tục trên [a ; b] đều có nguyên hàm trên [a ; b]
(4): Mọi hàm số liên tục trên [a ; b] đều có giá trị lớn nhất và giá trị nhỏ nhất trên [a ; b].
A. 2 .
B. 3 .
C. 1 .
D. 4 .
Câu 2. Cho hai hàm số \(f(x),g(x)\) liên tục trên \(\mathbb{R}\). Trong các mệnh đề sau, mệnh đề nào sai?
A. \[\smallint [f(x) + g(x)]{\rm{d}}x = \smallint f(x){\rm{d}}x + \smallint g(x){\rm{d}}x\]
B. \[\smallint [f(x) \cdot g(x)]{\rm{d}}x = \smallint f(x){\rm{d}}x \cdot \smallint g(x){\rm{d}}x\]
C. \[\smallint [f(x) – g(x)]{\rm{d}}x = \smallint f(x){\rm{d}}x – \smallint g(x){\rm{d}}x\]
D. \(\int k f(x){\rm{d}}x = k\int f (x){\rm{d}}x(k \ne 0;k \in \mathbb{R})\).
Câu 3. Cho \(f(x),g(x)\) là các hàm số xác định và liên tục trên \(\mathbb{R}\). Trong các mệnh đề sau, mệnh đề nào sai?
A. \(\int f (x)g(x){\rm{d}}x = \int f (x){\rm{d}}x \cdot \int g (x){\rm{d}}x\).
B. \(\int 2 f(x){\rm{d}}x = 2\int f (x){\rm{d}}x\).
C. \[\smallint [f(x) + g(x)]{\rm{d}}x = \smallint f(x){\rm{d}}x + \smallint g(x){\rm{d}}x\]
D. \[\smallint [f(x) – g(x)]{\rm{d}}x = \smallint f(x){\rm{d}}x – \smallint g(x){\rm{d}}x\]
Câu 4. Khẳng định nào sau đây là khẳng định sai?
A. \(\int k f(x){\rm{d}}x = k\int f (x){\rm{d}}x\) với \(k \in \mathbb{R}\).
B. \[\smallint [f(x) + g(x)]{\rm{d}}x = \smallint f(x){\rm{d}}x + \smallint g(x){\rm{d}}x\] với \(f(x);g(x)\) liên tục trên \(\mathbb{R}\).
C. \(\int {{x^\alpha }} {\rm{d}}x = \frac{1}{{\alpha + 1}}{x^{\alpha + 1}}\) với \(\alpha \ne – 1.\)
D. \({\left( {\int f (x){\rm{d}}x} \right)^\prime } = f(x)\).
Câu 5. Cho hai hàm số \(f(x),g(x)\) là hàm số liên tục, có \(F(x),G(x)\) lần lượt là nguyên hàm của \(f(x),g(x)\). Xét các mệnh đề sau:
\((I).F(x) + G(x)\) là một nguyên hàm của \(f(x) + g(x)\).
\((II)\). k.F \((x)\) là một nguyên hàm của \(k.f(x)\) với \(k \in \mathbb{R}\).
\((III) \cdot F(x) \cdot G(x)\) là một nguyên hàm của \(f(x) \cdot g(x)\).
Các mệnh đề đúng là
A. \((II)\) và \((III)\).
B. Cả 3 mệnh đề.
C. \((I)\) và \((III)\).
D. \((I)\) và \((II)\).
Câu 6. Mệnh đề nào sau đây sai?
A. \[\smallint [f(x) – g(x)]dx = \smallint f(x)dx – \smallint g(x)dx\], với mọi hàm số \(f(x),g(x)\) liên tục trên \(\mathbb{R}\).
B. \(\int {{f^\prime }} (x)dx = f(x) + C\) với mọi hàm số \(f(x)\) có đạo hàm trên \(\mathbb{R}\).
C. \[\smallint [f(x) + g(x)]dx = \smallint f(x)dx + \smallint g(x)dx\], với mọi hàm số \(f(x),g(x)\) liên tục trên \(\mathbb{R}\).
D. \(\int k f(x)dx = k\int f (x)dx\) với mọi hằng số \(k\) và với mọi hàm số \(f(x)\) liên tục trên \(\mathbb{R}\).
Câu 7. Cho hàm số \(f(x)\) xác định trên \(K\) và \(F(x)\) là một nguyên hàm của \(f(x)\) trên \(K\). Khẳng định nào dưới đây đúng?
A. \({f^\prime }(x) = F(x),\forall x \in K\).
B. \({F^\prime }(x) = f(x),\forall x \in K\).
C. \(F(x) = f(x),\forall x \in K\).
D. \({F^\prime }(x) = {f^\prime }(x),\forall x \in K\).
Câu 8. Cho hàm số \(f(x)\) xác định trên \(K\). Khẳng định nào sau đây sai?
A. Nếu hàm số \(F(x)\) là một nguyên hàm của \(f(x)\) trên \(K\) thì với mỗi hằng số \(C\), hàm số \(G(x) = F(x) + C\) cũng là một nguyên hàm của \(f(x)\) trên \(K\).
B. Nếu \(f(x)\) liên tục trên \(K\) thì nó có nguyên hàm trên \(K\).
C. Hàm số \(F(x)\) được gọi là một nguyên hàm của \(f(x)\) trên \(K\) nếu \({F^\prime }(x) = f(x)\) với mọi \(x \in K\).
D. Nếu hàm số \(F(x)\) là một nguyên hàm của \(f(x)\) trên \(K\) thì hàm số \(F( – x)\) là một nguyên hàm của \(f(x)\) trên \(K\).
Câu 9. Cho \(f(x) = \frac{1}{{x + 2}}\), chọn mệnh đề sai trong các mệnh đề sau:
A. Trên \(( – 2; + \infty )\), nguyên hàm của hàm số \(f(x)\) là \(F(x) = \ln (x + 2) + {C_1}\); trên khoảng \(( – \infty ; – 2)\), nguyên hàm của hàm số \(f(x)\) là \(F(x) = \ln ( – x – 2) + {C_2}\left( {{C_1},{C_2}} \right.\) là các hằng số).
B. Trên khoảng \(( – \infty ; – 2)\), một nguyên hàm của hàm số \(f(x)\) là \(G(x) = \ln ( – x – 2) – 3\).
C. Trên \(( – 2; + \infty )\), một nguyên hàm của hàm số \(f(x)\) là \(F(x) = \ln (x + 2)\).
D. Nếu \(F(x)\) và \(G(x)\) là hai nguyên hàm của của \(f(x)\) thì chúng sai khác nhau một hằng số.
Câu 10. Khẳng định nào đây sai?
A. \(\int {\cos } x\;{\rm{d}}x = – \sin x + C\).
B. \(\int {\frac{1}{x}} \;{\rm{d}}x = \ln |x| + C\).
C. \(\int 2 x\;{\rm{d}}x = {x^2} + C\).
D. \(\int {{{\rm{e}}^x}} \;{\rm{d}}x = {{\rm{e}}^x} + C\).
Câu 11. Tìm mệnh đề sai trong các mệnh đề sau
A. \(\int {{x^3}} \;{\rm{d}}x = \frac{{{x^4} + C}}{4}\).
B. \(\int {\frac{1}{x}} \;{\rm{d}}x = \ln x + C\).
C. \(\int {\sin } x\;{\rm{d}}x = C – \cos x\).
D. \(\int 2 {{\rm{e}}^x}\;{\rm{d}}x = 2\left( {{{\rm{e}}^x} + C} \right)\).
Câu 12. Trong các khẳng định sau, khẳng định nào sai?
A. \(\int {\rm{d}} x = x + 2C\) ( \(C\) là hằng số).
B.\(\int {{x^n}} \;{\rm{d}}x = \frac{{{x^{n + 1}}}}{{n + 1}} + C(C\) là hằng số \[n \in \mathbb{Z}\])
C. \[\smallint 0{\rm{d}}x = C\](C là hằng số \().\)
D. \(\int {{{\rm{e}}^x}} \;{\rm{d}}x = {{\rm{e}}^x} – C(C\) là hằng số )
Câu 13. Tìm nguyên hàm \(F(x) = \int {{\pi ^2}} \;{\rm{d}}x\).
A. \(F(x) = {\pi ^2}x + C\).
B. \(F(x) = 2\pi x + C\).
C. \(F(x) = \frac{{{\pi ^3}}}{3} + C\).
D. \(F(x) = \frac{{{\pi ^2}{x^2}}}{2} + C\).
Câu 14. Họ nguyên hàm của hàm số \(f(x) = {{\rm{e}}^x} + \cos x + 2018\) là
A. \(F(x) = {{\rm{e}}^x} + \sin x + 2018x + C\).
B. \(F(x) = {{\rm{e}}^x} – \sin x + 2018x + C\).
C. \(F(x) = {{\rm{e}}^x} + \sin x + 2018x\).
D. \(F(x) = {{\rm{e}}^x} + \sin x + 2018 + C\).
Câu 15. Nguyên hàm của hàm số \(f(x) = 2{x^3} – 9\) là:
A. \(\frac{1}{2}{x^4} – 9x + C\).
B. \(4{x^4} – 9x + C\).
C. \(\frac{1}{4}{x^4} + C\).
D. \(4{x^3} – 9x + C\).
Câu 16. Họ nguyên hàm của hàm số \(f(x) = {\rm{e}} \cdot {x^{\rm{e}}} + 4\) là
A. 101376 .
B. \({{\rm{e}}^2} \cdot {x^{{\rm{e}} – 1}} + C\).
C. \(\frac{{{x^{{\rm{e}} + 1}}}}{{{\rm{e}} + 1}} + 4x + C\).
D. \(\frac{{{\rm{ e}}{\rm{. }}{x^{{\rm{e}} + 1}}}}{{{\rm{e}} + 1}} + 4x + C\).
Câu 17. Họ các nguyên hàm của hàm số \(f(x) = 5{x^4} – 6{x^2} + 1\) là
A. \(20{x^3} – 12x + C\).
B. \({x^5} – 2{x^3} + x + C\).
C. \(20{x^5} – 12{x^3} + x + C\).
D. \(\frac{{{x^4}}}{4} + 2{x^2} – 2x + C\).
Câu 18. Khẳng định nào sau đây sai?
A. \(\int 0 \;{\rm{d}}x = C\).
B. \(\int {{x^4}} \;{\rm{d}}x = \frac{{{x^5}}}{5} + C\).
C. \(\int {\frac{1}{x}} \;{\rm{d}}x = \ln x + C\).
D. \(\int {{{\rm{e}}^x}} \;{\rm{d}}x = {{\rm{e}}^x} + C\).
Câu 19. Nguyên hàm của hàm số \(y = {x^2} – 3x + \frac{1}{x}\) là
A. \(\frac{{{x^3}}}{3} – \frac{{3{x^2}}}{2} – \ln |x| + C\)
B. \({\rm{B}}{\rm{. }}\frac{{{x^3}}}{3} – \frac{{3{x^2}}}{2} + \frac{1}{{{x^2}}} + C\)
C. \(\frac{{{x^3}}}{3} – \frac{{3{x^2}}}{2} + \ln x + C\)
D. \(\frac{{{x^3}}}{3} – \frac{{3{x^2}}}{2} + \ln |x| + C\)
Câu 20: Cho hàm số \[f(x) = \frac{a}{{{x^2}}} + \frac{b}{x} + 2\], với a, b là các số hữu tỉ thỏa điều kiện\(\int_{\frac{1}{2}}^1 f (x){\rm{d}}x = 2 – 3\ln 2\)Tính \(T = a + b.\)
A. \(T = – 1\)
B. \(T = 2\).
C. \(T = – 2\)
D. \(T = 0\).
Câu 21. Họ nguyên hàm của hàm số \(f(x) = 3{x^2} + 2x + 5\) là
A. \(F(x) = {x^3} + {x^2} + 5.\)
B. \(F(x) = {x^3} + x + C\).
C. \(F(x) = {x^3} + {x^2} + 5x + C\).
D. \(F(x) = {x^3} + {x^2} + C\).
Câu 22. Hàm số nào sau đây không phải là một nguyên hàm của hàm số \(f(x) = {(3x + 1)^5}\) ?
A. \(F(x) = \frac{{{{(3x + 1)}^6}}}{{18}} + 8\).
B. \(F(x) = \frac{{{{(3x + 1)}^6}}}{{18}} – 2\).
C. \(F(x) = \frac{{{{(3x + 1)}^6}}}{{18}}\).
D. \(F(x) = \frac{{{{(3x + 1)}^6}}}{6}\).
Câu 23. Họ nguyên hàm của hàm số \(f(x) = \frac{1}{{{x^2}}} – {x^2} – \frac{1}{3}\) là
A. \(\frac{{ – {x^4} + {x^2} + 3}}{{3x}} + C\).
B. \(\frac{{ – 2}}{{{x^2}}} – 2x + C\).
C. \( – \frac{{{x^4} + {x^2} + 3}}{{3x}} + C\).
D. \(\frac{{ – {x^3}}}{3} – \frac{1}{x} – \frac{x}{3} + C\).
Câu 24. Họ nguyên hàm của hàm số \(f(x) = 7{x^6} + \frac{1}{x} + \frac{1}{{{x^2}}} – 2\) là
A. \({x^7} + \ln |x| – \frac{1}{x} – 2x\).
B. \({x^7} + \ln |x| + \frac{1}{x} – 2x + C\).
C. \({x^7} + \ln x + \frac{1}{x} – 2x + C\).
D. \({x^7} + \ln |x| – \frac{1}{x} – 2x + C\).
Câu 25. Nguyên hàm của \(f(x) = {x^3} – {x^2} + 2\sqrt x \) là:
A. \(\frac{1}{4}{x^4} – {x^3} + \frac{4}{3}\sqrt {{x^3}} + C\).
B. \(\frac{1}{4}{x^4} – \frac{1}{3}{x^3} + \frac{4}{3}\sqrt {{x^3}} + C\).
C. \(\frac{1}{4}{x^4} – {x^3} + \frac{2}{3}\sqrt {{x^3}} + C\).
D. \(\frac{1}{4}{x^4} – \frac{1}{3}{x^3} + \frac{2}{3}\sqrt {{x^3}} + C\).
Câu 26. Họ nguyên hàm của hàm số \(f(x) = 3\sqrt x + {x^{2018}}\) là
A. \(\sqrt x + \frac{{{x^{2019}}}}{{673}} + C\).
B. \(2\sqrt {{x^3}} + \frac{{{x^{2019}}}}{{2019}} + C\).
C. \(\frac{1}{{\sqrt x }} + \frac{{{x^{2019}}}}{{673}} + C\).
D. \(\frac{1}{{2\sqrt x }} + 6054{x^{2017}} + C\).
Câu 27. Hàm số \(F(x) = {e^x} + \tan x + C\) là nguyên hàm của hàm số \({\rm{f}}({\rm{x}})\) nào
A. \(f(x) = {e^x} – \frac{1}{{{{\sin }^2}x}}\)
B. \(f(x) = {e^x} + \frac{1}{{{{\sin }^2}x}}\)
C. \(f(x) = {e^x}\left( {1 + \frac{{{e^{ – x}}}}{{{{\cos }^2}x}}} \right)\)
D. \(f(x) = {e^x} + \frac{1}{{{{\cos }^2}x}}\)
Câu 28. Nếu \[\smallint f(x){\rm{d}}x = \frac{1}{x} + \ln |2x| + C\] với \[x \in (0; + \infty )\] thì hàm số f(x) là
A. \(f(x) = – \frac{1}{{{x^2}}} + \frac{1}{x}.\)
B. \(f(x) = \sqrt x + \frac{1}{{2x}}\).
C. \(f(x) = \frac{1}{{{x^2}}} + \ln (2x)\).
D. \[f(x) = – \frac{1}{{{x^2}}} + \frac{1}{{2x}}\]
Câu 29. Tìm họ nguyên hàm của hàm số \[f(x) = \frac{{{x^2} – x + 1}}{{x – 1}}\]
A. \(x + \frac{1}{{x – 1}} + C.\)
B. \(1 + \frac{1}{{{{(x – 1)}^2}}} + C\).
C. \[\frac{{{x^2}}}{2} + \ln |x – 1| + C\]
D. \[{x^2} + \ln |x – 1| + C\]
Câu 30. Nguyên hàm \(F(x)\) cula hàm số \(f(x) = 3 – \frac{1}{{{{\sin }^2}}}\) là
A. \(F(x) = 3x – \tan x + C\).
B. \(F(x) = 3x + \tan x + C.\)
C. \(F(x) = 3x + \cot x + C\)
D. \[F(x) = 3x – \cot x + C\]
Câu 31. Tìm nguyên hàm của hàm số \[f(x) = 3\cos x + \frac{1}{{{x^2}}}{\rm{\;tr\^e n\;}}(0; + \infty ){\rm{.\;}}\]
A. \( – 3\sin x + \frac{1}{x} + C\).
B. \(3\sin x – \frac{1}{x} + C\).
C. \(3\cos x + \frac{1}{x} + C\).
D. \(3\cos x + \ln x + C\).
Câu 32. Họ nguyên hàm của hàm số \(f(x) = 3{x^2} + \sin x\) là
A. \({x^3} + \cos x + C\).
B. \({x^3} + \sin x + C\).
C. \({x^3} – \cos x + C\).
D. \(3{x^3} – \sin x + C\).
Câu 33. Tìm nguyên hàm của hàm số \(f(x) = 3{x^2} + 8\sin x\).
A. \(\int f (x){\rm{d}}x = 6x – 8\cos x + C\).
B. \(\int f (x){\rm{d}}x = 6x + 8\cos x + C\).
C. \(\int f (x){\rm{d}}x = {x^3} – 8\cos x + C\).
D. \(\int f (x){\rm{d}}x = {x^3} + 8\cos x + C\).
Câu 34. Tìm nguyên hàm của hàm số \(f(x) = {\cos ^2}\left( {\frac{x}{2}} \right)\)
A. \(\int f (x){\rm{d}}x = x + \sin x + C\).
B. \(\int f (x){\rm{d}}x = x – \sin x + C\).
C. \(\int f (x){\rm{d}}x = \frac{x}{2} + \frac{1}{2}\sin x + C\).
D. \(\int f (x){\rm{d}}x = \frac{x}{2} – \frac{1}{2}\sin x + C\).
Câu 35. Tìm họ nguyên hàm của hàm số \(f(x) = x + \cos x\).
A. \(\int f (x){\rm{d}}x = \frac{{{x^2}}}{2} + \sin x + C\).
B. \(\int f (x){\rm{d}}x = 1 – \sin x + C\).
C. \(\int f (x){\rm{d}}x = x\sin x + \cos x + C\).
D. \(\int f (x){\rm{d}}x = \frac{{{x^2}}}{2} – \sin x + C\).
Câu 36. \(\int {\left( {{x^2} + 2{x^3}} \right)} dx\) có dạng \(\frac{a}{3}{x^3} + \frac{b}{4}{x^4} + C\), trong đó $a, b$ là hai số hữu tỉ. Giá trị \(a\) bằng:
A. 2 .
B. 1 .
C. 9 .
D. 32 .
Câu 37. \(\int {\left( {\frac{1}{3}{x^3} + \frac{{1 + \sqrt 3 }}{5}{x^5}} \right)} dx\) có dạng \(\frac{a}{{12}}{x^4} + \frac{b}{6}{x^6} + C\), trong đó $a, b$ là hai số hữu tỉ. Giá trị \(a\) bằng:
A. 1 .
B. 12 .
C. \(\frac{{36}}{5}(1 + \sqrt 3 )\).
D. Không tồn tại.
Câu 38. \(\int {\left( {(2a + 1){x^3} + b{x^2}} \right)} dx\), trong đó a, b là hai số hữu tỉ. Biết rằng
\(\int {\left( {(2a + 1){x^3} + b{x^2}} \right)} dx = \frac{3}{4}{x^4} + {x^3} + C\). Giá trị a, b lần lượt bằng:
A. 1 ; 3.
B. 3 ; 1.
C. \( – \frac{1}{8};1\).
D.\(\frac{1}{4}x\sin 2x – \frac{1}{2}\cos 2x\)
Câu 39. Tìm nguyên hàm của hàm số \(f(x)\) thỏa mãn điều kiện: \(f(x) = 2x – 3\cos x,F\left( {\frac{\pi }{2}} \right) = 3\)
A. \(F(x) = {x^2} – 3\sin x + 6 + \frac{{{\pi ^2}}}{4}\)
B. \(F(x) = {x^2} – 3\sin x – \frac{{{\pi ^2}}}{4}\)
C. \(F(x) = {x^2} – 3\sin x + \frac{{{\pi ^2}}}{4}\)
D. \(F(x) = {x^2} – 3\sin x + 6 – \frac{{{\pi ^2}}}{4}\)
Câu 40. Một nguyên hàm \({\rm{F}}({\rm{x}})\) của hàm số \(f(x) = 2x + \frac{1}{{{{\sin }^2}x}}\) thỏa mãn \({\rm{F}}\left( {\frac{\pi }{4}} \right) = – 1\) là:
A. \({\rm{F}}(x) = – \cot x + {x^2} – \frac{{{\pi ^2}}}{{16}}\)
B. \({\rm{F}}(x) = \cot x – {x^2} + \frac{{{\pi ^2}}}{{16}}\)
C. \({\rm{F}}(x) = – \cot x + {x^2}\)
D. \({\rm{F}}(x) = – \cot x + {x^2} – \frac{{{\pi ^2}}}{{16}}\)