Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây
44 câu trắc nghiệm mặt cầu – hình cầu – khối cầu – có đáp án chi tiết
MẶT CẦU – HÌNH CẦU – KHỐI CẦU
CÂU HỎI TRẮC NGHIỆM
Câu 1. Một khối cầu tiếp xúc với tất cả các mặt của hình lập phương. Tỉ số thể tích giữa khối cầu và khối lập phương đó bằng:
A. \(\frac{\pi }{3}\)
B. \(\frac{\pi }{6}\)
C. \(\frac{{\pi \sqrt 2 }}{3}\)
D. \(\frac{{2\pi }}{3}\)
Câu 2. Mặt cầu ngoại tiếp hình lập phương cạnh a thì có diện tích bằng:
A. \({a^3}\)
B. \(\frac{{4\pi {a^3}}}{3}\)
C. \(3\pi {a^3}\)
D. \(12\pi {a^2}\sqrt 3 \)
Câu 3. Cho hình lập phương cạnh a nội tiếp trong một mặt cầu. Bán kính đường tròn lớn của mặt cầu đó bằng:
A. \(a\sqrt 3 \)
B. \(a\sqrt 2 \)
C. \(\frac{{a\sqrt 3 }}{2}\)
D. \(\frac{{a\sqrt 2 }}{2}\)
Câu 4. Cho mặt cầu (S ) có tâm A đường kình 10cm và mặt phẳng (P) cách tâm một khoảng 4cm . Kết luận nào sau đây sai ?
A. (P) cắt (S)
B. (P) cắt (S) theo một đường tròn bán kính 3cm
C. (P) tiếp xúc với (S)
D. (P) và (S) có vô số điểm chung
Câu 5. Tỉ số thể tích giữa khối lập phương và khối cầu ngoại tiếp khối lập phương đó là:
A. \(\frac{{2\sqrt 3 }}{{3\pi }}\)
B. \(\frac{{3\pi }}{{2\sqrt 3 }}\)
C. \(\frac{3}{{\pi \sqrt 2 }}\)
D. \(\frac{{\pi \sqrt 2 }}{3}\)
Câu 6. Một hình hộp chữ nhật có 3 kích thước 20cm, \(20\sqrt 3 \)cm, 30cm. Thể tích khối cầu ngoại tiếp hình hộp đó bằng:
A. \(\frac{{32\pi }}{3}d{m^3}\)
B. \(\frac{{62,5\pi }}{3}d{m^3}\)
C. \(\frac{{625000\pi }}{3}d{m^3}\)
D. \(\frac{{3200\pi }}{3}c{m^3}\)
Câu 7. Hình hộp chữ nhật ABCD.A’B’C’D’ có \(BB’ = 2\sqrt 3 cm\), C’B’ = 3cm , diện tích mặt đáy bằng 6cm2 . Thể tích khối cầu ngoại tiếp hình hộp trên bằng: A. \(\frac{{500\pi }}{3}\left( {c{m^3}} \right)\)
B. \(\frac{{125\pi }}{6}\left( {c{m^3}} \right)\)
C. \(100\pi \left( {c{m^3}} \right)\)
D. \(\frac{{100\pi }}{3}\left( {c{m^3}} \right)\)
Câu 8. Cho mặt cầu (S) tâm O bán kính R và điểm A nằm trên (S). Mặt phẳng (P) qua A tạo với OA một góc 600 và cắt (S) theo một đường tròn có diện tích bằng:
A. \(\frac{{3\pi {R^2}}}{4}\)
B. \(\frac{{\pi {R^2}}}{2}\)
C. \(\frac{{3\pi {R^2}}}{2}\)
D. \(\frac{{\pi {R^2}}}{4}\)
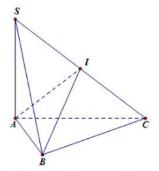
Câu 9. Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, SA vuông góc với mặt phẳng (ABC) và cạnh SA = AB = 10cm. Diện tích mặt cầu ngoại tiếp hình chóp bằng:
A. \(12\pi dm\)
B. \(1200\pi dm\)
C. \(1200\pi d{m^2}\)
D. \(12\pi d{m^2}\)
Câu 10. Cho hình chóp S.ABC SA ^ (ABC), AB = 3cm , góc giữa SB và đáy bằng 600 . Thể tích khối cầu ngoại tiếp hình chóp bằng:
A. \(36\pi c{m^3}\)
B. \(4\pi \sqrt 3 c{m^3}\)
C. \(36\pi c{m^2}\)
D. \(4\pi \sqrt 3 c{m^2}\)
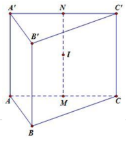
Câu 11. Hình lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác vuông tại B, AA’ = AC = \(a\sqrt 2 \) . Diện tích mặt cầu ngoại tiếp hình lăng trụ bằng:
A. \(8\pi {a^2}\)
B. \(4\pi {a^2}\)
C. \(12\pi {a^2}\)
D. \(10\pi {a^2}\)
Câu 12. Cho hình chóp S.ABCD có đáy là hình vuông, SA ^ (ABCD) và \(SA = AC = 2a\sqrt 2 \). Diện tích mặt cầu ngoại tiếp hình chóp bằng:
A. \(\frac{{16\pi {a^2}}}{3}\)
B. \(\frac{{32\pi {a^2}}}{3}\)
C. \(16\pi {a^2}\)
D. \(8\pi {a^2}\)
Câu 13. Cho hình hộp chữ nhật ABCD.A’B’C’D’ có diện tích các mặt ABCD, ABB’A lần lượt bằng 20cm2, 28cm2, 35cm2. Bán kính mặt cầu ngoại tiếp hình hộp bằng:
A. \(\frac{{3\sqrt {10} }}{2}cm\)
B. \(6\sqrt {10} cm\)
C. \(3\sqrt {10} cm\)
D. 30cm
Câu 14. Cho hình chóp S.ABC có tam giác ABC đều cạnh a = 3cm, SA ^ (ABC) và SA = 2a . Tính thể tích khối cầu ngoại tiếp hình chóp bằng:
A. \(32\pi \sqrt 3 c{m^3}\)
B. \(16\pi \sqrt 3 c{m^3}\)
C. \(\frac{{8{a^3}\pi }}{{3\sqrt 3 }}c{m^3}\)
D. \(\frac{{4\pi {a^3}}}{3}c{m^3}\)
Câu 15. Cho hình chóp S.ABC có tam giác ABC vuông tại A, cạnh BC = 3m, \(SA = 3\sqrt 3 \)và SA ^ (ABC). Thể tích khối cầu ngoại tiếp hình chóp bằng:
A. \(18\pi {m^3}\)
B. \(36\pi {m^3}\)
C. \(16\pi {m^3}\)
D. \(12\pi \sqrt 3 {m^3}\)
Câu 16. Cho hình lăng trụ đều ABC.A’B’C’ có cạnh đáy bằng a , cạnh bên \(AA’ = \frac{{2a}}{3}\). Thể tích khối cầu ngoại tiếp tứ diện ACB’C’ bằng:
A. \(\frac{{4\pi {a^3}}}{{81}}\)
B. \(\frac{{4\pi {a^3}}}{{27}}\)
C. \(\frac{{4\pi {a^3}}}{9}\)
D. \(\frac{{16\pi {a^3}}}{{27}}\)
Câu 17. Hình hộp chữ nhật ABCD.A’B’C’D’ nội tiếp trong mặt cầu bán kính R = 3cm . Tam giác ABC cân và có diện tích bằng 2cm2 . Diện tích toàn phần của hình hộp đó bằng:
A. 8cm 2
B. 24cm2
C. \(8\sqrt {26} c{m^2}\)
D. \(8\left( {1 + \sqrt {26} } \right)c{m^2}\)
Câu 18. Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh đều bằng a . Bán kính của mặt cầu ngoại tiếp hình chóp nói trên bằng:
A. \(R = \frac{{a\sqrt 2 }}{4}\)
B. \(R = \frac{{a\sqrt 2 }}{2}\)
C. \(R = \frac{{a\sqrt 2 }}{3}\)
D. \(R = \frac{{a\sqrt 3 }}{2}\)
Câu 19. Một mặt cầu có đường kính bằng 2a thì có diện tích bằng:
A. \(8\pi {a^2}\)
B. \(\frac{{4\pi {a^2}}}{3}\)
C. \(4\pi {a^2}\)
D. \(16\pi {a^2}\)
Câu 20. Một đường thẳng cắt mặt cầu tâm O tại hai điểm A, B sao cho tam giác OAB vuông cân tại O và \(AB = a\sqrt 2 \). Thể tích khối cầu là:
A. \(V = 4\pi {a^3}\)
B. \(V = \pi {a^3}\)
C. \(V = \frac{4}{3}\pi {a^3}\)
D. \(V = \frac{2}{3}\pi {a^3}\)
Câu 21. Cho mặt cầu (S) có tâm I bán kính R = 5 và mặt phẳng (P) cắt (S) theo một đường tròn (C) có bán kính r = 3 . Kết luận nào sau đây là sai ?
A. Tâm của (C) là hình chiếu vuông góc của I trên (P)
B. (C) là giao tuyến của (S) và (P)
C. Khoảng cách từ I đến (P) bằng 4
D. (C) là đường tròn giao tuyến lớn nhất của (P) và (S)
Câu 22. Cho tứ diện OABC có OA, OB, OC đôi một vuông góc nhau và OA= a, OB = 2a, OC = 3a. Diện tích của mặt cầu (S) ngoại tiếp hình chóp S.ABC bằng: A. \(S = 14\pi {a^2}\)
B. \(S = 8\pi {a^2}\)
C. \(S = 12\pi {a^2}\)
D. \(S = 10\pi {a^2}\)
Câu 23. Thể tích V của một mặt cầu có bán kính R được xác định bởi công thức nào sau đây:
A. \(V = \pi {R^3}\)
B. \(V = 4\pi {R^3}\)
C. \(V = {\frac{{\pi R}}{3}^3}\)
D. \(V = {\frac{{4\pi R}}{3}^3}\)
Câu 24. Cho tứ diện ABCD có DA = 5a và vuông góc với (ABC), DABC vuông tại B và AB = 3a, BC = 4a. Bán kính của mặt cầu nói trên bằng:
A. \(R = \frac{{5a\sqrt 2 }}{2}\)
B. \(R = \frac{{5a\sqrt 3 }}{3}\)
C. \(R = \frac{{5a\sqrt 2 }}{3}\)
D. \(R = \frac{{5a\sqrt 3 }}{2}\)
Câu 25. Cho hình chóp S.ABC có đáy là tam giác ABC vuông tại A, SA ^ (ABC), SA = a, AB = b, AC = c. Bán kính mặt cầu ngoại tiếp hình chóp S.ABC là:
A. \(R = 2\sqrt {{a^2} + {b^2} + {c^2}} \)
B. \(R = \frac{{2\left( {{a^2} + {b^2} + {c^2}} \right)}}{3}\)
C. \(R = \sqrt {{a^2} + {b^2} + {c^2}} \)
D. \(R = \frac{1}{2}\sqrt {{a^2} + {b^2} + {c^2}} \)
Câu 26. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, SA vuông góc với mặt đáy. Bán kính R của mặt cầu ngoại tiếp hình chóp S.ABCD bằng:
A. \(R = \frac{1}{2}AC\)
B. \(R = \frac{1}{2}SB\)
C. \(R = \frac{1}{2}SC\)
D. \(R = \frac{1}{2}SA\)
Câu 27. Trong các khẳng định sau, khẳng định nào sai ?
A. Mặt phẳng (P) tiếp xúc với mặt cầu (S) tâm O tại điểm H thì OH là khoảng cách ngắn nhất từ O đến một điểm bất kỳ nằm trong mặt phẳng (P)
B. Chỉ có duy nhất hai mặt phẳng vuông góc với mặt phẳng cho trước và tiếp xúc với mặt cầu (S).
C. Mặt phẳng cắt mặt cầu (S) theo đường tròn (C) , tâm của đường tròn (C) là hình chiếu của tâm mặt cầu (S) xuống mặt phẳng (P)
D. Tại điểm H nằm trên mặt cầu chỉ có 1 tiếp tuyến duy nhất.
Câu 28. Trong các mệnh đề sau đây, mệnh đề nào sai ?
A. Bất kì một hình tứ diện nào cũng có mặt cầu ngoại tiếp
B. Bất kì một hình hộp chữ nhật nào cũng có một mặt cầu ngoại tiếp
C. Bất kì một hình hộp nào cũng có một mặt cầu ngoại tiếp
D. Bất kì một hình chóp đều nào cũng có một mặt cầu ngoại tiếp
Câu 29. Một mặt cầu có bán kính \(R\sqrt 3 \). Diện tích mặt cầu bằng:
A. \(8\pi {R^2}\)
B. \(12\pi {R^2}\)
C. \(4\pi {R^2}\)
D. \(12\sqrt 3 \pi {R^2}\)
Câu 30. Mặt cầu có bán kính r thì có diện tích là:
A. \(4\pi r\)
B. \(4\pi {r^2}\)
C. \(\frac{4}{3}\pi {r^2}\)
D. \(\frac{4}{3}\pi {r^3}\)
Câu 31. Khối cầu có bán kính r thì có thể tích là:
A. \(4\pi r\)
B. \(4\pi {r^2}\)
C. \(\frac{4}{3}\pi {r^2}\)
D. \(\frac{4}{3}\pi {r^3}\)
Câu 32. Khối cầu có bán kính 3cm thì có thể tích là:
A. \(9\pi \left( {c{m^3}} \right)\)
B. \(36\pi \left( {c{m^3}} \right)\)
C. \(27\pi \left( {c{m^3}} \right)\)
D. \(12\pi \left( {c{m^3}} \right)\)
Câu 33. Mặt cầu có bán kính 4cm thì có diện tích là:
A. \(64\pi \left( {c{m^2}} \right)\)
B. \(16\pi \left( {c{m^2}} \right)\)
C. \(\frac{{64}}{3}\pi \left( {c{m^2}} \right)\)
D. \(\frac{{256}}{3}\pi \left( {c{m^2}} \right)\)
Câu 34. Mặt cầu (S) có diện tích bằng \(100\pi \left( {c{m^2}} \right)\)thì có bán kính là:
A. 3 (cm)
B. 4 (cm)
C. 5 (cm)
D. \(\sqrt 5 \)(cm)
Câu 35. Khối cầu (S) có thể tích bằng \(288\pi \left( {c{m^3}} \right)\)thì có bán kính là:
A. \(6\sqrt 2 \)(cm)
B. 6(cm)
C. \(6\sqrt 6 \) (cm)
D. \(\sqrt 6 \)(cm)
Câu 36. Khối cầu (S) có diện tích bằng \(16\pi {a^2},\left( {a > 0} \right)\)thì có thể tích là:
A. \(\frac{{32}}{3}\pi {a^3}\left( {c{m^3}} \right)\)
B. \(32\pi {a^3}\left( {c{m^3}} \right)\)
C. \(16\pi {a^3}\left( {c{m^3}} \right)\)
D. \(\frac{{16}}{3}\pi {a^3}\left( {c{m^3}} \right)\)
Câu 37. Khối cầu (S1 ) có thể tích bằng \(36\pi \left( {c{m^3}} \right)\)và có bán kính gấp 3 lần bán kính khối cầu (S2 ) . Thể tích của khối cầu (S2 ) là:
A. \(4\pi \left( {c{m^3}} \right)\)
B. \(\frac{4}{3}\pi \left( {c{m^3}} \right)\)
C. \(297\pi \left( {c{m^3}} \right)\)
D. \(324\pi \left( {c{m^3}} \right)\)
Câu 38. Cắt mặt cầu (S) bằng một mặt phẳng đi qua tâm được thiết diện là một hình tròn có chu vi bằng 4p . Diện tích và thể tích của (S) lần lượt là:
A. 16p và \(\frac{{32}}{3}\)p
B. 16p và 32p
C. 8p và \(\frac{{32}}{3}\) p
D. 8p và 32p
Câu 39. Cắt mặt cầu (S) bằng một mặt phẳng cách tâm một khoảng 4cm được thiết diện là một hình tròn có bán kính bằng 3cm. Bán kính của mặt cầu (S) là: A. 5cm
B. 7cm
C. 12cm
D. 10cm
Câu 40. Cắt mặt cầu (S) có bán kính 10 cm bằng một mặt phẳng cách tâm một khoảng 6 cm được thiết diện là hình tròn (C). Diện tích của (C) là:
A. \(16\pi \left( {c{m^2}} \right)\)
B. \(32\pi \left( {c{m^2}} \right)\)
C. \(64\pi \left( {c{m^2}} \right)\)
D. \(128\pi \left( {c{m^2}} \right)\)
Câu 41. Cắt mặt cầu (S) bằng một mặt phẳng cách tâm một khoảng 4cm được thiết diện là hình tròn có diện tích \(9\pi \left( {c{m^2}} \right)\). Thể tích của (S) là:
A. \(\frac{{250}}{3}\pi \left( {c{m^3}} \right)\)
B. \(\frac{{1372}}{3}\pi \left( {c{m^3}} \right)\)
C. \(2304\pi \left( {c{m^3}} \right)\)
D. \(\frac{{500}}{3}\pi \left( {c{m^3}} \right)\)
Câu 42. Mặt cầu ngoại tiếp hình lập phương cạnh 2a có thể tích là:
A. \(3\pi {a^3}\left( {c{m^3}} \right)\)
B. \(\frac{{\sqrt 3 }}{2}\pi {a^3}\left( {c{m^3}} \right)\)
C. \(3\pi {a^3}\left( {c{m^3}} \right)\)
D. \(4\sqrt 3 \pi {a^3}\left( {c{m^3}} \right)\)
Câu 43. Mặt cầu nội tiếp hình lập phương cạnh a có thể tích là:
A. \(\frac{{\pi {a^3}}}{3}\)
B. \(\frac{{\pi {a^3}}}{6}\)
C. \(\frac{{4\pi {a^3}}}{3}\)
D. \(\frac{{4\pi {a^3}}}{9}\)
Câu 44. Mặt cầu ngoại tiếp hình chóp tứ giác đều có tất cả các cạnh bằng 2a thì có bán kính là:
A. \(\frac{{a\sqrt 2 }}{2}\)
B. \(a\sqrt 2 \)
C. a
D. \(\frac{{a\sqrt 3 }}{2}\)
ĐÁP ÁN TRẮC NGHIỆM
|
01. B |
02. C |
03. C |
04. C |
05. A |
06. B |
07.B |
08. D |
09. D |
10. A |
|
11. B |
12. C |
13. A |
14. A |
15. B |
16. A |
17. D |
18. B |
19. C |
20. C |
|
21. D |
22. A |
23. D |
24. A |
25. D |
26. C |
27. D |
28. C |
29. B |
30. B |
|
31. C |
32. B |
33. A |
34. C |
35. B |
36. A |
37. B |
38. A |
39. A |
40. C |
|
41. D |
42. D |
43. B |
44. B |
|
|
|
|
|
|
HƯỚNG DẪN GIẢI
Câu 1. Giả sử cạnh của hình lập phương trình a , khi đó bán kính khối cầu là \(\frac{a}{2}\)Thể tích của khối cầu là \({V_1} = \frac{4}{3}\pi {\left( {\frac{a}{2}} \right)^3} = \frac{{\pi {a^3}}}{6}\)
Thể tích hình lập phương trình \({V_2} = {a^3}.\) Ta cos \(\frac{{{V_1}}}{{{V_2}}} = \frac{\pi }{6}\)
* Chọn B
Câu 2. Ta có \(R = \frac{{a\sqrt 3 }}{2} = > S = 4\pi {\left( {\frac{{a\sqrt 3 }}{2}} \right)^2} = 3\pi {a^2}\)
* Chọn C
Câu 3. Ta có bán kính đường tròn lớn là \(\frac{{a\sqrt 3 }}{2}\)
* Chọn C
Câu 4. Bán kính đường tròn là 5cm, mà d (I,( P)) = 4cm
* Chọn C
Câu 5. Giả sử cạnh của hình lập phương trình a , khi đó bán kính khối cầu là \(\frac{{a\sqrt 3 }}{2}\)
Thể tích khối lập phương là \({V_1} = {a^3}\)
Thể tích khối cầu ngoại tiếp khối lập phương là \({V_2} = \frac{4}{3}\pi {\left( {\frac{{a\sqrt 3 }}{2}} \right)^3} = \frac{{\pi {a^3}\sqrt 3 }}{2}\).
Ta có \(\frac{{{V_1}}}{{{V_2}}} = \frac{{2\sqrt 2 }}{{3\pi }}\)
* Chọn A
Câu 6. Đường kính khối cầu ngoại tiếp là \(\sqrt {{{20}^2} + {{\left( {20\sqrt 3 } \right)}^2} + {{30}^2}} = 50cm\)
=> bán kính R = 25cm = 2,5 dm
Thể tích khối cầu là \(V = \frac{4}{3}\pi {\left( {2,5} \right)^3} = \frac{{62,5}}{3}d{m^3}\)
* Chọn B
Câu 7. Ta có \(A’B’ = \frac{6}{3} = 2cm\) => đường kính khối cầu ngoại tiếp là
\(\sqrt {{{\left( {2\sqrt 3 } \right)}^2} + {3^2} + {2^2}} = 5cm = > R = 2,5cm\)
Thể tích khối cầu ngoại tiếp hình hộp là \(V = \frac{4}{3}\pi {\left( {2,5} \right)^3} = \frac{{125\pi }}{6}c{m^3}\)
*Chọn B
Câu 8. Bán kính đường tròn là \(r = R.\cos {60^0} = \frac{R}{2} = > S = \pi {\left( {\frac{R}{2}} \right)^2} = \frac{{\pi {R^2}}}{4}\)
* Chọn D
Câu 9. Ta có
\(\left\{ {\begin{array}{*{20}{c}}{BC \bot AB}\\{BC \bot SA}\end{array}} \right. \Rightarrow BC \bot \left( {SAB} \right) \Rightarrow BC \bot SB\)
Gọi I là trung điểm của SC => IS = IC = IA = IB (do SAC = SBC = 900 )
Ta có: \(SC = \sqrt {S{A^2} + A{C^2}} = \sqrt {{{10}^2} + {{\left( {10\sqrt 2 } \right)}^2}} = 10\sqrt 3 = > IA = 5\sqrt 3 \)
\( \Rightarrow {S_{mc}} = 4\pi {\left( {5\sqrt 3 } \right)^2} = 1200\pi c{m^2} = 12\pi d{m^2}\)
* Chọn D
Câu 10.
* Chọn A
Câu 11. Gọi M,N lần lượt là trung điểm của AC, A’C’ , I là trung điểm của MN => I là tâm mặt cầu ngoại tiếp hình lăng trụ.
Ta có \(IM = IN = \frac{{a\sqrt 2 }}{2},AB = BC = a\)
=> \(R = IA’ = \sqrt {I{N^2} + N{A^2}} = a = > {S_{mc}} = 4\pi {a^2}\)
* Chọn B
Câu 12. Gọi I là trung điểm của SC => IA = IB = IC = ID = IS
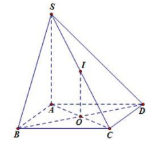
Ta có \(SC = \sqrt {S{A^2} + A{C^2}} = 4a = > IA = 2a\)
=> \({S_{mc}} = 4\pi {\left( {2a} \right)^2} = 16\pi {a^2}\)
*Chọn C
Câu 13. Giả sử AB = a, AD = b, AA’ = c ta có ab = 20, ac = 28, bc =35 => c = 7, b = 5, a = 4. Đường kính mặt cầu ngoại tiếp là \(\sqrt {{a^2} + {b^2} + {c^2}} = 3\sqrt {10} \left( {cm} \right) \Rightarrow R = \frac{{3\sqrt {10} }}{2}\left( {cm} \right)\)
* Chọn A
Câu 14. Gọi G là trọng tâm của DABC Qua G kẻ Gx // SA => Gx ^ (ABC) / / Gọi M là trung điểm của SA, qua M kẻ đường thẳng song song với SA cắt Gx tại I => IA = IB = IC = IS
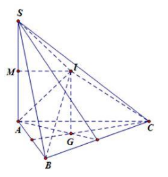
Ta có tứ giác MIGA là hình chữ nhật
\( \Rightarrow IM = AG = \frac{2}{3}.\frac{{a\sqrt 3 }}{2} = \sqrt 3 cm\)
\( \Rightarrow AI = \sqrt {M{A^2} + M{I^2}} = 2\sqrt 3 cm \Rightarrow V = \frac{4}{3}\pi {\left( {2\sqrt 3 } \right)^3} = 32\pi \sqrt 3 c{m^3}\)
* Chọn A
Câu 15. Gọi M là trung điểm của BC, qua M kẻ đường thẳng Mx // SA
=> Mx ^ (ABC)
Gọi N là trung điểm của SA, qua N kẻ đường thẳng vuông góc với SA cắt Mx tại I => IA = IB = IC = IS
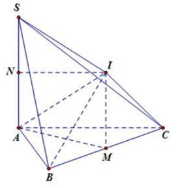
Do tứ giác AMIN là hình chữ nhật \( \Rightarrow NI = AM = \frac{3}{2}cm\)
\( \Rightarrow IA = \sqrt {A{N^2} + N{I^2}} 3cm = > V = \frac{4}{3}\pi {.3^3} = 36\pi c{m^3}\)
* Chọn B
Câu 16. Dễ thấy mặt cầu ngoại tiếp hình lăng trụ đều cũng chính là mặt cầu ngoại tiếp tứ diện ACB’C’
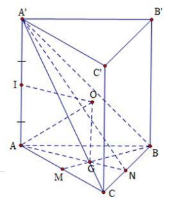
+) Gọi G là trọng tâm tam giác đều ABC, trục đường trong ngoại tiếp DABC cắt mặt phẳng trung trực của AA’ tại O suy ra O là tâm mặt cầu ngoại tiếp khối lăng trụ
Ta có: \(AG = \frac{{a\sqrt 3 }}{3};OG = IA = \frac{a}{3}\)
+) \(R = \sqrt {G{A^2} + O{G^2}} = \sqrt {\frac{{{a^2}}}{3} + \frac{{{a^2}}}{9}} = \frac{{2a}}{3}\)
Do đó \(V = \frac{{4\pi {R^3}}}{3} = \frac{{32\pi {a^3}}}{{81}}\)
*Chọn A
Câu 17. Tam giác ABC vuông tại B suy ra nó vuông cân tại B Khi đó gọi I là tâm của hình vuông ABCD
Ta có \({S_{ABC}} = \frac{{A{B^2}}}{2} = 2 = > AB = 2\)
Do vậy \(IC = \frac{{AC}}{2} = \sqrt 2 = > OI = \sqrt {{R^2} – I{C^2}} = \sqrt {9 – 2} = \sqrt 7 \)
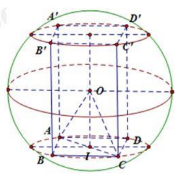
Do đó chiều cao của khối hộp là \(h = 2OI = 2\sqrt 7 \)
\({S_{tp}} = {S_s} + {S_{xq}} = 8 + 8.2\sqrt 7 = 8\left( {1 + \sqrt {28} } \right)\)
* Chọn D
Câu 18. Dựng hình như hình vẽ ta có O là tâm mặt cầu ngoại tiếp của hình chóp. Ta có: \(BD = a\sqrt 2 = > ED = \frac{{a\sqrt 2 }}{2}\)
Khi đó \(\Delta SKO \sim \Delta SED \Rightarrow \frac{{SO}}{{SD}} = \frac{{SK}}{{SE}} \Rightarrow \frac{{SO}}{{SD}} = \frac{{SD}}{{2SE}}\)
Do đó \(SO = R = \frac{{S{D^2}}}{{2SE}} = \frac{{{a^2}}}{{\sqrt[2]{{{a^2} – {{\left( {\frac{a}{{\sqrt 2 }}} \right)}^2}}}}} = \frac{a}{{\sqrt 2 }}\)
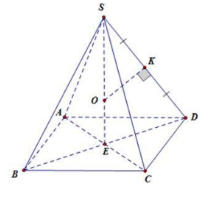
* Chọn B
Câu 19. Ta có: \(d = 2a = > R = \frac{d}{2} = a = > S = 4\pi {R^2} = 4\pi {a^2}\)(với d là đường kính của mặt cầu).
* Chọn C
Câu 20. Dễ thấy \(OA = OB = R = > {R^2} + {R^2} = A{B^2} = 2a = > R = a = > V = \frac{{4\pi {R^3}}}{3} = \frac{{4\pi {a^3}}}{3}\)
* Chọn C.
Câu 21. Ta có: \({R^2} = {r^2} + {d^2}\)(trong đó d = d(I; (P)) suy ra \(d = \sqrt {{R^2} – {r^2}} = 4\). D sai vì đường giao tuyến lớn nhất của (P) và (S) phải đi qua tâm I.
* Chọn D
Câu 22. Gọi M là trung điểm của BC. Khi đó M là tâm đường tròn ngoại tiếp tam giác OBC. Từ M dựng đường thẳng d song song với OA. Trong mặt phẳng (OA; d) dựng đường thẳng trung trực của OA cắt d tại E. Khi đó E là tâm mặt cầu ngoại tiếp của khối chóp.
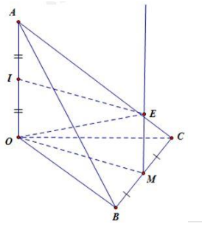
Ta có: \(OM = \frac{{BC}}{2} = \frac{{\sqrt {O{B^2} + O{C^2}} }}{2} = \frac{{a\sqrt {13} }}{2}\)
\(EM = OI = \frac{{OI}}{2} = \frac{a}{2}\)
=> \(R = \sqrt {E{M^2} + O{M^2}} = \frac{{a\sqrt {14} }}{2}\)
Do vậy \(S = 4\pi {R^2} = 14\pi {a^2}\)
* Chọn A
Câu 23. Công thức thể tích khối cầu là \(V = \frac{{4\pi {R^3}}}{3}\)
* Chọn D
Câu 24. Gọi I là trung điểm của AC. Khi đó I là tâm đường trong ngoại tiếp tam giác ABC vuông tại B. Đường thẳng qua I vuông góc với mp(ABC) cắt CD tại O. Khi đó dễ thấy \(OA = OC = OD = \frac{1}{2}CD\)
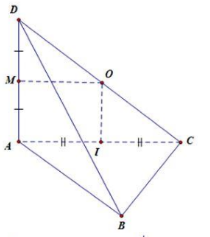
Khi đó \(R = \frac{{CD}}{2} = \frac{{\sqrt {D{A^2} + A{C^2}} }}{2} = \frac{{\sqrt {D{A^2} + A{B^2} + B{C^2}} }}{2} = \frac{{5a\sqrt 2 }}{2}\)
*Chọn A
Câu 25. Gọi M là trung điểm của BC. Khi đó M là tâm đường tròn ngoại tiếp tam giác ABC. Từ M dựng đường thẳng d song song với SA. Trong mặt phẳng (SA;d) dựng đường thẳng trung trực SA cắt d tại O. Khi đó O là tâm mặt cầu ngoại tiếp của khối chóp.
s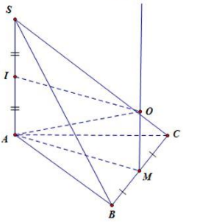
Ta có: \(MA = \frac{1}{2}BC = \frac{1}{2}\sqrt {A{B^2} + A{C^2}} = \frac{{\sqrt {{b^2} + {c^2}} }}{2}\)
Lại có: \(OM = IA = \frac{1}{2}SA = \frac{a}{2}\)
Do vậy \(OA = \sqrt {O{M^2} + M{A^2}} = \frac{{\sqrt {{a^2} + {b^2} + {c^2}} }}{2}\)
* Chọn D
Câu 26. Gọi I là tâm hình chữ nhật ABCD. Từ I dựng đường thẳng song song với SA cắt SC tại O.
Khi đó OA = OB = OC = OD. Mặt khác O là trung điểm của cạnh huyền SC trong tam giác vuông SAC nên SO = OC = OA là tâm mặt cầu ngoại tiếp của hình chóp do vậy \(R = \frac{{SC}}{2}\)
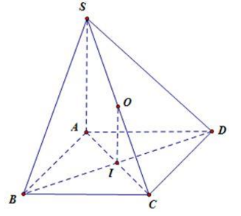
Chọn C
Câu 27. D sai vì tại một điểm H bất kì nằm trên mặt cầu có vô số tiếp tuyến đi qua điểm đó.
* Chọn D
Câu 28. Đáp án C sai vì chỉ có hình hộp chữ nhật mới có mặt cầu ngoại tiếp. Hình hộp xiên hoặc hình hộp có đáy là hình bình hành thì không có mặt cầu ngoại tiếp.
* Chọn C
Câu 29. Ta có \(S = 4\pi {\left( {R\sqrt 3 } \right)^2} = 12\pi \)
* Chọn B
Câu 30. Công thức diện tích mặt cầu bán kính r là \(S = 4\pi {r^2}\)
* Chọn B
Câu 31. Công thức thể tíc khối cầu là \(V = \frac{{4\pi {r^3}}}{3}\)
* Chọn D
Câu 32. Ta có: \(V = \frac{4}{3}\pi {R^3} = 36\pi \)
* Chọn B.
Câu 33. Ta có: \(S = 4\pi {R^2} = 64\pi \)
*Chọn A.
Câu 34. Ta có: \(S = 4\pi {R^2} = 100\pi = > R = 5\)
* Chọn C.
Câu 35. Ta có: \(V = \frac{4}{3}\pi {R^3} = 288\pi = > R = 6\)
* Chọn A
Câu 36. Ta có: \(S = 4\pi {R^2} = 16\pi {a^2} = > R = 2 = > V = \frac{4}{3}\pi {R^3} = \frac{{32\pi {a^3}}}{3}\)
* Chọn A.
Câu 37. Ta có: \({V_{\left( {{S_1}} \right)}} = \frac{{4\pi {R^3}}}{3}\)và \({V_{\left( {{S_2}} \right)}} = {\frac{{4\pi \left( {\frac{R}{3}} \right)}}{3}^3} = \frac{1}{{27}}.\frac{{4\pi {R^3}}}{3} = \frac{{{V_{\left( {{S_1}} \right)}}}}{{27}} = \frac{{4\pi }}{3}\)
*Chọn B
Câu 38. Ta có: \(C = 2\pi r = 4\pi \Rightarrow r = 2\)(với r là bán kính đường tròn thiết diện)
Do thiết diện qua tâm nên \(R = r = 2 \Rightarrow V = \frac{4}{3}\pi {R^3} = \frac{{32}}{3}\pi ;S = 4\pi {R^2} = 16\pi \)
* Chọn A
Câu 39. Ta có: \({R^2} = {r^2} + {d^2} \Rightarrow {R^2} = {4^2} + {3^2} \Rightarrow R = 5\)
* Chọn A
Câu 40. Ta có: \({R^2} = {r^2} + {d^2} \Rightarrow {10^2} = {r^2} + {6^2} \Rightarrow r = 8\)
(với r là bán kính đường tròn (C)) Khi đó \({S_{\left( C \right)}} = \pi {R^2} = 64\pi \)
* Chọn C
Câu 41. Gọi r là bán kính hình tròn là thiết diện của mặt phẳng và mặt cầu (S) Ta có: \(9\pi = \pi {r^2} \Rightarrow r = 3\)
Mặt khác \({R^2} = {r^2} + {d^2} \Rightarrow R = 5 \Rightarrow V = \frac{4}{3}\pi {R^3} = \frac{{500}}{3}\pi \)
* Chọn D
Câu 42. Bán kính mặt cầu ngoại tiếp hình lập phương cạnh 2a là \(R = \frac{{2a\sqrt 3 }}{2} = a\sqrt 3 \)
Do đó \(V = \frac{4}{3}\pi {R^3} = 4\sqrt 3 \pi {a^3}\)
* Chọn D
Câu 43. Bán kính đường tròn nội tiếp hình lập phương là
\({r_{nt}} = \frac{a}{2} \Rightarrow V = \frac{4}{3}\pi {r^3} = \frac{{\pi {a^3}}}{6}\)
* Chọn B
Câu 44. Dựng hình như hình vẽ ta có: \(\Delta SKO \sim \Delta SEG\left( {g – g} \right)\)
Do vậy \(\frac{{SK}}{{SE}} = \frac{{SO}}{{SD}} \Leftrightarrow \frac{{SD}}{{2SE}} = \frac{{SO}}{{SD}} \Rightarrow R = SO = \frac{{S{D^2}}}{{2SE}}\)
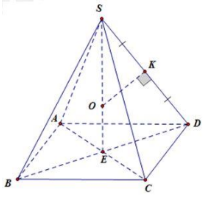
Mặt khác \(SD = AB = 2a \Rightarrow SE = \sqrt {S{D^2} – E{D^2}} = \sqrt 2 \)
Do vậy \(R = a\sqrt 2 \)
Chọn B
Xem thêm