Câu hỏi:
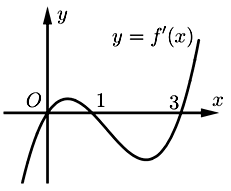
Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(f’\left( x \right)\) liên tục trên \(\mathbb{R}\), đồ thị hàm số \(y = f’\left( x \right)\) như hình vẽ. Biết \(\int\limits_0^3 {\left( {x + 1} \right)f’\left( x \right)d{\rm{x}}} = a\) và \(\int\limits_0^1 {\left| {f’\left( x \right)} \right|d{\rm{x}}} = b\), \(\int\limits_1^3 {\left| {f’\left( x \right)} \right|d{\rm{x}}} = c\), \(f\left( 1 \right) = d\). Tích phân \(\int\limits_0^3 {f\left( x \right)d{\rm{x}}} \) bằng
A. \( – a + b – 3c + 2{\rm{d}}\)
B. \( – a + b – 4c + 3{\rm{d}}\)
Đáp án chính xác
C. \( – a + b + 4c – 5{\rm{d}}\)
D. \( – a – b – 4c + 5{\rm{d}}\)
Trả lời:
Đáp án B
Đặt \(\left\{ \begin{array}{l}u = x + 1\\dv = f’\left( x \right)d{\rm{x}}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}du = d{\rm{x}}\\v = f\left( x \right)\end{array} \right.\) ta có:
\(\int\limits_0^3 {\left( {x + 1} \right)f’\left( x \right)d{\rm{x}}} = \left. {\left( {x + 1} \right)f\left( x \right)} \right|_0^3 – \int\limits_0^3 {f\left( x \right)d{\rm{x}}} = 4f\left( 3 \right) – f\left( 0 \right) – \int\limits_0^3 {f\left( x \right)d{\rm{x}}} = a\).
Mặt khác \(\int\limits_0^1 {\left| {f’\left( x \right)} \right|{\rm{d}}x} = \int\limits_0^1 {f’\left( x \right)dx} = f\left( 1 \right) – f\left( 0 \right) = b \Leftrightarrow f\left( 0 \right) = d – b\).
Lại có \(\int\limits_1^3 {\left| {f’\left( x \right)} \right|{\rm{d}}x} = – \int\limits_1^3 {f’\left( x \right)dx} = f\left( 1 \right) – f\left( 3 \right) = d – f\left( 3 \right) = c \Rightarrow f\left( 3 \right) = d – c\).
Thế vào ta được \(4\left( {d – c} \right) – \left( {d – b} \right) – I = a \Leftrightarrow 3d + b – 4c – a = I.\)
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- \(\lim \frac{{3n + 1}}{{2n – 2}}\) bằng
Câu hỏi:
\(\lim \frac{{3n + 1}}{{2n – 2}}\) bằng
A. \( + \infty \)
B. \( – \infty \)
C. 3
D. \(\frac{3}{2}\)
Đáp án chính xác
Trả lời:
Đáp án D
\(\lim \frac{{3n + 1}}{{2n – 2}} = \lim \frac{{3 + \frac{1}{n}}}{{2 – \frac{2}{n}}} = \frac{3}{2}.\)====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Trong không gian với hệ tọa độ Oxyz, cho hai vectơ \(\overrightarrow a = \left( {2;1;2} \right)\), \(\overrightarrow b = \left( { – 2;1;2} \right)\). Tính \(\cos \left( {\overrightarrow a ,\overrightarrow b } \right)\).
Câu hỏi:
Trong không gian với hệ tọa độ Oxyz, cho hai vectơ \(\overrightarrow a = \left( {2;1;2} \right)\), \(\overrightarrow b = \left( { – 2;1;2} \right)\). Tính \(\cos \left( {\overrightarrow a ,\overrightarrow b } \right)\).
A. \(\frac{1}{3}\)
B. \(\frac{1}{6}\)
C. \(\frac{1}{9}\)
Đáp án chính xác
D. \(\frac{1}{2}\)
Trả lời:
Đáp án C
Ta có \(\cos \left( {\overrightarrow a ;\overrightarrow b } \right) = \frac{{\overrightarrow a .\overrightarrow b }}{{\left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|}} = \frac{{ – 4 + 1 + 4}}{{\sqrt {{2^2} + {1^2} + {2^2}} .\sqrt {{{\left( { – 2} \right)}^2} + {1^2} + {2^2}} }} = \frac{1}{9}\).====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Tập nghiệm của phương trình \({2^{{x^2} – 3{\rm{x}} + 2}} = 4\) là
Câu hỏi:
Tập nghiệm của phương trình \({2^{{x^2} – 3{\rm{x}} + 2}} = 4\) là
A. \(\left\{ 0 \right\}\)
B. \(\left\{ 3 \right\}\)
C. \(\left\{ {0;3} \right\}\)
Đáp án chính xác
D. \(\left\{ {0; – 3} \right\}\)
Trả lời:
Đáp án C
Ta có \({2^{{x^2} – 3x + 2}} = 4 \Leftrightarrow {2^{{x^2} – 3x + 2}} = {2^2} \Leftrightarrow {x^2} – 3x + 2 = 2 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 0}\\{x = 3}\end{array}} \right.\).====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho hình chóp tứ giác S.ABCD có đáy là hình vuông cạnh a, cạnh bên SA vuông góc với mặt phẳng đáy là \(SA = \sqrt 2 a\). Tính thể tích V của khối chóp S.ABCD.
Câu hỏi:
Cho hình chóp tứ giác S.ABCD có đáy là hình vuông cạnh a, cạnh bên SA vuông góc với mặt phẳng đáy là \(SA = \sqrt 2 a\). Tính thể tích V của khối chóp S.ABCD.
A. \(V = \frac{{\sqrt 2 {a^3}}}{6}\)
B. \(V = \frac{{\sqrt 2 {a^3}}}{4}\)
C. \(V = \sqrt 2 {a^3}\)
D. \(V = \frac{{\sqrt 2 {a^3}}}{3}\)
Đáp án chính xác
Trả lời:
Đáp án D
Thể tích khối chóp đã cho là \(V = \frac{1}{3}SA.{S_{ABCD}} = \frac{1}{3}.a\sqrt 2 .{a^2} = \frac{{{a^3}\sqrt 2 }}{3}\).====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho số phức z thỏa mãn \(z\left( {3 + 2i} \right) + 14i = 5\) . Tìm môđun của số phức z.
Câu hỏi:
Cho số phức z thỏa mãn \(z\left( {3 + 2i} \right) + 14i = 5\) . Tìm môđun của số phức z.
A. \(\left| z \right| = \sqrt 7 \)
B. \(\left| z \right| = \sqrt 5 \)
C. \(\left| z \right| = \sqrt {15} \)
D. \(\left| z \right| = \sqrt {17} \)
Đáp án chính xác
Trả lời:
Đáp án D
Ta có \(z\left( {3 + 2i} \right) + 14i = 5 \Leftrightarrow z = \frac{{5 – 14i}}{{3 + 2i}} = – 1 – 4i \Rightarrow \left| z \right| = \sqrt {{{\left( { – 1} \right)}^2} + {{\left( { – 4} \right)}^2}} = \sqrt {17} \).====== **** mời các bạn xem câu tiếp bên dưới **** =====