Câu hỏi:
Cho hàm số \(y = f\left( x \right)\) có đạo hàm trên \(\mathbb{R}\) và \(f’\left( x \right)\) có bảng biến thiên như sau

Hàm số \(g\left( x \right) = f\left( {{x^2} – 2\left| x \right|} \right)\) có nhiều nhất bao nhiêu điểm cực trị
A. 7.
B. 5.
C. 9.
D. 11.
Đáp án chính xác
Trả lời:
Đáp án D
Chú ý \({\left( {\left| x \right|} \right)^\prime } = \frac{x}{{\left| x \right|}}\). Ta có: \(g’\left( x \right) = \left( {2{\rm{x}} – \frac{{2{\rm{x}}}}{{\left| x \right|}}} \right)f’\left( {{x^2} – 2\left| x \right|} \right)\).
Ta có \(2{\rm{x}} – \frac{{2{\rm{x}}}}{{\left| x \right|}} = \frac{{2{\rm{x}}}}{{\left| x \right|}}\left( {\left| x \right| – 1} \right)\) đổi dấu qua 3 điểm \(x = 0,x = \pm 1\).
Phương trình \(f’\left( {{x^2} – 2\left| x \right|} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}{x^2} – 2\left| x \right| = a \in \left( { – \infty ; – 1} \right){\rm{ }}\left( 1 \right)\\{x^2} – 2\left| x \right| = b \in \left( { – 1;0} \right){\rm{ }}\left( 2 \right)\\{x^2} – 2\left| x \right| = c \in \left( {0;1} \right){\rm{ }}\left( 3 \right)\\{x^2} – 2\left| x \right| = d \in \left( {1; + \infty } \right){\rm{ }}\left( 4 \right)\end{array} \right.\)
Nếu coi \(t = \left| x \right|\) thì phương trình (1) vô nghiệm vì \({t^2} – 2t = {\left( {t – 1} \right)^2} – 1 \ge – 1\).
Phương trình (2) có 2 nghiệm \({t_1},{t_2} > 0\) nên có 4 nghiệm x.
Phương trình (3) có 2 nghiệm t trái dấu nên có 2 nghiệm x.
Phương trình (4) có 2 nghiệm t trái dấu nên có 2 nghiệm x.
Do đó hàm số \(y = g\left( x \right)\) có 11 điểm cực trị.
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau
Mệnh đề nào dưới đây sai?
Câu hỏi:
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau
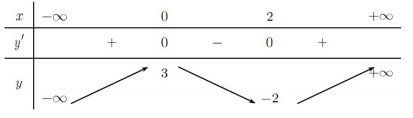
Mệnh đề nào dưới đây sai?A. Hàm số đồng biến trên khoảng \(\left( {2; + \infty } \right).\)
B. Hàm số nghịch biến trên khoảng \(\left( { – \infty ;2} \right).\)
Đáp án chính xác
C. Hàm số nghịch biến trên khoảng \(\left( {0;2} \right).\)
D. Hàm số đồng biến trên khoảng \(\left( { – \infty ;0} \right).\)
Trả lời:
Đáp án B
Từ bảng biến thiên ta có:
Hàm số nghịch biến trên khoảng \(\left( {0;2} \right)\).
Hàm số đồng biến trên khoảng \(\left( { – \infty ;0} \right)\) và \(\left( {2; + \infty } \right)\).
Do đó B là mệnh đề sai.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Trong không gian Oxyz, đường thẳng \(d:\left\{ {\begin{array}{*{20}{l}}{x = 2 – t}\\{y = 1 + 2t}\\{z = 3 + t}\end{array}} \right.\) có một vectơ chỉ phương là
Câu hỏi:
Trong không gian Oxyz, đường thẳng \(d:\left\{ {\begin{array}{*{20}{l}}{x = 2 – t}\\{y = 1 + 2t}\\{z = 3 + t}\end{array}} \right.\) có một vectơ chỉ phương là
A. \(\overrightarrow {{u_3}} = \left( {2;1;3} \right).\)
B. \(\overrightarrow {{u_1}} = \left( { – 1;2;3} \right).\)
C. \(\overrightarrow {{u_2}} = \left( {2;1;1} \right).\)
D. \(\overrightarrow {{u_4}} = \left( { – 1;2;1} \right).\)
Đáp án chính xác
Trả lời:
Đáp án D
Đường thẳng d có một VTCP là \(\overrightarrow u = \left( { – 1;2;1} \right)\).====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Hình nón có bán kính đáy, chiều cao, đường sinh lần lượt là \(r,h,l\). Diện tích xung quanh của hình nón là:
Câu hỏi:
Hình nón có bán kính đáy, chiều cao, đường sinh lần lượt là \(r,h,l\). Diện tích xung quanh của hình nón là:
A. \(S = \pi rh.\)
B. \(S = \pi {r^2}.\)
C. \(S = \pi hl.\)
D. \(S = \pi rl.\)
Đáp án chính xác
Trả lời:
Đáp án D
Diện tích xung quanh của hình nón bằng một nửa tích của độ dài đường tròn đáy và độ dài đường sinh: \(S = \pi r\ell \).====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Số phức liên hợp của \(z = 4 + 3i\) là
Câu hỏi:
Số phức liên hợp của \(z = 4 + 3i\) là
A. \(\bar z = – 3 + 4i.\)
B. \(\bar z = 4 – 3i.\)
Đáp án chính xác
C. \(\bar z = 3 + 4i.\)
D. \(\bar z = 3 – 4i.\)
Trả lời:
Đáp án B
Số phức liên hợp của \(z = 4 + 3i\) là \(\overline z = 4 – 3i\).====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho \(a > 0;b > 0\). Tìm đẳng thức sai.
Câu hỏi:
Cho \(a > 0;b > 0\). Tìm đẳng thức sai.
A. \({\log _2}{\left( {ab} \right)^2} = 2{\log _2}\left( {ab} \right)\)
B. \({\log _2}a + {\log _2}b = {\log _2}\left( {ab} \right)\)
C. \({\log _2}a – {\log _2}b = {\log _2}\frac{a}{b}\)
D. \({\log _2}a + {\log _2}b = {\log _2}\left( {a + b} \right)\)
Đáp án chính xác
Trả lời:
Đáp án D
Sử dụng các công thức:
\({\log _a}x + {\log _a}y = {\log _a}\left( {xy} \right)\)
\({\log _a}x – {\log _a}y = {\log _a}\frac{x}{y}\)
\({\log _{{a^n}}}{b^m} = \frac{m}{n}{\log _a}b\)
\(\left( {0 < a \ne 1;x,y,b > 0} \right)\).
Dựa vào các đáp án ta thấy đáp án D sai.====== **** mời các bạn xem câu tiếp bên dưới **** =====