Câu hỏi:
Cho hình chóp S.ABCD đều có \(AB = 2\) và \(SA = 3\sqrt 2 \). Bán kính của mặt cầu ngoại tiếp hình chóp đã cho bằng
A. \(\frac{7}{4}\)
B. \(\frac{{\sqrt {33} }}{4}\)
C. \(\frac{9}{4}\)
Đáp án chính xác
D. 2.
Trả lời:
Đáp án C
Phương pháp
Xác định tâm mặt cầu ngoại tiếp hình chóp đều là giao của đường trung trực 1 cạnh bên và chiều cao của hình chóp.
Từ đó sử dụng tam giác đồng dạng để tính bán kính mặt cầu ngoại tiếp hình chóp đều
Cách giải
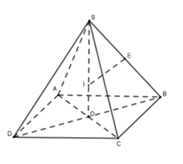
Gọi O là tâm hình vuông ABCD và E là trung điểm SB.
Vì S.ABCD là hình chóp đều nên \(SO \bot \left( {ABCD} \right).\)
Trong \(\left( {SBO} \right)\) kẻ đường trung trực của SB cắt SO tại I, khi đó \(IA = IB = IC = ID = IS\) nên I là tâm mặt cầu ngoại tiếp hình chóp S.ABCD và bán kính mặt cầu là \(R = IS.\)
Ta có ABCD là hình vuông cạnh 2
\( \Rightarrow BD = \sqrt {B{C^2} + C{D^2}} = 2\sqrt 2 \Rightarrow BO = \frac{{BD}}{2} = \sqrt 2 .\)
Ta có \(SA = SB = SC = SD = 3\sqrt 2 \) (vì S.ABCD là hình chóp đều) nên \(SE = EB = \frac{{3\sqrt 2 }}{2}\)
Xét tam giác SBO vuông tại O (vì \(SO \bot \left( {ABCD} \right) \Rightarrow SO \bot OB\)) có \(SO = \sqrt {S{B^2} – O{B^2}} = \sqrt {18 – 2} = 4.\)
Ta có \(\Delta SEI\) đồng dạng với tam giác SOB \(\left( {g – g} \right) \Rightarrow \frac{{SI}}{{SB}} = \frac{{SE}}{{SO}} \Leftrightarrow IS = \frac{{SB.SE}}{{SO}} = \frac{{3\sqrt 2 .\frac{{3\sqrt 2 }}{2}}}{4} = \frac{9}{4}.\)
Vậy bán kính \(R = \frac{9}{4}.\)
Chú ý: Các em có thể sử dụng công thức tính nhanh bán kính mặt cầu ngoại tiếp hình chóp đều có cạnh bên là a và chiều cao h là \(R = \frac{{{a^2}}}{{2h}}.\)
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Trong không gian Oxyz, cho mặt phẳng \(\left( P \right):2x – y + z + 4 = 0\). Khi đó mặt phẳng (P) có một vectơ pháp tuyến là
Câu hỏi:
Trong không gian Oxyz, cho mặt phẳng \(\left( P \right):2x – y + z + 4 = 0\). Khi đó mặt phẳng (P) có một vectơ pháp tuyến là
A. \(\overrightarrow {{n_1}} = \left( {2; – 1;1} \right)\)
Đáp án chính xác
B. \(\overrightarrow {{n_2}} = \left( {2;1;1} \right)\)
C. \(\overrightarrow {{n_4}} = \left( { – 2;1;1} \right)\)
D. \(\overrightarrow {{n_3}} = \left( {2;1;4} \right)\)
Trả lời:
Đáp án A
Phương pháp
Mặt phẳng \(\left( P \right):ax + by + cz + d = 0\) có một vectơ pháp tuyến \(\overrightarrow n = \left( {a;b;c} \right)\)
Cách giải
Mặt phẳng \(\left( P \right):2x – y + z + 4 = 0\) có một VTPT là \(\overrightarrow n = \left( {2; – 1;1} \right).\)====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho a là số thực dương bất kì khác 1. Tính \(S = {\log _a}\left( {{a^3}\sqrt[4]{a}} \right)\).
Câu hỏi:
Cho a là số thực dương bất kì khác 1. Tính \(S = {\log _a}\left( {{a^3}\sqrt[4]{a}} \right)\).
A. \(S = \frac{3}{4}\)
B. \(S = 7\)
C. \(S = \frac{{13}}{4}\)
Đáp án chính xác
D. \(S = 12\)
Trả lời:
Đáp án C
Phương pháp
Sử dụng các công thức lũy thừa thu gọn biểu thức dưới dấu logarit và sử dụng công thức \({\log _a}{a^n} = n.\)
Cách giải
Ta có: \(S = {\log _a}\left( {{a^3}\sqrt[4]{a}} \right) = {\log _a}\left( {{a^3}.{a^{\frac{1}{4}}}} \right) = {\log _a}^{\frac{{13}}{4}} = \frac{{13}}{4}.\)====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho hàm số \(y = f\left( x \right)\) có đạo hàm liên tục trên \(\mathbb{R}\) và có bảng biến thiên như hình bên dưới. Hàm số đã cho đồng biến trên khoảng nào dưới đây?
Câu hỏi:
Cho hàm số \(y = f\left( x \right)\) có đạo hàm liên tục trên \(\mathbb{R}\) và có bảng biến thiên như hình bên dưới. Hàm số đã cho đồng biến trên khoảng nào dưới đây?

A. \(\left( {1; + \infty } \right)\)
B. \(\left( { – 1;0} \right)\)
C. \(\left( { – \infty ;1} \right)\)
D. \(\left( {0;1} \right)\)
Đáp án chính xác
Trả lời:
Đáp án D
Phương pháp
Sử dụng cách đọc bảng biến thiên để suy ra khoảng đồng biến của hàm số.
Hàm số liên tục trên \(\left( {a;b} \right)\) có \(y’ > 0\) với \(x \in \left( {a;b} \right)\) thì hàm số đồng biến trên \(\left( {a;b} \right).\)
Cách giải
Từ BBT ta có hàm số đồng biến trên các khoảng \(\left( { – \infty ; – 1} \right)\) và \(\left( {0;1} \right).\)====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho phương trình \({2^{2x}} – {5.2^x} + 6 = 0\) có hai nghiệm \({x_1},{x_2}\). Tính \(P = {x_1}.{x_2}\).
Câu hỏi:
Cho phương trình \({2^{2x}} – {5.2^x} + 6 = 0\) có hai nghiệm \({x_1},{x_2}\). Tính \(P = {x_1}.{x_2}\).
A. \(P = {\log _2}6\)
B. \(P = 2{\log _2}3\)
C. \(P = {\log _2}3\)
Đáp án chính xác
D. \(P = 6\)
Trả lời:
Đáp án C
Phương pháp
Coi phương trình đã cho là bậc hai ẩn \({2^x}\), giải phương trình tìm x và kết luận.
Cách giải
Ta có: \({2^{2x}} – {5.2^x} + 6 = 0 \Leftrightarrow \left( {{2^x} – 2} \right)\left( {{2^x} – 3} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}{2^x} = 2\\{2^x} = 3\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = {\log _2}3\end{array} \right.\)
Do đó \(P = {x_1}{x_2} = 1.{\log _2}3 = {\log _2}3.\)====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho cấp số cộng có \({u_1} = – 3;{u_{10}} = 24\). Tìm công sai d?
Câu hỏi:
Cho cấp số cộng có \({u_1} = – 3;{u_{10}} = 24\). Tìm công sai d?
A. \(d = \frac{7}{3}\)
B. \(d = – 3\)
C. \(d = – \frac{7}{3}\)
D. \(d = 3\)
Đáp án chính xác
Trả lời:
Đáp án D
Phương pháp
Sử dụng công thức: Cho cấp số cộng có số hạng đầu \({u_1}\) và công sai d thì số hạng thứ \(n\left( {n > 1} \right)\) là
\({u_n} = {u_1} + \left( {n – 1} \right)d.\)
Từ đó ta tìm được công sai d.
Cách giải
Ta có \({u_{10}} = {u_1} + 9d \Leftrightarrow – 3 + 9d = 24 \Leftrightarrow 9d = 27 \Leftrightarrow d = 3.\)====== **** mời các bạn xem câu tiếp bên dưới **** =====