Câu hỏi:
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại \(B,AB = 3a,BC = 4a\). Cạnh bên SA vuông góc với mặt phẳng đáy. Góc tạo bởi giữa SC và mặt phẳng đáy bằng \({60^0}\). Gọi M là trung điểm của AC. Khoảng cách giữa hai đường thẳng AB và SM bằng:
A. \(a\sqrt 3 .\)
B. \(\frac{{10a\sqrt 3 }}{{\sqrt {79} }}.\)
Đáp án chính xác
C. \(5a\sqrt 3 .\)
D. \(\frac{{5a}}{2}.\)
Trả lời:
Đáp án B
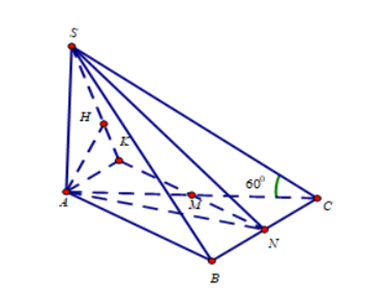
Gọi N là trung điểm của BC. Ta có: \(d\left( {AB;SM} \right) = d\left( {A;\left( {SMN} \right).} \right)\)
Dựng đường cao AK trong tam giác AMN, đường cao AH trong tam giác SAK.
Do \(SA \bot \left( {ABC} \right)\) nên \(SA \bot MN\). (1)
Theo cách dựng ta lại có \(MN \bot AK.\) (2)
Từ (1) và (2) \( \Rightarrow MN \bot AH\) mà \(AH \bot SA\) (theo cách dựng).
\( \Rightarrow AH \bot \left( {SMN} \right)\) tại H nên \(d\left( {AB;SM} \right) = d\left( {A;\left( {SMN} \right)} \right) = AH.\)
Ta có: \(AK = BN = \frac{{BC}}{2} = 2a;AC = 5a.\)
Xét tam giác SAC có \(SA = AC.\tan 60^\circ = 5a\sqrt 3 .\)
Xét tam giác SAK vuông tại A với đường cao AH có:
\(\frac{1}{{A{H^2}}} = \frac{1}{{S{A^2}}} + \frac{1}{{A{K^2}}} = \frac{1}{{75{a^2}}} + \frac{1}{{4{a^2}}} = \frac{{79}}{{300{a^2}}} \Rightarrow A{H^2} = \frac{{300{a^2}}}{{79}} \Rightarrow AH = \frac{{10\sqrt 3 a}}{{\sqrt {79} }}.\)
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Trong không gian Oxyz, cho mặt phẳng \(\left( P \right):2x – y + z + 4 = 0\). Khi đó mặt phẳng (P) có một vectơ pháp tuyến là
Câu hỏi:
Trong không gian Oxyz, cho mặt phẳng \(\left( P \right):2x – y + z + 4 = 0\). Khi đó mặt phẳng (P) có một vectơ pháp tuyến là
A. \(\overrightarrow {{n_1}} = \left( {2; – 1;1} \right)\)
Đáp án chính xác
B. \(\overrightarrow {{n_2}} = \left( {2;1;1} \right)\)
C. \(\overrightarrow {{n_4}} = \left( { – 2;1;1} \right)\)
D. \(\overrightarrow {{n_3}} = \left( {2;1;4} \right)\)
Trả lời:
Đáp án A
Phương pháp
Mặt phẳng \(\left( P \right):ax + by + cz + d = 0\) có một vectơ pháp tuyến \(\overrightarrow n = \left( {a;b;c} \right)\)
Cách giải
Mặt phẳng \(\left( P \right):2x – y + z + 4 = 0\) có một VTPT là \(\overrightarrow n = \left( {2; – 1;1} \right).\)====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho a là số thực dương bất kì khác 1. Tính \(S = {\log _a}\left( {{a^3}\sqrt[4]{a}} \right)\).
Câu hỏi:
Cho a là số thực dương bất kì khác 1. Tính \(S = {\log _a}\left( {{a^3}\sqrt[4]{a}} \right)\).
A. \(S = \frac{3}{4}\)
B. \(S = 7\)
C. \(S = \frac{{13}}{4}\)
Đáp án chính xác
D. \(S = 12\)
Trả lời:
Đáp án C
Phương pháp
Sử dụng các công thức lũy thừa thu gọn biểu thức dưới dấu logarit và sử dụng công thức \({\log _a}{a^n} = n.\)
Cách giải
Ta có: \(S = {\log _a}\left( {{a^3}\sqrt[4]{a}} \right) = {\log _a}\left( {{a^3}.{a^{\frac{1}{4}}}} \right) = {\log _a}^{\frac{{13}}{4}} = \frac{{13}}{4}.\)====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho hàm số \(y = f\left( x \right)\) có đạo hàm liên tục trên \(\mathbb{R}\) và có bảng biến thiên như hình bên dưới. Hàm số đã cho đồng biến trên khoảng nào dưới đây?
Câu hỏi:
Cho hàm số \(y = f\left( x \right)\) có đạo hàm liên tục trên \(\mathbb{R}\) và có bảng biến thiên như hình bên dưới. Hàm số đã cho đồng biến trên khoảng nào dưới đây?

A. \(\left( {1; + \infty } \right)\)
B. \(\left( { – 1;0} \right)\)
C. \(\left( { – \infty ;1} \right)\)
D. \(\left( {0;1} \right)\)
Đáp án chính xác
Trả lời:
Đáp án D
Phương pháp
Sử dụng cách đọc bảng biến thiên để suy ra khoảng đồng biến của hàm số.
Hàm số liên tục trên \(\left( {a;b} \right)\) có \(y’ > 0\) với \(x \in \left( {a;b} \right)\) thì hàm số đồng biến trên \(\left( {a;b} \right).\)
Cách giải
Từ BBT ta có hàm số đồng biến trên các khoảng \(\left( { – \infty ; – 1} \right)\) và \(\left( {0;1} \right).\)====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho phương trình \({2^{2x}} – {5.2^x} + 6 = 0\) có hai nghiệm \({x_1},{x_2}\). Tính \(P = {x_1}.{x_2}\).
Câu hỏi:
Cho phương trình \({2^{2x}} – {5.2^x} + 6 = 0\) có hai nghiệm \({x_1},{x_2}\). Tính \(P = {x_1}.{x_2}\).
A. \(P = {\log _2}6\)
B. \(P = 2{\log _2}3\)
C. \(P = {\log _2}3\)
Đáp án chính xác
D. \(P = 6\)
Trả lời:
Đáp án C
Phương pháp
Coi phương trình đã cho là bậc hai ẩn \({2^x}\), giải phương trình tìm x và kết luận.
Cách giải
Ta có: \({2^{2x}} – {5.2^x} + 6 = 0 \Leftrightarrow \left( {{2^x} – 2} \right)\left( {{2^x} – 3} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}{2^x} = 2\\{2^x} = 3\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = {\log _2}3\end{array} \right.\)
Do đó \(P = {x_1}{x_2} = 1.{\log _2}3 = {\log _2}3.\)====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho cấp số cộng có \({u_1} = – 3;{u_{10}} = 24\). Tìm công sai d?
Câu hỏi:
Cho cấp số cộng có \({u_1} = – 3;{u_{10}} = 24\). Tìm công sai d?
A. \(d = \frac{7}{3}\)
B. \(d = – 3\)
C. \(d = – \frac{7}{3}\)
D. \(d = 3\)
Đáp án chính xác
Trả lời:
Đáp án D
Phương pháp
Sử dụng công thức: Cho cấp số cộng có số hạng đầu \({u_1}\) và công sai d thì số hạng thứ \(n\left( {n > 1} \right)\) là
\({u_n} = {u_1} + \left( {n – 1} \right)d.\)
Từ đó ta tìm được công sai d.
Cách giải
Ta có \({u_{10}} = {u_1} + 9d \Leftrightarrow – 3 + 9d = 24 \Leftrightarrow 9d = 27 \Leftrightarrow d = 3.\)====== **** mời các bạn xem câu tiếp bên dưới **** =====