Câu hỏi:
Có bao nhiêu giá trị nguyên của tham số \(m \in \left[ { – 10;10} \right]\) để bất phương trình sau nghiệm đúng \(\forall x \in \mathbb{R}:{\left( {6 + 2\sqrt 7 } \right)^x} + \left( {2 – m} \right){\left( {3 – \sqrt 7 } \right)^x} – \left( {m + 1} \right){2^x} \ge 0\)?
A. 10.
B. 9.
C. 12.
Đáp án chính xác
D. 11
Trả lời:
Đáp án C
+ Chia cả 2 vế của bất phương trình cho \({2^x} > 0\).
+ Đặt \(t = {\left( {3 + \sqrt 7 } \right)^x}{\rm{ }}\left( {t > 0} \right)\).
+ Đưa bất phương trình về dạng \(m \le f\left( t \right),{\rm{ }}\forall t > 0 \Leftrightarrow m \le \mathop {\min }\limits_{\left( {0; + \infty } \right)} f\left( t \right)\).
+ Lập BBT hàm số \(y = f\left( t \right)\) và kết luận.
Chia cả 2 vế của bất phương trình cho \({2^x} > 0\) ta được: \({\left( {3 + \sqrt 7 } \right)^x} + \left( {2 – m} \right){\left( {\frac{{3 – \sqrt 7 }}{2}} \right)^x} – \left( {m + 1} \right) \ge 0\)
Nhận xét: \({\left( {3 + \sqrt 7 } \right)^x}{\left( {\frac{{3 – \sqrt 7 }}{2}} \right)^x} = 1\), do đó khi ta đặt \(t = {\left( {3 + \sqrt 7 } \right)^x}{\rm{ }}\left( {t > 0} \right) \Rightarrow {\left( {\frac{{3 – \sqrt 7 }}{2}} \right)^x} = \frac{1}{t}\).
Phương trình trở thành: \(t + \left( {2 – m} \right)\frac{1}{t} – \left( {m + 1} \right) \ge 0 \Leftrightarrow {t^2} – \left( {m + 1} \right)t + 2 – m \ge 0\)
\( \Leftrightarrow {t^2} – t + 2 \ge m\left( {t + 1} \right) \Leftrightarrow m \le \frac{{{t^2} – t + 2}}{{t + 1}} = f\left( t \right){\rm{ }}\forall t > 0 \Leftrightarrow m \le \mathop {\min }\limits_{\left( {0; + \infty } \right)} f\left( t \right)\).
Xét hàm số \(f\left( t \right) = \frac{{{t^2} – t + 2}}{{t + 1}}\left( {t > 0} \right)\), ta có: \(f’\left( t \right) = \frac{{\left( {2t – 1} \right)\left( {t + 1} \right) – {t^2} + t – 2}}{{{{\left( {t + 1} \right)}^2}}} = \frac{{{t^2} + 2t – 3}}{{{{\left( {t + 1} \right)}^2}}} = 0 \Leftrightarrow \left[ \begin{array}{l}t = 1\\t = – 3\end{array} \right.\).
BBT:
![Có bao nhiêu giá trị nguyên của tham số m thuộc[-10;10] để bất phương trình sau (ảnh 1)](https://hoc.io.vn/wp-content/uploads/2023/04/blobid8-1657014846.png)
Từ BBT \( \Rightarrow m \le 1\).
Kết hợp điều kiện đề bài \( \Rightarrow \left\{ \begin{array}{l}m \in \mathbb{R}\\m \in \left[ { – 10;1} \right]\end{array} \right. \Rightarrow \) có 12 giá trị của m thỏa mãn yêu cầu bài toán.
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P) đi qua điểm \(A\left( {1; – 1;2} \right)\) và có một vectơ pháp tuyến \(\vec n = \left( {2;2; – 1} \right).\) Phương trình của (P) là
Câu hỏi:
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P) đi qua điểm \(A\left( {1; – 1;2} \right)\) và có một vectơ pháp tuyến \(\vec n = \left( {2;2; – 1} \right).\) Phương trình của (P) là
A. \(2x + 2y – z – 6 = 0.\)
B. \(2x + 2y – z + 2 = 0.\)
Đáp án chính xác
C. \(2x + 2y – z + 6 = 0.\)
D. \(2x + 2y – z – 2 = 0.\)
Trả lời:
Đáp án B
Phương trình \(\left( P \right)\) là: \(2{\rm{x}} + 2y – z + 2 = 0\).====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Đường cong trong hình vẽ bên là đồ thị của hàm số nào trong các hàm số cho dưới đây?
Câu hỏi:
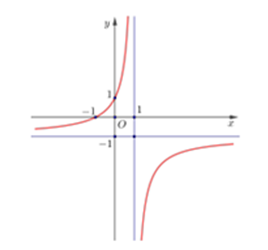
Đường cong trong hình vẽ bên là đồ thị của hàm số nào trong các hàm số cho dưới đây?
A. \(y = \frac{{ – x – 1}}{{x – 1}}\)
Đáp án chính xác
B. \(y = \frac{{x + 1}}{{x – 1}}\)
C. \(y = \frac{{ – x + 1}}{{x + 1}}\)
D. \(y = \frac{{x – 1}}{{x + 1}}\)
Trả lời:
Đáp án A
Đồ thị hàm số có tiệm cận ngang và tiệm cận đứng lần lượt là \(y = 1;x = – 1\).
Ngoài ra hàm số đồng biến trên tập xác định. Chọn A hoặc C.
Tiếp tục tính đạo hàm để loại trừ.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Trong mặt phằng cho 10 điểm phân biệt. Số vectơ khác \(\overrightarrow 0 \), có điểm đầu và điểm cuối lấy trong các điểm đã cho là
Câu hỏi:
Trong mặt phằng cho 10 điểm phân biệt. Số vectơ khác \(\overrightarrow 0 \), có điểm đầu và điểm cuối lấy trong các điểm đã cho là
A. \({2^{10}}\)
B. \(A_{10}^2\)
Đáp án chính xác
C. \(10!\)
D. \(C_{10}^2\)
Trả lời:
Đáp án B
Số vectơ (phân biệt điểm đầu, điểm cuối) là \(A_{10}^2\).====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho hàm số \(y = f\left( x \right)\) có đạo hàm liên tục trên đoạn \(\left[ {0;1} \right]\) và \(f\left( 1 \right) – f\left( 0 \right) = 2\). Tính \(I = \int\limits_0^1 {\left[ {f'\left( x \right) – {e^x}} \right]dx} \).
Câu hỏi:
Cho hàm số \(y = f\left( x \right)\) có đạo hàm liên tục trên đoạn \(\left[ {0;1} \right]\) và \(f\left( 1 \right) – f\left( 0 \right) = 2\). Tính \(I = \int\limits_0^1 {\left[ {f’\left( x \right) – {e^x}} \right]dx} \).
A. \(1 – e\)
B. \(1 + e\)
C. \(3 – e\)
Đáp án chính xác
D. \(3 + e\)
Trả lời:
Đáp án C
\(I = \int\limits_0^1 {f’\left( x \right)d{\rm{x}}} – \int\limits_0^1 {{e^x}d{\rm{x}}} = \left. {f\left( x \right)} \right|_0^1 – \left. {{e^x}} \right|_0^1 = f\left( 1 \right) – f\left( 0 \right) – \left( {e – 1} \right) = 2 – e + 1 = 3 – e\).====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Tập nghiệm của bất phương trình \({3^{2x – 1}} > 27\) là:
Câu hỏi:
Tập nghiệm của bất phương trình \({3^{2x – 1}} > 27\) là:
A. \(\left( {3; + \infty } \right).\)
B. \(\left( {\frac{1}{3}; + \infty } \right).\)
C. \(\left( {\frac{1}{2}; + \infty } \right).\)
D. \(\left( {2; + \infty } \right).\)
Đáp án chính xác
Trả lời:
Đáp án D
\({3^{2{\rm{x}} – 1}} > 27 \Leftrightarrow {3^{2{\rm{x}} – 1}} > {3^3} \Leftrightarrow 2{\rm{x}} – 1 > 3 \Leftrightarrow x > 2\)
Vậy tập nghiệm của bất phương trình là \(\left( {2; + \infty } \right)\).====== **** mời các bạn xem câu tiếp bên dưới **** =====