Câu hỏi:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông, \(AC = \frac{{a\sqrt 2 }}{2}.\) Cạnh bên SA vuông góc với mặt phẳng đáy và đường thẳng SB tạo với mặt phẳng \(\left( {ABCD} \right)\) một góc \(60^\circ .\) Khoảng cách giữa hai đường thẳng \(AD\) và \(SC\) bằng
A. \(\frac{{a\sqrt 3 }}{4}.\)
Đáp án chính xác
B. \(\frac{{a\sqrt 2 }}{2}.\)
C. \(\frac{{a\sqrt 3 }}{2}.\)
D. \(\frac{a}{2}.\)
Trả lời:
Đáp án A
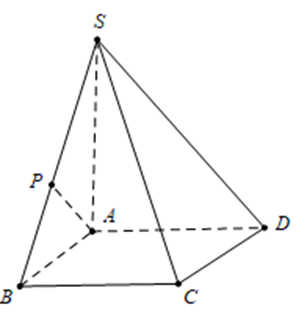
Ta có \(AD//BC \Rightarrow AD//\left( {SBC} \right) \Rightarrow d\left( {AD;SC} \right) = d\left( {A;\left( {SBC} \right)} \right)\).
Kẻ \(AP \bot SB \Rightarrow d\left( {A;\left( {SBC} \right)} \right) = AP \Rightarrow d\left( {AD;SC} \right) = AP\).
Ta có \(\frac{1}{{A{P^2}}} = \frac{1}{{S{A^2}}} + \frac{1}{{A{B^2}}}\). Cạnh \(AB = \frac{{AC}}{{\sqrt 2 }} = \frac{a}{2}\).
Lại có \(\widehat {\left( {SB;\left( {ABCD} \right)} \right)} = \widehat {SBA} = 60^\circ \).
\( \Rightarrow \tan 60^\circ = \frac{{SA}}{{AB}} \Rightarrow SA = \frac{{a\sqrt 3 }}{2} \Rightarrow AP = \frac{{a\sqrt 3 }}{4}.\)
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Trong không gian Oxyz, cho mặt phẳng \(\left( P \right):x + 2y – 3z + 3 = 0.\) Vectơ nào dưới đây là một vectơ pháp tuyến của (P)?
Câu hỏi:
Trong không gian Oxyz, cho mặt phẳng \(\left( P \right):x + 2y – 3z + 3 = 0.\) Vectơ nào dưới đây là một vectơ pháp tuyến của (P)?
A. \(\vec n = \left( {1; – 2;3} \right).\)
B. \(\vec n = \left( {1;2; – 3} \right).\)
Đáp án chính xác
C. \(\vec n = \left( { – 1;2; – 3} \right).\)
D. \(\vec n = \left( {1;2;3} \right).\)
Trả lời:
Đáp án B
Mặt phẳng \(\left( P \right):x + 2y – 3z + 3 = 0\) có một VTPT là \(\overrightarrow n = \left( {1;2; – 3} \right)\).====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho a và b là hai số thực dương tùy ý. Mệnh đề nào dưới đây là đúng?
Câu hỏi:
Cho a và b là hai số thực dương tùy ý. Mệnh đề nào dưới đây là đúng?
A. \(\ln \left( {a{b^3}} \right) = \ln a + \frac{1}{3}\ln b.\)
B. \(\ln \left( {a{b^3}} \right) = \ln a – \frac{1}{3}\ln b.\)
C. \(\ln \left( {a{b^3}} \right) = \ln a + 3\ln b.\)
Đáp án chính xác
D. \(\ln \left( {a{b^3}} \right) = \ln a – 3\ln b.\)
Trả lời:
Đáp án C
Ta có \(\ln \left( {a{b^3}} \right) = \ln a + \ln {b^3} = \ln a + 3\ln b\).====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho hàm số \(f\left( x \right)\) có bảng biến thiên như sau:
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
Câu hỏi:
Cho hàm số \(f\left( x \right)\) có bảng biến thiên như sau:
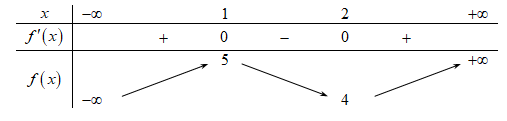
Hàm số đã cho đồng biến trên khoảng nào dưới đây?A. \(\left( {1;2} \right).\)
B. \(\left( { – \infty ;1} \right).\)
Đáp án chính xác
C. \(\left( {1; + \infty } \right).\)
D. \(\left( { – \infty ;5} \right).\)
Trả lời:
Đáp án B
Hàm số \(f\left( x \right)\) đồng biến trên \(\left( { – \infty ;1} \right)\).====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho hàm số \(f\left( x \right)\) có đạo hàm trên đoạn \(\left[ {0;2} \right]\) và \(f\left( 0 \right) = – 1;{\rm{ }}f\left( 2 \right) = 2.\) Tích phân \(\int\limits_0^2 {f'\left( x \right)dx} \) bằng
Câu hỏi:
Cho hàm số \(f\left( x \right)\) có đạo hàm trên đoạn \(\left[ {0;2} \right]\) và \(f\left( 0 \right) = – 1;{\rm{ }}f\left( 2 \right) = 2.\) Tích phân \(\int\limits_0^2 {f’\left( x \right)dx} \) bằng
A. −1.
B. 1.
C. −3.
D. 3.
Đáp án chính xác
Trả lời:
Đáp án D
Ta có \(\int\limits_0^2 {f’\left( x \right)dx} = f\left( x \right)\left| \begin{array}{l}^2\\_0\end{array} \right. = f\left( 2 \right) – f\left( 0 \right) = 3\).====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Tính môđun của số phức z thỏa mãn \(z\left( {1 – i} \right) + 2i = 1.\)
Câu hỏi:
Tính môđun của số phức z thỏa mãn \(z\left( {1 – i} \right) + 2i = 1.\)
A. \(\frac{{\sqrt 5 }}{2}.\)
B. \(\frac{{\sqrt {13} }}{2}.\)
C. \(\frac{{\sqrt {10} }}{2}.\)
Đáp án chính xác
D. \(\frac{{\sqrt {17} }}{2}.\)
Trả lời:
Đáp án C
Ta có \(z = \frac{{1 – 2i}}{{1 – i}} = \frac{3}{2} – \frac{1}{2}i \Rightarrow \left| z \right| = \sqrt {{{\left( {\frac{3}{2}} \right)}^2} + {{\left( { – \frac{1}{2}} \right)}^2}} = \frac{{\sqrt {10} }}{2}\).====== **** mời các bạn xem câu tiếp bên dưới **** =====