Gọi x1, x2 là hai điểm cực trị của hàm số y=x2-4xx+1Tính giá trị của biểu thức P = x1.x2

Câu hỏi:

Gọi x₁, x₂ là hai điểm cực trị của hàm số $y=\frac{x^2–4x}{x+1}$Tính giá trị của biểu thức P = x₁.x₂

A. P = -5

B. P = -2

C. P = -1

D. P = -4

Đáp án chính xác

Trả lời:

Đáp án D

Gọi x₁, x₂ là hoành độ hai điểm cực trị.
Khi đó x₁, x₂ là hai nghiệm của phương trình y’ = 0

Theo định lý Vi-et, ta có x₁.x₂ = -4

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Hàm số nào sau đây đồng biến trên tập số thực R?
   
   

   Câu hỏi:
   

   Hàm số nào sau đây đồng biến trên tập số thực R?

   A. y = x⁴ – 2x² – 5

   B. y = – x + 1

   C.

   D. y = x³ + 3x – 1

   Đáp án chính xác

   Trả lời:

   Chọn D.
   Xét hàm số y = x³ + 3x – 1 có y’ = 3x² + 3 > 0, ∀x ∈ R nên chọn đáp án D.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Trong các hàm số sau, hàm số nào luôn đồng biến trên từng khoảng xác định của nó? y=2x+1x+1(I) ; y = -x4 + x2 – 2 (II); y = x3 – 3x – 5 (III).
   
   

   Câu hỏi:
   

   Trong các hàm số sau, hàm số nào luôn đồng biến trên từng khoảng xác định của nó?
   $y=\frac{2x+1}{x+1}$(I) ; y = -x⁴ + x² – 2 (II); y = x³ – 3x – 5 (III).

   A. I và II

   B. Chỉ I

   Đáp án chính xác

   C. I và III

   D. II và III

   Trả lời:

   Chọn B.
   Hàm số (I): , ∀x ∈ D = R \ {-1} nên hàm số đồng biến trên từng khoảng xác định của nó.
   Hàm số (II): y’ = -4x³ + 2x. y’ = 0 <=> – 4x³ + 2x = 0 <=>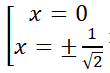  nên hàm số không đồng biến trên khoảng xác định của nó.
    
   Hàm số (III): y’ = 3x² – 3.
   y’ = 0 <=> 3x² – 3 = 0 <=> x = ±1 nên hàm số không đồng biến trên khoảng xác định của nó.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Cho hàm số f(x)=x2-mx-1(m khác 1) Chọn câu trả lời đúng
   
   

   Câu hỏi:
   

   Cho hàm số
   $f\left(x\right)=\frac{x^2–m}{x–1}$(m khác 1)
   Chọn câu trả lời đúng

   A. Hàm số luôn giảm trên (-∞;1) và (1;+∞) với m < 1

   B. Hàm số luôn giảm trên tập xác định.

   C. Hàm số luôn tăng trên (-∞;1) và (1;+∞) với m > 1

   Đáp án chính xác

   D. Hàm số luôn tăng trên (-∞;1) và (1;+∞)

   Trả lời:

   Chọn C.
   Ta có: 
   
   Khi đó với m > 1 thì y’ > 0, ∀x ≠ 1.
   Do đó hàm số luôn tăng trên (-∞;1) và (1;+∞) với m > 1

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Hàm số nào trong các hàm số sau đây đồng biến trên các khoảng (-∞;2) và (2;+∞) 
   
   

   Câu hỏi:
   

   Hàm số nào trong các hàm số sau đây đồng biến trên các khoảng (-∞;2) và (2;+∞) 

   A. 

   Đáp án chính xác

   B .

   C. 

   D. 

   Trả lời:

   Đáp án A
   

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Hàm số nào sau đây nghịch biến trên R.
   
   

   Câu hỏi:
   

   Hàm số nào sau đây nghịch biến trên R.

   A. y = -x³ + 2x² – x – 1

   B. y = 1/3 x³ – x² + 3x + 1

   C. y = -1/3.x³ + x² – x.

   Đáp án chính xác

   D. y = -x³ + 3x + 1

   Trả lời:

   +) Xét hàm số: y = -x³ + 2x² – x – 1\( \Rightarrow y’ =  – 3{x^2} + 4x – 1 = \left( {x – 1} \right)\left( { – 3x + 1} \right)\)+) Xét hàm số: \(y{\rm{ }} = {\rm{ }}\frac{1}{3}{x^3}–{\rm{ }}{x^2} + {\rm{ }}3x{\rm{ }} + {\rm{ }}1\)\( \Rightarrow y’ = {x^2} – 2x + 3 = {\left( {x – 1} \right)^2} + 2 > 0\forall x \in \mathbb{R}\)Suy ra hàm số luôn đồng biến trên \(\mathbb{R}\)+) Xét hàm số: \(y{\rm{ }} = {\rm{ }} – \frac{1}{3}{x^3}{\rm{ +  }}{x^2} – x{\rm{ }}\)\( \Rightarrow y’ =  – {x^2}{\rm{ +  2}}x – 1 =  – {\left( {x – 1} \right)^2} \le 0,\forall x \in \mathbb{R}\)Suy ra hàm số luôn nghịch biến trên \(\mathbb{R}\)+) Xét hàm số y = – x³ + 3x + 1\( \Rightarrow y’ =  – 3{x^2} + 3 =  – 3\left( {x – 1} \right)\left( {x + 1} \right)\)Chọn C

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====