Hình ảnh bên là đồ thị của hàm số nào sau đây?

Câu hỏi:

Hình ảnh bên là đồ thị của hàm số nào sau đây?

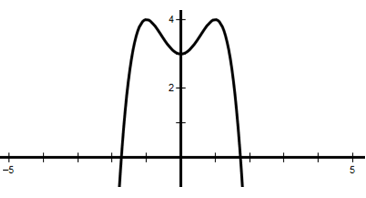
A. y = x⁴ – 2x² – 3

B. y = x⁴ + 2x² – 3

C. y = -x⁴ + 2x² + 3

Đáp án chính xác

D. y = -x⁴ – 2x² + 3

Trả lời:

Đáp án C.
Loại câu A và B vì a = 1 > 0
Đồ thị hàm số đi qua điểm (1;4) thay vào đáp án C và D ta thấy đáp án C thỏa mãn.

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Giá trị lớn nhất và giá trị nhỏ nhất của hàm số y=-x2+6x-5 trên đoạn [1;5] lần lượt là
   
   

   Câu hỏi:
   

   Giá trị lớn nhất và giá trị nhỏ nhất của hàm số $y=\sqrt{–x^2+6x–5}$ trên đoạn [1;5] lần lượt là

   A. 2 và 0

   Đáp án chính xác

   B. 4 và 0

   C. 3 và 0

   D. 0 và -2

   Trả lời:

   Đáp án A.
   
   Vì y(1) = y(5) = 0 và y(3) = 2 nên giá trị lớn nhất và nhỏ nhất của hàm số trên đoạn [1;5] lần lượt là 2 và 0

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số f(x)=2x-46-xtrên đoạn [-3;6]. Tổng M + m có giá trị là
   
   

   Câu hỏi:
   

   Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số $f\left(x\right)=2x–4\sqrt{6–x}$trên đoạn [-3;6]. Tổng M + m có giá trị là

   A. 18

   B. -6

   Đáp án chính xác

   C. -12

   D. -4

   Trả lời:

   Đáp án B
   

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Hàm số y=4-x-x+6 đạt giá trị nhỏ nhất tại x = x0. Tìm x0
   
   

   Câu hỏi:
   

   Hàm số $y=\sqrt{4–x}–\sqrt{x+6}$ đạt giá trị nhỏ nhất tại x = x₀. Tìm x₀

   A. x₀ = -6

   B. x₀ = -1

   C. x₀ = 0  ­

   D. x₀ = 4

   Đáp án chính xác

   Trả lời:

   Đáp án D
   Điểu kiện 
   
   Xét -6 < x < 4, khi đó áp dụng công thức  ta có:
    
   
    
   => hàm số đã cho nghịch biến trên -6 ≤ x ≤ 4
   Vì vậy, hàm số đạt giá trị nhỏ nhất tại x₀ = 4

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Hàm số y=4×2-2x+3+2x-x2 đạt giá trị lớn nhất tại hai giá trị x mà tích của chúng là  
   
   

   Câu hỏi:
   

   Hàm số $y=4\sqrt{x^2–2x+3}+2x–x^2$ đạt giá trị lớn nhất tại hai giá trị x mà tích của chúng là
    

   A. 2

   B. 1

   C. 0.

   D. -1

   Đáp án chính xác

   Trả lời:

   Đáp án D.
   
   
   

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Giá trị nhỏ nhất của hàm số y=6-x-x+4 đạt tại x0, tìm x0?
   
   

   Câu hỏi:
   

   Giá trị nhỏ nhất của hàm số $y=\sqrt{6–x}–\sqrt{x+4}$ đạt tại x₀, tìm x₀?

   A. x₀ = -√10

   B. x₀ = -4

   Đáp án chính xác

   C. x₀ = 6

   D. x₀ = √10

   Trả lời:

   Đáp án B
   

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====