Đường cong hình bên là đồ thị của một hàm số. Hãy chọn khẳng định đúng

Câu hỏi:

Đường cong hình bên là đồ thị của một hàm số. Hãy chọn khẳng định đúng

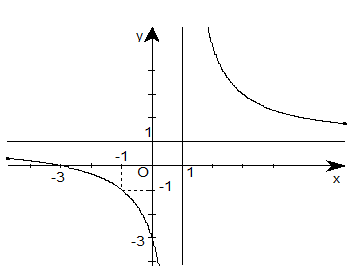
A. Hàm số đồng biến trên các khoảng (-∞; 1) và (1; +∞)

B. Hàm số nghịch biến trên R

C. Hàm số đồng biến trên R

D. Hàm số nghịch biến trên các khoảng (-∞; 1) và (1; +∞)

Đáp án chính xác

Trả lời:

 Đáp án D.
Dựa vào đồ thị ta thấy hàm số nghịch biến trên khoảng (-∞; 1) và (1; +∞).

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Tìm phương trình đường tiệm cận ngang của đồ thị hàm số y=3x+2x+1
   
   

   Câu hỏi:
   

   Tìm phương trình đường tiệm cận ngang của đồ thị hàm số $y=\frac{3x+2}{x+1}$

   A. x = -1.

   B. x = 1.

   C. y = 3.

   Đáp án chính xác

   D. y = 2.

   Trả lời:

   Đáp án C
   

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Đồ thị của hàm số y=x+1×2+2x-3  có bao nhiêu tiệm cận ?
   
   

   Câu hỏi:
   

   Đồ thị của hàm số $y=\frac{x+1}{x^2+2x–3}$  có bao nhiêu tiệm cận ?

   A. 1

   B. 0.

   C. 3

   Đáp án chính xác

   D. 2.

   Trả lời:

    Đáp án C.
   Ta có: D = R \ {1 ; -3}
   

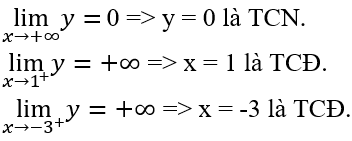
   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Số đường tiệm cận của hàm số y=1-x1+x là
   
   

   Câu hỏi:
   

   Số đường tiệm cận của hàm số $y=\frac{1–x}{1+x}$ là

   A. 0

   B. 1.

   C. 2

   Đáp án chính xác

   D. 3

   Trả lời:

    Đáp án C.
   Hàm số đã cho có tiệm cận đứng là đường thẳng x = -1; tiệm cận ngang là đường thẳng y = -1. Tóm lại là nó có hai đường tiệm cận.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Số tiệm cận của đồ thị hàm số y=2x+1x-2là:
   
   

   Câu hỏi:
   

   Số tiệm cận của đồ thị hàm số $y=\frac{2x+1}{x–2}$là:

   A. 1.

   B. 0

   C. 2.

   Đáp án chính xác

   D. 3.

   Trả lời:

    Đáp án C.
   Ta có   nên đồ thị hàm số có đường tiệm cận ngang là y = 2.
   Và nên đồ thị hàm số có đường tiệm cận đứng là x = 2.
   Vậy đồ thị hàm số có 2 đường tiệm cận.
   Chú ý: đồ thị hàm số   (c ≠ 0; ad – bc ≠ 0) luôn có 2 đường tiệm cận.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Tìm số đường tiệm cận của đồ thị hàm số y=3x-2x
   
   

   Câu hỏi:
   

   Tìm số đường tiệm cận của đồ thị hàm số $y=\frac{3x–2}{x}$

   A. 0

   B. 1

   C. 2.

   Đáp án chính xác

   D. 3

   Trả lời:

   Đáp án C
   
   => Đồ thị có đường tiệm cận ngang y = 3
   
   => Đồ thị có đường tiệm cận đứng x = 0
   Vậy số đường tiệm cận hàm số là 2

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====