Tìm các giá trị của tham số m để đồ thị hàm số y= 2×3+ 3( m-3) x2+ 11- 3m có hai điểm cực trị. Đồng thời hai điểm cực trị đó và điểm C( 0; -1) thẳng hàng

Câu hỏi:

Tìm các giá trị của tham số m để đồ thị hàm số y= 2x³+ 3( m-3) x²+ 11- 3m có hai điểm cực trị. Đồng thời hai điểm cực trị đó và điểm C( 0; -1) thẳng hàng

A. -2

B. -3

C. 3

D. 4

Đáp án chính xác

Trả lời:

Ta có đạo hàm y’ = 6x² + 6( m – 3) x

Hàm số có 2 cực trị khi 3 – m ≠ 0 hay m ≠ 3
Khi đó đồ thị hàm số đã cho có 2 điểm cực trị  A( 0; 11 – 3m) và B( 3 – m; m³ – 9m² + 24m -16) ; $\overrightarrow{AB}=(3–m,{(3–m)}^3).$
Phương trình đt AB: ( 3 – m) ²x+ y -11 + 3m=0
Để 3 điểm A; B; C thẳng hàng khi và chỉ khi C thuộc đường thẳng AB.
Hay : -1 – 11 = 3m = 0 hay m = 4 ™
Chọn D.

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Tìm tất cả các giá trị của tham số thực m để đường thẳng qua 2 điểm cực trị của đồ thị hàm số: y = x3-3mx+ 2  cắt đường tròn tâm I (1; 1)  bán kính bằng 1 tại 2 điểm A và B  mà diện tích tam giác IAB lớn nhất .
   
   

   Câu hỏi:
   

   Tìm tất cả các giá trị của tham số thực m để đường thẳng qua 2 điểm cực trị của đồ thị hàm số: y = x³-3mx+ 2  cắt đường tròn tâm I (1; 1)  bán kính bằng 1 tại 2 điểm A và B  mà diện tích tam giác IAB lớn nhất .

   $A. m = 1\pm \frac{\sqrt{2}}{2}.$

   $B. m = 1\pm \frac{\sqrt{3}}{2}.$

   Đáp án chính xác

   $C. m = 1\pm \frac{\sqrt{5}}{2}$.

   $D. m = 1\pm \frac{\sqrt{6}}{2}.$

   Trả lời:

   Đạo hàm y’ = 3x² – 3m
   
    
   Hàm số có 2 cực trị khi và chỉ khi : m> 0
   Khi đó tọa độ 2 điểm cực trị của đồ thị hàm số là: 
    
   $M(\sqrt{m};–2m\sqrt{m}+2)N(–\sqrt{m}; 2m\sqrt{m}+2) \Rightarrow \overrightarrow{MN}=(–2\sqrt{m};4m\sqrt{m})$
    
   Phương trình đường thẳng MN: 2mx+ y-2=0
   Ta có : 
   $S_{∆IAB}=\frac{1}{2}IA.IB.\sin \widehat{AIB}=\frac{1}{2}\sin \widehat{AIB}\le \frac{1}{2}$
   Dấu bằng xảy ra khi 
   
   Chọn B.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Cho hàm số y= f( x) . Hàm số y= f’ (x) có đồ thị như hình vẽ. Hàm số y= f( x2)  có bao nhiêu khoảng nghịch biến.
   
   

   Câu hỏi:
   

   Cho hàm số y= f( x) . Hàm số y= f’ (x) có đồ thị như hình vẽ.
   
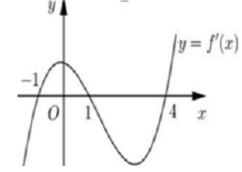
   Hàm số y= f( x²)  có bao nhiêu khoảng nghịch biến.

   A. 5

   B . 3

   Đáp án chính xác

   C. 2

   D. 4

   Trả lời:

   Ta có  g( x) = f( x²) nên g’ (x) = 2x. f’( x²) 
   
   Vậy hàm số đã cho có 3 khoảng nghịch biến.
   Chọn B.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Cho hàm số  y= f( x) ( x-1) liên tục trên R và có đồ thị như hình vẽ. Tìm tất cả các giá trị của tham số m để phương trình f(x) : |x – 1| = m  có số nghiệm lớn nhất
   
   

   Câu hỏi:
   

   Cho hàm số  y= f( x) ( x-1) liên tục trên R và có đồ thị như hình vẽ.
   
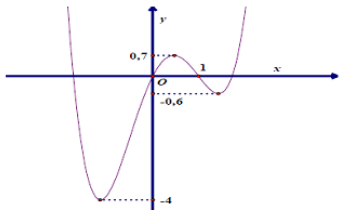
   Tìm tất cả các giá trị của tham số m để phương trình f(x) : |x – 1| = m  có số nghiệm lớn nhất

   A. ( -0, 6; 0]

   B. (-0,6; 0)

   Đáp án chính xác

   C. (0; 0,06)

   D. ( 0; 0,6)

   Trả lời:

   TH1: Với x- 1≥0 hay x≥  1
   khi đó  f(x) |x – 1| = m <=> m = f(x).(x – 1)     (1)
   Dựa vào đồ thị ( C) trên khoảng [1; +∞] để (1) có 2 nghiệm  khi và chỉ khi -0,6< m≤0
   TH2: Với x< 1 khi đó  f(x)|x-1| = m <=> -m = f(x).(x-1)    (2)
   Dựa vào đồ thị (C) trên khoảng $(–\infty ;–1)$ để (1) có 3 nghiệm
   Khi và chỉ khi 0≤ -m <0,7 hay – 0,7< m ≤0
   Kết hợp 2 TH, ta thấy -0,6<m< 0  thì phương trình có tối đa 5 nghiệm ( m= 0 loại vì phương trình có 4 nghiệm).
   Chọn B.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số y=2×3-3( m+1) x2+ 6mx có hai điểm cực trị A; B  sao cho đường thẳng AB vuông góc với đường thẳng y= x+ 2.
   
   

   Câu hỏi:
   

   Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số y=2x³-3( m+1) x²+ 6mx có hai điểm cực trị A; B  sao cho đường thẳng AB vuông góc với đường thẳng y= x+ 2.

   A. 0; 3

   B. 2; 4

   C. 0; 2

   Đáp án chính xác

   D. 1; 3

   Trả lời:

   + Ta có  đạo hàm y’ = 6x²– 6( m + 1)x + 6m
   
   Điều kiện để hàm số có 2 điểm cực trị là : m ≠ 1
   Tọa độ 2 điểm cực trị là A( 1 ; 3m -1) và B ( m ; -m³ + 3m²)
   + Hệ số góc đường thẳng AB là: k = -(m – 1)²
   + Đường thẳng AB vuông góc với đường thẳng y= x + 2 khi và chỉ khi k = -1
   Hay – (m – 1) ² = -1( vì 2 đường thẳng vuông góc với nhau thì tích hai hệ số góc bằng -1) (tm)
   Chọn C.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Cho hàm số y= f( x) =ax4+ bx3+ cx2+ dx+  e và hàm số y= f’( x) có đồ thị như hình vẽ bên. Biết f( b) &lt; 0 , hỏi đồ thị hàm số y= f(x) cắt trục hoành tại nhiều nhất bao nhiêu điểm?
   
   

   Câu hỏi:
   

   Cho hàm số y= f( x) =ax⁴+ bx³+ cx²+ dx+  e và hàm số y= f’( x) có đồ thị như hình vẽ bên. Biết f( b) < 0 , hỏi đồ thị hàm số y= f(x) cắt trục hoành tại nhiều nhất bao nhiêu điểm?
   

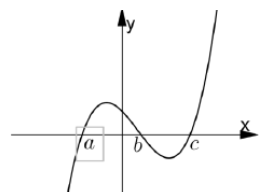
   A. 1

   B. 2

   Đáp án chính xác

   C. 3

   D. 4

   Trả lời:

   Ta có bảng biến thiên như hình vẽ bên.
   Vì f( b) < 0  nên rõ ràng có nhiều nhất 2 giao điểm.
   
   Chọn B.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====