Cho hàm số y=2x+1x-1   có đồ thị C. Gọi M  là một điểm bất kì trên C. Tiếp tuyến của C tại M  cắt các đường tiệm cận của C  tại A và B . Gọi I  là giao điểm của các đường tiệm cận của C . Tính diện tích của tam giác IAB.

Câu hỏi:

Cho hàm số $y=\frac{2x+1}{x–1}$   có đồ thị C. Gọi M  là một điểm bất kì trên C. Tiếp tuyến của C tại M  cắt các đường tiệm cận của C  tại A và B . Gọi I  là giao điểm của các đường tiệm cận của C . Tính diện tích của tam giác IAB.

A. 2

B . 8

C. 6

D. 4

Đáp án chính xác

Trả lời:

Tập xác định D= R\ { 1}.
Đạo hàm $y‘=\frac{–3}{{(x–1)}^2}, \forall x\ne 1.$
Đồ thị hàm số C có tiệm cận đứng là x= 1 và tiệm cận ngang y= 2 nên I (1 ;2 ) là giao của 2  đường tiệm cận.
Gọi $M(x_0; \frac{2x_0+1}{x_0–1})\in \left(C\right), x_0\ne 1.$
Tiếp tuyến ∆ của C  tại M  có phương trình là :
$\iff y=\frac{–3}{{(x_0–1)}^2}(x–x_0)+\frac{2x_0+1}{x_0–1}$
∆ cắt TCĐ tại $A(1; \frac{2x_0+2}{x_0–1})$  và cắt TCN  tại B( 2x₀-1 ; 2)  .
Ta có $IA=\left|\frac{2x_0+2}{x_0–1}–2\right|=\frac{4}{\left|x_0–1\right|}; IB=\left|(2x_0–1)–1\right|=2\left|x_0–1\right|.$
Do đó,  $S=\frac{1}{2}IA.IB=\frac{1}{2}\frac{4}{\left|x_0–1\right|}.2\left|x_0–1\right|=4$.
Chọn D.

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Tìm m để giá trị lớn nhất của hàm số y=x2+2x+m-4  trên đoạn [-2; 1]  đạt giá trị nhỏ nhất. Giá trị của m là
   
   

   Câu hỏi:
   

   Tìm m để giá trị lớn nhất của hàm số $y=\left|x^2+2x+m–4\right|$  trên đoạn [-2; 1]  đạt giá trị nhỏ nhất. Giá trị của m là

   A. 4

   B. 3

   Đáp án chính xác

   C. 1

   D. 2

   Trả lời:

   $y=\left|x^2+2x+m–4\right|=\left|{(x+1)}^2+m–5\right|$
   Ta có: ${(x+1)}^2+m–5 \ge m – 5 \forall m$
   ${(x+1)}^2+m–5= m – 1$ với m = 1
    Suy ra: $\left[{(x+1)}^2+m–5\right]\in \left[m–5;m–1\right]$
   Giá trị lớn nhất của hàm số  $y=\left|x^2+2x+m–4\right|$ trên đoạn[ -2; 1] đạt giá trị nhỏ nhất khi
    $\left\{\begin{array}{l}m–5<0\\ \begin{array}{c}m–1>0\\ 5–m=m–1\end{array}\end{array}\right.\iff m=3$
   Chọn B.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số  y= x3-3mx2+ 3m3 có hai điểm cực trị A và B  sao cho tam giác OAB  có diện tích bằng 48.
   
   

   Câu hỏi:
   

   Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số  y= x³-3mx²+ 3m³ có hai điểm cực trị A và B  sao cho tam giác OAB  có diện tích bằng 48.

   A.  m= 1.

   B . m = 2

   C. m= -2

   D. Đáp án khác

   Đáp án chính xác

   Trả lời:

   + Đạo  hàm y’ = 3x²– 6mx= 3x( x- 2m)
   
    
   Đồ thị hàm số có hai điểm cực trị khi và chỉ khi :m≠0.   (1)                             
   + Tọa độ các điểm cực trị của đồ thị hàm số là  A( 0 ; 3m³) ; B( 2m; -m³)   
   Ta có: $\overrightarrow{OA}(0;3m^3)\Rightarrow OA=3\left|m^3\right| \left(2\right)$
   Ta thấy $A\in Oy\Rightarrow OA\equiv Oy\Rightarrow d(B;OA)=d(B;Oy)=2\left|m\right|$                (3)
   + Từ (2) và (3) suy ra  S= ½. OA.d(B ; OA)=3m⁴.
   Do đó: $S_{∆OAB}=48\iff 3m^4=48\iff m=\pm 2$ (thỏa mãn (1) ).
    
   Chọn D.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Cho hàm số y= x4-2( m+1)x2+ m ( C). Tìm tất cả các giá trị thực của tham số m  để đồ thị hàm số C có ba điểm cực trị A: B; C  sao cho  OA= BC ;   trong đó O  là gốc tọa độ,  A là điểm cực trị thuộc trục tung, B và C là hai điểm cực trị còn lại.
   
   

   Câu hỏi:
   

   Cho hàm số y= x⁴-2( m+1)x²+ m ( C). Tìm tất cả các giá trị thực của tham số m  để đồ thị hàm số C có ba điểm cực trị A: B; C  sao cho  OA= BC ;   trong đó O  là gốc tọa độ,  A là điểm cực trị thuộc trục tung, B và C là hai điểm cực trị còn lại.

   A. $m=2\pm 2\sqrt{2}$

   Đáp án chính xác

   B. $m=2+2\sqrt{2}$

   C. $m=2–2\sqrt{2}$

   D. $m=\pm 1$

   Trả lời:

   Ta có : y’ = 4x³-4( m+ 1) x= 4x( x²– (m+ 1) ).
   Hàm số có 3 điểm cực trị khi và chỉ khi y’ = 0 có 3 nghiệm phân biệt hay m + 1> 0 suy ra m > – 1. (*)
   Khi đó, ta có: 
   
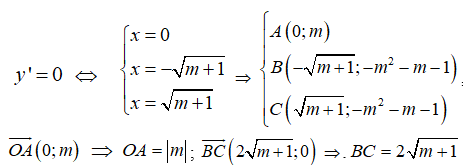
   Do đó $OA=BC\iff \left|m\right|=2\sqrt{m+1}\iff m^2–4m–4=0(∆‘=8)\iff m=2\pm 2\sqrt{2}$ (thỏa mãn (*).
   Vậy $m=2\pm 2\sqrt{2}.$
   Chọn  A.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Tìm tất cả các giá trị thực của tham số m  để đồ thị hàm số  y= x3- 3mx2+ 4m3   có các điểm cực đại và cực tiểu đối xứng nhau qua đường thẳng x- y=0.
   
   

   Câu hỏi:
   

   Tìm tất cả các giá trị thực của tham số m  để đồ thị hàm số  y= x³– 3mx²+ 4m³   có các điểm cực đại và cực tiểu đối xứng nhau qua đường thẳng x- y=0.

   A. $m=\frac{\sqrt{2}}{2}$

   B. $m=–\frac{\sqrt{2}}{2}$

   C. m=0 hoặc $m=\frac{\sqrt{2}}{2}$

   D. $m=\pm \frac{\sqrt{2}}{2}$

   Đáp án chính xác

   Trả lời:

   + Đạo hàm : y’ = 3x²– 6mx
   
    
   Để hàm số có cực đại và cực tiểu thì m≠ 0.
   + Giả sử hàm số có hai điểm cực trị là:  A( 0; 4m³) ; B( 2m; 0) ;  $\overrightarrow{AB}=(2m;–4m^3)$
   Trung điểm của đoạn AB là   I (m; 2m³).
   + Điều kiện để  đối xứng nhau qua đường thẳng x- y= 0 hay y= x  là AB vuông góc với đường thẳng y= x  và $I\in \left(d\right)\iff \left\{\begin{array}{l}2m–4m^3=0\\ 2m^3=m\end{array}\right.$
   $\iff m=0 hoặc m=\pm \frac{\sqrt{2}}{2}$
    
   Kết hợp với điều kiện ta có: $m=\pm \frac{\sqrt{2}}{2}.$
   Chọn D.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Tính tổng tất cả các giá trị thực của tham số m để hàm số y= x3-3mx2+ 3( m2-1) x- m3+ m  có cực trị, đồng thời khoảng cách từ điểm cực đại của đồ thị hàm số đến gốc tọa độ O bằng 2 lần khoảng cách từ điểm cực tiểu của đồ thị hàm số đến gốc tọa độ O.  
   
   

   Câu hỏi:
   

   Tính tổng tất cả các giá trị thực của tham số m để hàm số y= x³-3mx²+ 3( m²-1) x- m³+ m  có cực trị, đồng thời khoảng cách từ điểm cực đại của đồ thị hàm số đến gốc tọa độ O bằng $\sqrt{2}$ lần khoảng cách từ điểm cực tiểu của đồ thị hàm số đến gốc tọa độ O.
    

   A. -4

   B. -5

   C. -6.

   Đáp án chính xác

   D. -7

   Trả lời:

   Ta có y’ = 3x²– 6mx + 3( m²-1).
   Hàm số đã cho  có cực trị thì phương trình y’ =0  có 2 nghiệm phân biệt
   $\iff x^2–2mx+m^2–1=0$có 2 nghiệm phân biệt $\iff ∆‘=1>0,\forall m$  
   Khi đó, điểm cực đại  A( m-1; 2-2m) và điểm cực tiểu  B( m+1; -2-2m)
   Ta có 
   
   Tổng hai giá trị này là -6.
   Chọn C.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====