Tính tổng phần ảo các số phức z thỏa mãn |z| = 5 và phần thực của nó bằng 2 lần phần ảo.

Câu hỏi:

Tính tổng phần ảo các số phức z thỏa mãn |z| = 5 và phần thực của nó bằng 2 lần phần ảo.

A. 0

Đáp án chính xác

B. 1

C. 2

D.3

Trả lời:

Chọn A.
Gọi số phức cần tìm là z = x + yi.
Ta có:
 hay x² + y² = 25     (*)
Mặt khác: Số phức có phần thực của nó bằng 2 lần phần ảo nên x = 2y
thay vào phương trình (*) ta được: 5y² = 25 hay  
Vậy số phức cần tìm là: 
Do đó tổng các phần ảo là: $\sqrt{5}+\left(–\sqrt{5}\right)=0$

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Trên mặt phẳng tọa độ Oxy, tìm tập hợp các điểm biểu diễn các số phức z  thỏa mãn điều kiện |z – 2| + |z + 2| = 10.
   
   

   Câu hỏi:
   

   Trên mặt phẳng tọa độ Oxy, tìm tập hợp các điểm biểu diễn các số phức z  thỏa mãn điều kiện |z – 2| + |z + 2| = 10.

   A. Đường tròn ( x – 2) ² + ( y + 2) ² = 100.

   B. Elip 

   C. Đường tròn  ( x -2) ² + ( y + 2) ² = 10.

   D. Elip 

   Đáp án chính xác

   Trả lời:

   Chọn D.
   Gọi M(x; y)  là điểm biểu diễn số phức z = x + yi, x, y ∈ R
   Gọi A là điểm biểu diễn số phức 2
   Gọi B là điểm biểu diễn số phức -2
   Ta có: |z – 2| + |z + 2| = 10 ⇔ MB + MA = 10.
   Ta có AB = 4.
   Suy ra tập hợp điểm M biểu diễn số phức z là Elip với 2 tiêu điểm là A(2; 0), B( -2; 0)  tiêu cự  AB = 4 = 2c, độ dài trục lớn là 10 = 2a , độ dài trục bé là 
   Vậy tập hợp các điểm biểu diễn các số phức z thỏa mãn điều kiện |z – 2| + |z + 2| = 10 là elip có phương trình 

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Cho số phức z  thỏa mãn |z + 2| + |z – 2| = 8. Trong mặt phẳng phức tập hợp những điểm M biểu diễn cho số phức z  là?
   
   

   Câu hỏi:
   

   Cho số phức z  thỏa mãn |z + 2| + |z – 2| = 8. Trong mặt phẳng phức tập hợp những điểm M biểu diễn cho số phức z  là?

   

   Đáp án chính xác

   

   C. ( x + 2) ² + ( y – 2) ² = 64.

   D. ( x + 2) ² + ( y – 2) ² = 8.

   Trả lời:

   Chọn A.
    
   Gọi M(x; y) , F₁= ( -2; 0) và F₂( 2; 0).
   Ta có |z + 2| + |z – 2| = 8 
   $\iff \sqrt{{\left(x+2\right)}^2+y^2}+\sqrt{{\left(x–2\right)}^2+y^2}=8$
   Hay MF₁+ MF₂ = 8.
   Do đó điểm M(x; y)  nằm trên elip (E ) có 2a = 8 nên a = 4
   ta có F₁F₂ = 2c nên 4 = 2c  hay c = 2
   Ta có b² = a² – c² = 16 – 4 = 12
   Vậy tập hợp các điểm M là elip 

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Tìm nghiệm của phương trình:
   
   

   Câu hỏi:
   

   Tìm nghiệm của phương trình:

   

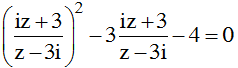
   B.  Không có z thỏa mãn

   Đáp án chính xác

   

   

   Trả lời:

   Chọn B.
   Điều kiện: z $\ne$ 3i
   Đặt . Phương trình đã cho trở thành: t² – 3t – 4 = 0
   Suy ra: t = 4 hoặc t = -1
   Với t = 4 thì 
   Hay iz + 3 = 4( z – 3i)
   $\iff \left(–4+i\right)z=–12i–3\iff z= \frac{–12i–3}{–4+i}=3i$
   Không thỏa mãn.
   Với t = -1 thì 
   Suy ra: iz + 3 =  -1 ( z – 3i)
   ( 1 + i) z = -3 + 3i hay z = 3i (không thỏa mãn)
   Vậy không có z thỏa mãn.
    

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Tìm nghiệm của phương trình: ( z + 3 – i)2 – 6( z + 3 – i) + 13 = 0
   
   

   Câu hỏi:
   

   Tìm nghiệm của phương trình: ( z + 3 – i)² – 6( z + 3 – i) + 13 = 0

   A. z = 3i; z = 1 – 2i

   B. z = – i; z = 3i + 4

   C. z = 3i + 4; z = 3i

   D. z = 3i; z = -i

   Đáp án chính xác

   Trả lời:

   Chọn  D.
   Đặt t = z + 3 – i. Phương trình đã cho trở thành: t² – 6t + 13 = 0
   Suy ra :  t = 3 + 2i hoặc t = 3 – 2i
   Với t = 3+ 2i thì z + 3 – i = 3 + 2i hay z = 3i
   Với t = 3- 2i thì z + 3 – i = 3 -2i hay z = – i

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Tìm nghịch đảo của số phức z, biết z thỏa mãn | z – 2i| =|z¯ + 2 + 4i| và z-iz¯+ i  là số thuần ảo.
   
   

   Câu hỏi:
   

   Tìm nghịch đảo của số phức z, biết z thỏa mãn | z – 2i| =|$\overline{z}$ + 2 + 4i| và $\frac{z–i}{\overline{z}+ i }$ là số thuần ảo.

   

   

   

   Đáp án chính xác

   

   Trả lời:

   Chọn C.
   Giả sử z = a+ bi thì  khi và chỉ khi a = b – 4  (1)
   Với a ≠ 0  hoặc b ≠ 1, ta có:
   
   Vì  là số thuần ảo nên a² – ( b – 1) ² = 0 khi và chỉ khi a = b – 1 hoặc a = 1 – b
   Kết hợp (1)  ta có a = -3/2 và b = 5/2.
   Nên số phức đó là
   Vậy $\frac{1}{z}=–\frac{3}{17}–\frac{5}{17}i$.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====