Trong không gian Oxyz, cho hình bình hành ABCD với A(0;1;-2), B(3;-2;1), D(1;4;2). Tọa độ của điểm C là:

Câu hỏi:

Trong không gian Oxyz, cho hình bình hành ABCD với A(0;1;-2), B(3;-2;1), D(1;4;2). Tọa độ của điểm C là:

A. (4;1;5)

Đáp án chính xác

B. (4;3;1)

C. (4;2;3)

D. (4;1;1)

Trả lời:

Đáp án A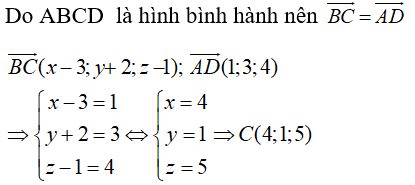

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Trong không gian Oxyz, cho hai vectơ a→ = (1; -2; 2), b→ = (-2; m – 3; m). Với những giá trị nào của m thì hai vectơ a→ và b→ có độ dài bằng nhau?
   
   

   Câu hỏi:
   

   Trong không gian Oxyz, cho hai vectơ $\overrightarrow{\mathrm{a}}$ = (1; -2; 2), $\overrightarrow{\mathrm{b}}$ = (-2; m – 3; m). Với những giá trị nào của m thì hai vectơ $\overrightarrow{\mathrm{a}}$ và $\overrightarrow{\mathrm{b}}$ có độ dài bằng nhau?

   A. m = 1 hoặc m = 2

   Đáp án chính xác

   B. m = 1

   C. m = 2

   D. Không có m

   Trả lời:

   Đáp án A

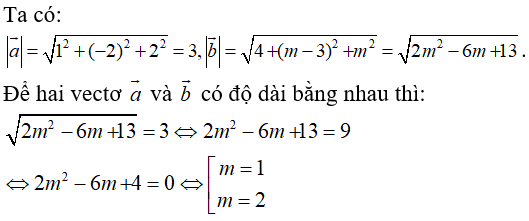
   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Trong không gian Oxyz, cho điểm G(1;2;3) là trọng tâm của tam giác ABC trong đó A thuộc trục Ox, B thuộc trục Oy, C thuộc trục Oz. Tọa độ các điểm A, B, C là:
   
   

   Câu hỏi:
   

   Trong không gian Oxyz, cho điểm G(1;2;3) là trọng tâm của tam giác ABC trong đó A thuộc trục Ox, B thuộc trục Oy, C thuộc trục Oz. Tọa độ các điểm A, B, C là:

   A. A(1; 0; 0), B(0; 2; 0), C(0; 0; 3)

   B. A(3; 0; 0), B(0; 6; 0), C(0; 0; 9)

   Đáp án chính xác

   C. A(-3; 0; 0), B(0; -6; 0), C(0; 0; -9)

   D. A(6; 0; 0), B(0; 3; 0), C(0; 0; 9)

   Trả lời:

   Đáp án BDo A thuộc trục Ox, B thuộc trục Oy, C thuộc trục Oz nên A(a; 0; 0); B(0; b; 0) và C(0; 0; c).Mà điểm G(1;2;3) là trọng tâm của tam giác ABC nên:

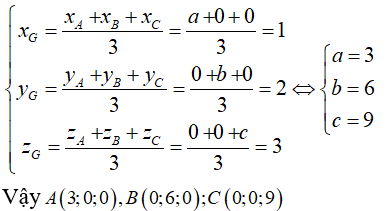
   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Trong không gian Oxyz, ba điểm nào dưới đây lập thành ba đỉnh của một tam giác?
   
   

   Câu hỏi:
   

   Trong không gian Oxyz, ba điểm nào dưới đây lập thành ba đỉnh của một tam giác?

   A. A(1; 2; 3), B(5; -4; -1), C(3; -1; 1)

   B. A(1; 2; 3), B(5; -4; -1), C(6; -2; 2)

   Đáp án chính xác

   C. A(1; 2; 3), B(5; -4; -1), C(9; -10; -5)

   D. A(1; 2; 3), B(5; -4; -1), C(-3; 8; 7)

   Trả lời:

   Đáp án BĐể ba điểm A, B,C lập thành ba đỉnh của 1 tam giác khi và chỉ khi ba điểm A, B,C không thẳng hàng hay hai vecto $\overrightarrow{\mathrm{AB}}$; $\overrightarrow{\mathrm{AC}}$ không cùng phươngXét phương án B ta có:$\overrightarrow{\mathrm{AB}}$ = (4; -6; -4); $\overrightarrow{\mathrm{AC}}$ = (5; -4; -1)Suy ra hai vecto này không cùng phương hay 3 điểm A, B, C không thằng hàng.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Cho hai vectơ a→, b→ thay đổi nhưng luôn thỏa mãn  Giá trị lớn nhất của
   
   

   Câu hỏi:
   

   Cho hai vectơ $\overrightarrow{\mathrm{a}}, \overrightarrow{\mathrm{b}}$ thay đổi nhưng luôn thỏa mãn 
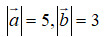
   Giá trị lớn nhất của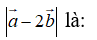

   A. 11

   Đáp án chính xác

   B. -1

   C. 1

   D. $\sqrt{61}$

   Trả lời:

   Đáp án ASử dụng bất đẳng thức vectơ: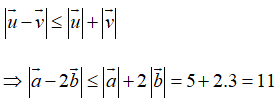Dấu bằng xảy ra khi và chỉ khi hai vectơ này ngược hướng. Suy ra đáp án A.Hai đáp án B và C xuất phát từ sai lầm

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Trong không gian cho hai điểm A(x; y; z), B(m, n, p) thay đổi nhưng luôn thỏa mãn các điều kiện x2 + y2 + z2 = 4, m2 + n2 + p2  = 9. Vectơ AB→ có độ dài nhỏ nhất là:
   
   

   Câu hỏi:
   

   Trong không gian cho hai điểm A(x; y; z), B(m, n, p) thay đổi nhưng luôn thỏa mãn các điều kiện ${\mathrm{x}}^2 + {\mathrm{y}}^{2 }+ {\mathrm{z}}^2$ = 4,${\mathrm{m}}^2 + {\mathrm{n}}^2 + {\mathrm{p}}^2$  = 9. Vectơ $\overrightarrow{\mathrm{AB}}$ có độ dài nhỏ nhất là:

   A. 5

   B. 1

   Đáp án chính xác

   C. 13

   D. Không tồn tại

   Trả lời:

   Đáp án B
   Từ giả thiết suy ra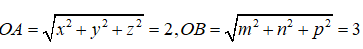
   Do đó AB ≥ |OA – OB| = 1. Dấu bằng xảy ra khi O nằm ngoài đoạn AB. Suy ra đáp án đúng là B.
   Hai đáp án A, D sai do nhầm OA = ${\mathrm{x}}^2 + {\mathrm{y}}^{2 }+ {\mathrm{z}}^2$ = 4; OB = ${\mathrm{m}}^2 + {\mathrm{n}}^2 + {\mathrm{p}}^2$ = 9
   Đáp án C sai do nhầm với câu hỏi vectơ $\overrightarrow{AB}$ có độ dài lớn nhất
    

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====