Câu hỏi:
Cho hình lập phương , gọi I là trung điểm . Mặt phẳng chia khối lập phương thành 2 phần. Tính tỉ số thể tích phần bé chia phần lớn.
A.
Đáp án chính xác
B.
C.
D.
Trả lời:
Phương pháp giải:
– Xác định thiết diện của thiết của hình lập phương khi cắt bởi .
– Phân chia khối đa diện chứa đỉnh C thành tổng hiểu của các khối đa diện có thể tính thể tích dễ dàng, so sánh thể tích của nó với thể tích khối lập phương. Từ đó suy ra tỉ số thể tích phần bé chia phần lớn.
Giải chi tiết:
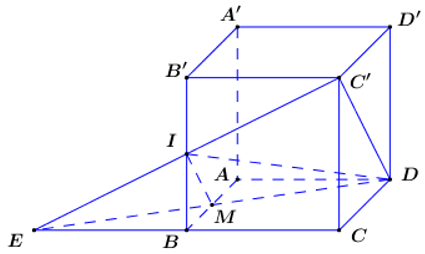
Trong gọi , trong gọi .
Khi đó cắt hình lập phương theo thiết diện là tứ giác .
Gọi là thể tích phần khối đa diện bị chia bởi chứa điểm C, khi đó ta có .
Ta có: .
Áp dụng định lí Ta-lét ta có: .
Khi đó ta có: .
.
Áp dụng định lí Ta-lét ta có: .
Khi đó ta có .
Vậy tỉ số thể tích phần bé chia phần lớn là .
Đáp án A
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Tập xác định D của hàm số y=2020sinx là:
Câu hỏi:
Tập xác định của hàm số là:
A.
B.
C.
D.
Đáp án chính xác
Trả lời:
Phương pháp giải:
– Hàm số xác định với mọi .
– Hàm phân thức xác định khi mẫu thức khác 0.
Giải chi tiết:
Hàm số xác định khi và chỉ khi .
Vậy TXĐ của hàm số là .
Đáp án D====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Tìm hệ số của x12 trong khai triển (2x−x2)10 .
Câu hỏi:
Tìm hệ số của trong khai triển .
A.
B.
Đáp án chính xác
C.
D.
Trả lời:
Phương pháp giải:
– Khai triển nhị thức Niu-tơn .
– Tìm hệ số của số hạng chứa trong khai triển.
Giải chi tiết:
Ta có: .
Khi đó để tìm hệ số của số hạng chứa , ta cho .
Vậy hệ số của số hạng chứa trong khai triển trên là .
Đáp án B====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AD=a,AB=2a . Cạnh bên SA vuông góc với đáy. Gọi M,N lần lượt là trung điểm của SB và SD. Tính khoảng cách d từ S đến mặt phẳng (AMN) .
Câu hỏi:
Cho hình chóp có đáy là hình chữ nhật với . Cạnh bên SA vuông góc với đáy. Gọi M,N lần lượt là trung điểm của SB và SD. Tính khoảng cách d từ S đến mặt phẳng .
A.
Đáp án chính xác
B.
C.
D.
Trả lời:
Phương pháp giải:
– Tính thể tích chóp , sử dụng tỉ lệ thể tích Simpson tính thể tích khối chóp .
– Sử dụng công thức
với p là nửa chu vi .
Giải chi tiết:
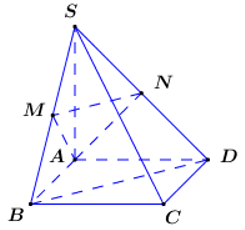
Áp dụng định lí Pytago trong các tam giác vuông ta có:
Khi đó ta có (đường trung tuyến trong tam giác vuông).
Ta có: MN là đường trung bình của nên .
Gọi p là nửa chu vi tam giác ta có: .
⇒ Diện tích tam giác là
Ta có: .
Mà .
Lại có , do đó .
Vậy
Đáp án A.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Tìm giá trị lớn nhất của hàm số f(x)=x3−3×2−4x+1 trên đoạn [1;3] .
Câu hỏi:
Tìm giá trị lớn nhất của hàm số trên đoạn .
A.
B.
C.
Đáp án chính xác
D.
Trả lời:
Phương pháp giải:
Sử dụng MTCT, chức năng MODE 7.
Giải chi tiết:
Sử dụng MODE 7, nhập , chọn Start = 1, End = 3, Step = 0,1.
Do cột :
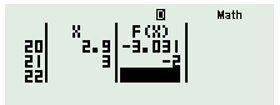
Vậy .
Đáp án C====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Nếu các số 5+m, 7+2m, 17+m theo thứ tự lập thành cấp số cộng thì m bằng bao nhiêu?
Câu hỏi:
Nếu các số , , theo thứ tự lập thành cấp số cộng thì m bằng bao nhiêu?
A.
B.
C.
Đáp án chính xác
D.
Trả lời:
Phương pháp giải:
Sử dụng tính chất của cấp số cộng: Nếu ba số lần lượt lập thành một cấp số cộng thì .
Giải chi tiết:
Vì theo thứ tự lập thành cấp số cộng nên ta có:
Đáp án C====== **** mời các bạn xem câu tiếp bên dưới **** =====