Cho hàm số trùng phương y=ax4+bx2+c có đồ thị như hình vẽ. Hỏi đồ thị hàm số y=x4+2×3−4×2−8x[f(x)]2+2f(x)−3 có tổng cộng bao nhiêu tiệm cận đứng?

Câu hỏi:

Cho hàm số trùng phương $y=a{x}^4+b{x}^2+c$ có đồ thị như hình vẽ. Hỏi đồ thị hàm số $y=\frac{x^4+2x^3-4x^2-8x}{{\left[f\left(x\right)\right]}^2+2f\left(x\right)-3}$ có tổng cộng bao nhiêu tiệm cận đứng?

A.2

B.3

C.5

D.4

Đáp án chính xác

Trả lời:

 
Ta có ${\left[f\left(x\right)\right]}^2+2f\left(x\right)-3=0\iff [\begin{array}{l}f\left(x\right)=1\\ f\left(x\right)=-3\end{array}.$
Phương trình $f\left(x\right)=1$ có nghiệm $x=\mathrm{0,}x=m,x=n$ trong đó $x=0$ là nghiệm kép.
Do đó $f\left(x\right)-1=a{x}^2(x-m)(x-n).$
Phương trình $f\left(x\right)=-3$ có 2 nghiệm kép $x=\mathrm{2,}x=-2.$
Do đó $f\left(x\right)+3=a{(x-2)}^2+{(x+2)}^2.$
Vì vậy ${\left[f\left(x\right)\right]}^2+2f\left(x\right)-3=a^2{x}^2(x-m)(x-n){(x-2)}^2{(x+2)}^2.$
Khi đó ta được hàm số $y=\frac{x(x-2){(x+2)}^2}{a^2{x}^2(x-m)(x-n){(x-2)}^2{(x+2)}^2}.$
$\underset{x\to 0^{+}}{\lim }y=+\infty$ nên đương thẳng  là tiệm cận đứng.
$\underset{x\to m^{+}}{\lim }y=+\infty$ nên đường thẳng $x=0$ là tiệm cận đứng.
$\underset{x\to 2^{+}}{\lim }y=-\infty$ nên đường thẳng $x=2$ là tiệm cận đứng.
$\underset{x\to -2}{\lim }y=\frac{-4}{a^{2}8(-2-m)(-2-n)}$ nên đường thẳng $x=-2$ không là tiệm cận đứng.
$\underset{x\to n^{+}}{\lim }y=+\infty$ nên đường thẳng $x=2$  là tiệm cận đứng.
Vậy đồ thị hàm số đã cho có 4 tiệm cận đứng.
Đáp án D

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Cho hình chóp S.ABC có SA⊥(ABC) và H là hình chiếu vuông góc của S lên BC. Khi đó BC vuông góc với đường thẳng nào sau đây?
   
   

   Câu hỏi:
   

   Cho hình chóp S.ABC có $SA\perp \left(ABC\right)$ và H là hình chiếu vuông góc của S lên BC. Khi đó BC vuông góc với đường thẳng nào sau đây?

   A.SC

   B.AC

   C.AB

   D.AH

   Đáp án chính xác

   Trả lời:

   

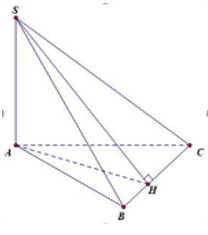
   Ta có:$\begin{array}{l}BC\perp SA\\ BC\perp SH\end{array}\}\Rightarrow BC\perp AH$
   Vậy $BC\perp AH.$
   Đáp án D

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Tính thể tích khối hộp chữ nhật có ba kích thước là 2, 3, 4.
   
   

   Câu hỏi:
   

   Tính thể tích khối hộp chữ nhật có ba kích thước là 2, 3, 4.

   A.24

   B.20

   Đáp án chính xác

   C.9

   D.12

   Trả lời:

   Áp dụng công thức tính thể tích khối hộp chữ nhật ta có:
   $V=abc=\mathrm{2.3.4}=24$ (đvtt)
   Đáp án B

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Đường tiệm cận ngang của đồ thị hàm số y=3xx+4 có phương trình là
   
   

   Câu hỏi:
   

   Đường tiệm cận ngang của đồ thị hàm số $y=\frac{3x}{x+4}$ có phương trình là

   A.$x=3.$

   B.$y=-4.$

   C.$y=3.$

   Đáp án chính xác

   D.$x=-4.$

   Trả lời:

   $\underset{x\to +\infty }{\lim }y=\underset{x\to -\infty }{\lim }y=3$nên đồ thị hàm số có tiệm cận ngang là $y=3.$
   Đáp án C

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Cho tập A={0;1;2;3;4;5;6}, có bao nhiêu tập con gồm 3 phần tử của tập hợp A?
   
   

   Câu hỏi:
   

   Cho tập $A=\{0;1;2;3;4;5;6\},$ có bao nhiêu tập con gồm 3 phần tử của tập hợp A?

   A.$P_3.$

   B.$C_7^3.$

   Đáp án chính xác

   C.$A_7^3.$

   D.$P_3.$

   Trả lời:

   Số tập con có 3 phần tử là: $C_7^3.$
   Đáp án B

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M,N lần lượt là trung điểm =AD và BC. Giao tuyến của hai mặt phẳng (SMN) và (SAC) là
   
   

   Câu hỏi:
   

   Cho hình chóp $S.ABCD$ có đáy ABCD là hình bình hành. Gọi M,N lần lượt là trung điểm =AD và BC. Giao tuyến của hai mặt phẳng $\left(SMN\right)$ và $\left(SAC\right)$ là

   A.SC(G là trung điểm AB)

   B.SD

   C.SF(F là trung điểm CD)

   D.$SO(O$ là tâm hình bình hành $ABCD).$

   Đáp án chính xác

   Trả lời:

   

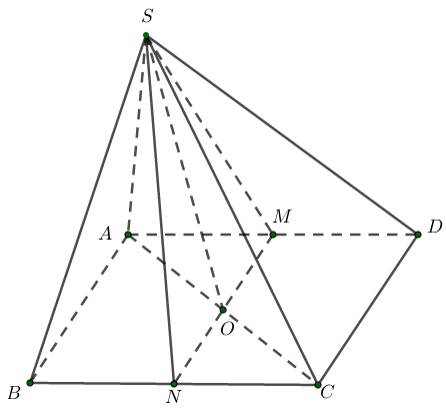
   Xét hai mặt phẳng $\left(SMN\right)$ và $\left(SAC\right)$ ta có:
         $\{\begin{array}{l}S\in \left(SMN\right)\\ S\in \left(SAC\right)\end{array}\left(1\right)$                   $\{\begin{array}{l}O\in AC\subset \left(SAC\right)\\ O\in MN\subset \left(SMN\right)\end{array}\left(2\right)$
   Từ (1) và (2) suy ra $\left(SMN\right)\cap \left(SAC\right)=SO.$
   Đáp án D

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====