Câu hỏi:
Gọi \(m\) và \(M\) lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số \(y = \frac{1}{2}x – \sqrt {x + 2} \) trên đoạn \(\left[ { – 1;34} \right].\) Tổng \(S = 3m + M\) bằng
A.\(S = \frac{{13}}{2}.\)
Đáp án chính xác
B.\(S = \frac{{25}}{2}.\)
C.\(S = \frac{{63}}{2}.\)
D.\(S = \frac{{11}}{2}.\)
Trả lời:
\(y’ = \frac{1}{2} – \frac{1}{{2\sqrt {x + 2} }} = \frac{{\sqrt {x + 2} – 1}}{{2\sqrt {x + 2} }}\)
\(y’ = 0 \Leftrightarrow \sqrt {x + 1} = 1 \Leftrightarrow x = – 1\)
\(f\left( { – 1} \right) = – \frac{3}{2};f\left( {34} \right) = 11.\)
\(m = – \frac{3}{2};M = 11.S = 3\left( { – \frac{3}{2}} \right) + 11 = \frac{{ – 9}}{2} + 11 = \frac{{13}}{2}.\)
Đáp án A.
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Trong các hàm số sau hàm số nào nghịch biến trên tập số thực
Câu hỏi:
Trong các hàm số sau hàm số nào nghịch biến trên tập số thực
A.\(y = {x^2} – 5x + 6.\)
B.\(y = – {x^3} + 2{x^2} – 10x + 4.\)
Đáp án chính xác
C.\(y = x + 5.\)
D. \(y = \frac{{x + 10}}{{x – 1}}.\)
Trả lời:
Vì hàm số bậc 2 và hàm phân thức bậc nhất nên không đơn điệu trên tập xác định nên loại đi hai đáp án A và D.Hàm số bậc nhất \(y = x + 5\) có hệ số \(a = 1 >0\) nên hàm số luôn đồng biến trên \(\mathbb{R}\) nên loại đáp án C. Vậy chọn đáp án B.
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho hàm số \(f\left( x \right)\) có bảng biến thiên:
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
Câu hỏi:
Cho hàm số \(f\left( x \right)\) có bảng biến thiên:
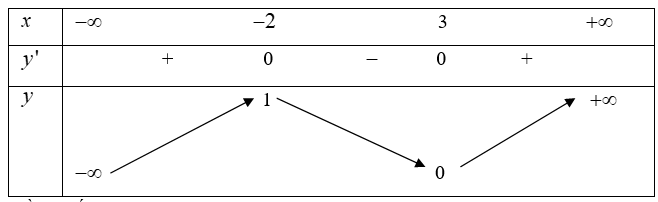
Hàm số đã cho đồng biến trên khoảng nào dưới đây?A.\(\left( { – \infty ;1} \right).\)
B.\(\left( {3;5} \right).\)
Đáp án chính xác
C.\(\left( { – 2;3} \right).\)
D. \(\left( {0; + \infty } \right).\)
Trả lời:
Dựa vào bảng biến thiên ta thấy hàm số \(f\left( x \right)\) đồng biến trên \(\left( {3; + \infty } \right)\) nên hàm số cũng đồng biến trên khoảng \(\left( {3;5} \right).\)
Đáp án B.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho hàm số bậc ba \(y = f\left( x \right)\) có đồ thị như hình vẽ.
Hàm số \(y = f\left( {\left| {x + 1} \right| – 1} \right)\) có bao nhiêu điểm cực trị?
Câu hỏi:
Cho hàm số bậc ba \(y = f\left( x \right)\) có đồ thị như hình vẽ.
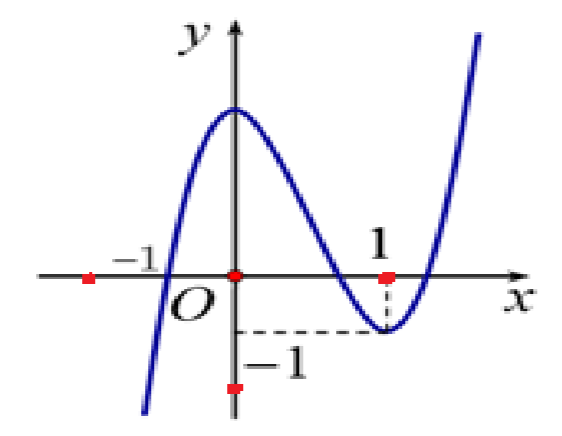
Hàm số \(y = f\left( {\left| {x + 1} \right| – 1} \right)\) có bao nhiêu điểm cực trị?A.5.
Đáp án chính xác
B.6.
C.7.
D. 8.
Trả lời:
Xét hàm số \(y = f\left( {\left| {x + 1} \right| – 1} \right)\)
Ta có: \(y’ = \frac{{x + 1}}{{\left| {x + 1} \right|}}f’\left( {\left| {x + 1} \right| – 1} \right)\)
Khi đó \(y’\) không xác định tại \(x = – 1\)
\(y’ = 0 \Leftrightarrow \left[ \begin{array}{l}\left| {x + 1} \right| – 1 = 0\\\left| {x + 1} \right| – 1 = 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = 0\\x = – 2\\x = – 3\end{array} \right.\)
Ta có bảng biến thiên:
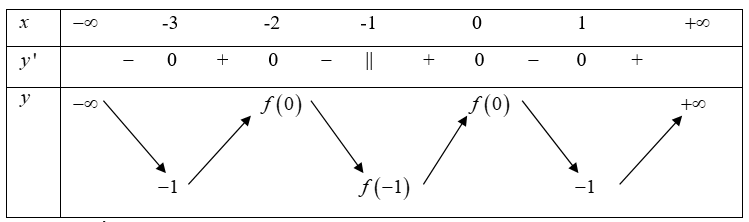
Dựa vào BBT hàm số có 5 cực trị nên chọn đáp án A.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho hình lăng trụ đứng \(ABC.A'B'C'\) có điểm \(O\) và \(G\) lần lượt là tâm của mặt bên \(ABB'A'\) và trọng tâm của \(\Delta ABC.\) Biết \({V_{ABC.A'B'C'}} = 270c{m^3}.\) Thể tích của khối chóp \(AOGB\) bằng
Câu hỏi:
Cho hình lăng trụ đứng \(ABC.A’B’C’\) có điểm \(O\) và \(G\) lần lượt là tâm của mặt bên \(ABB’A’\) và trọng tâm của \(\Delta ABC.\) Biết \({V_{ABC.A’B’C’}} = 270c{m^3}.\) Thể tích của khối chóp \(AOGB\) bằng
A.\(25c{m^3}.\)
B.\(30c{m^3}.\)
C.\(15c{m^3}.\)
Đáp án chính xác
D. \(45c{m^3}.\)
Trả lời:
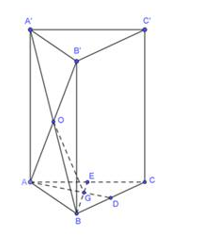
Ta có:
\(d\left( {O,\left( {ABC} \right)} \right) = \frac{1}{2}AA’\)
\({S_{\Delta AOB}} = \frac{1}{2}d\left( {G;AB} \right).AB\) mà \(d\left( {G;AB} \right) = \frac{1}{3}d\left( {C;AB} \right).\) Khi đó \({S_{\Delta AGB}} = \frac{1}{3}{S_{\Delta ABC}}\)
Vậy: \({V_{OAGB}} = \frac{1}{{18}}{V_{ABC.A’B’C’}} = \frac{1}{{18}}.270 = 15c{m^3}\) nên chọn đáp án C.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Có bao nhiêu cách sắp xếp 5 học sinh thành một hàng dọc?
Câu hỏi:
Có bao nhiêu cách sắp xếp 5 học sinh thành một hàng dọc?
A.\({5^5}.\)
B.\(5!.\)
Đáp án chính xác
C.\(4!.\)
D. 5.
Trả lời:
Đáp án B.
====== **** mời các bạn xem câu tiếp bên dưới **** =====