Câu hỏi:
Một công ty cần xây dựng một kho chứa hàng dạng hình hộp chữ nhật (bằng vật liệu gạch và xi măng) có thể tích \(2000{m^3},\) đáy là hình chữ nhật có chiều dài bằng hai lần chiều rộng. Người ta cần tính toán sao cho chi phí xây dựng là thấp nhất, biết giá xây dựng là \(750.000\) đ/m2. Khi đó chi phí thấp nhất gần với số nào dưới đây?
A. 742.935.831.
B. 742.963.631.
C. 742.933.631.
Đáp án chính xác
D. 742.833.631.
Trả lời:
Gọi chiều rộng của đáy hình chữ nhật là \(x\left( m \right)\) thì chiều dài của đáy là \(2x\left( m \right)\) với \(x >0.\)
Chiều cao của kho chứa là \(h\left( m \right)\) với \(h >0.\)
Theo giả thiết, ta có \(x.2x.h = 2000 \Leftrightarrow h = \frac{{1000}}{{{x^2}}}.\)
Diện tích toàn phần của kho chứa là \(S = 2x.2x + 2.2x.h + 2.x.h = 4{x^2} + \frac{{6000}}{x}.\)
Để chi phí xây dựng thấp nhất thì diện tích toàn phần của kho chứa phải nhỏ nhất.
Ta có \(S’ = 8x – \frac{{6000}}{{{x^2}}} = \frac{{8{x^3} – 6000}}{{{x^2}}}.\)
\(S’ = 0 \Leftrightarrow 8{x^3} – 6000 = 0 \Leftrightarrow x = 5\sqrt[3]{6}.\)
Bảng biến thiên
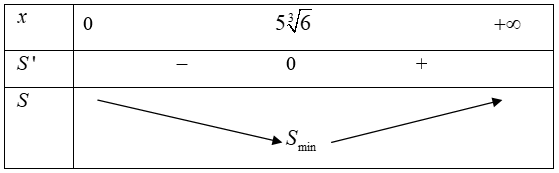
Vậy \({S_{\min }} = S\left( {5\sqrt[3]{6}} \right) \Rightarrow \) chi phí thấp nhất là \(\left[ {4.{{\left( {5\sqrt[3]{6}} \right)}^2} + \frac{{6000}}{{5\sqrt[3]{6}}}} \right].750000 \approx 742933631.\)
Đáp án C.
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Trong các hàm số sau hàm số nào nghịch biến trên tập số thực
Câu hỏi:
Trong các hàm số sau hàm số nào nghịch biến trên tập số thực
A.\(y = {x^2} – 5x + 6.\)
B.\(y = – {x^3} + 2{x^2} – 10x + 4.\)
Đáp án chính xác
C.\(y = x + 5.\)
D. \(y = \frac{{x + 10}}{{x – 1}}.\)
Trả lời:
Vì hàm số bậc 2 và hàm phân thức bậc nhất nên không đơn điệu trên tập xác định nên loại đi hai đáp án A và D.Hàm số bậc nhất \(y = x + 5\) có hệ số \(a = 1 >0\) nên hàm số luôn đồng biến trên \(\mathbb{R}\) nên loại đáp án C. Vậy chọn đáp án B.
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho hàm số \(f\left( x \right)\) có bảng biến thiên:
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
Câu hỏi:
Cho hàm số \(f\left( x \right)\) có bảng biến thiên:
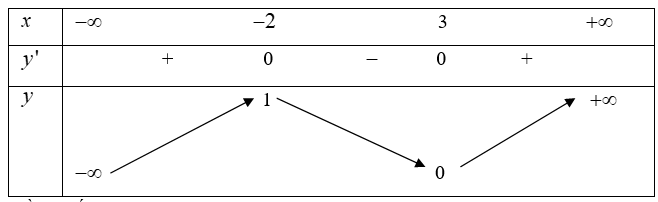
Hàm số đã cho đồng biến trên khoảng nào dưới đây?A.\(\left( { – \infty ;1} \right).\)
B.\(\left( {3;5} \right).\)
Đáp án chính xác
C.\(\left( { – 2;3} \right).\)
D. \(\left( {0; + \infty } \right).\)
Trả lời:
Dựa vào bảng biến thiên ta thấy hàm số \(f\left( x \right)\) đồng biến trên \(\left( {3; + \infty } \right)\) nên hàm số cũng đồng biến trên khoảng \(\left( {3;5} \right).\)
Đáp án B.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho hàm số bậc ba \(y = f\left( x \right)\) có đồ thị như hình vẽ.
Hàm số \(y = f\left( {\left| {x + 1} \right| – 1} \right)\) có bao nhiêu điểm cực trị?
Câu hỏi:
Cho hàm số bậc ba \(y = f\left( x \right)\) có đồ thị như hình vẽ.
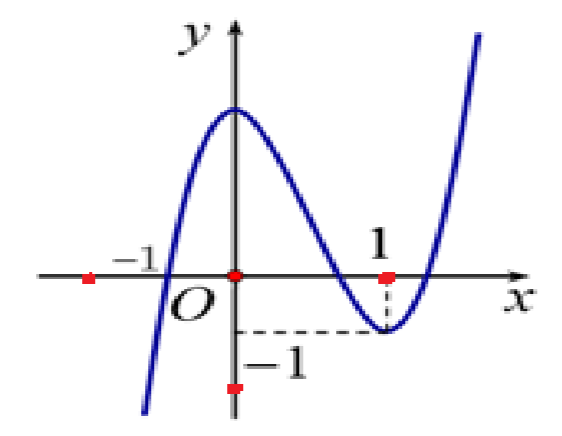
Hàm số \(y = f\left( {\left| {x + 1} \right| – 1} \right)\) có bao nhiêu điểm cực trị?A.5.
Đáp án chính xác
B.6.
C.7.
D. 8.
Trả lời:
Xét hàm số \(y = f\left( {\left| {x + 1} \right| – 1} \right)\)
Ta có: \(y’ = \frac{{x + 1}}{{\left| {x + 1} \right|}}f’\left( {\left| {x + 1} \right| – 1} \right)\)
Khi đó \(y’\) không xác định tại \(x = – 1\)
\(y’ = 0 \Leftrightarrow \left[ \begin{array}{l}\left| {x + 1} \right| – 1 = 0\\\left| {x + 1} \right| – 1 = 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = 0\\x = – 2\\x = – 3\end{array} \right.\)
Ta có bảng biến thiên:
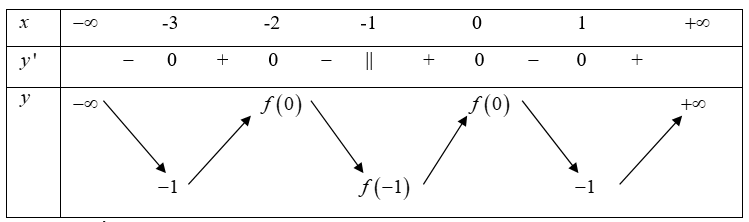
Dựa vào BBT hàm số có 5 cực trị nên chọn đáp án A.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho hình lăng trụ đứng \(ABC.A'B'C'\) có điểm \(O\) và \(G\) lần lượt là tâm của mặt bên \(ABB'A'\) và trọng tâm của \(\Delta ABC.\) Biết \({V_{ABC.A'B'C'}} = 270c{m^3}.\) Thể tích của khối chóp \(AOGB\) bằng
Câu hỏi:
Cho hình lăng trụ đứng \(ABC.A’B’C’\) có điểm \(O\) và \(G\) lần lượt là tâm của mặt bên \(ABB’A’\) và trọng tâm của \(\Delta ABC.\) Biết \({V_{ABC.A’B’C’}} = 270c{m^3}.\) Thể tích của khối chóp \(AOGB\) bằng
A.\(25c{m^3}.\)
B.\(30c{m^3}.\)
C.\(15c{m^3}.\)
Đáp án chính xác
D. \(45c{m^3}.\)
Trả lời:
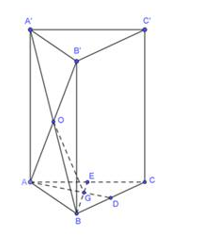
Ta có:
\(d\left( {O,\left( {ABC} \right)} \right) = \frac{1}{2}AA’\)
\({S_{\Delta AOB}} = \frac{1}{2}d\left( {G;AB} \right).AB\) mà \(d\left( {G;AB} \right) = \frac{1}{3}d\left( {C;AB} \right).\) Khi đó \({S_{\Delta AGB}} = \frac{1}{3}{S_{\Delta ABC}}\)
Vậy: \({V_{OAGB}} = \frac{1}{{18}}{V_{ABC.A’B’C’}} = \frac{1}{{18}}.270 = 15c{m^3}\) nên chọn đáp án C.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Có bao nhiêu cách sắp xếp 5 học sinh thành một hàng dọc?
Câu hỏi:
Có bao nhiêu cách sắp xếp 5 học sinh thành một hàng dọc?
A.\({5^5}.\)
B.\(5!.\)
Đáp án chính xác
C.\(4!.\)
D. 5.
Trả lời:
Đáp án B.
====== **** mời các bạn xem câu tiếp bên dưới **** =====