Câu hỏi:
Mệnh đề nào sau đây sai:
A.Hai khối hộp chữ nhật có diện tích toàn phần bằng nhau thì có thể tích bằng nhau.
Đáp án chính xác
B. Hai khối lăng trụ có diện tích đáy và chiều cao tương ứng bằng nhau thì có thể tích bằng nhau.
C.Hai khối lập phương có diện tích toàn phần bằng nhau thì có thể tích bằng nhau.
D.Hai khối chóp có diện tích đáy và chiều cao tương ứng bằng nhau thì có thể tích bằng nhau.
Trả lời:
Ta thấy các phương án B, C, D đúng, vậy phương án A sai
Đáp án A.
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Trong các phương trình dưới đây, phương trình nào có tập nghiệm là: \(x = \frac{\pi }{2} + k\pi ,k \in \mathbb{Z}.\)
Câu hỏi:
Trong các phương trình dưới đây, phương trình nào có tập nghiệm là: \(x = \frac{\pi }{2} + k\pi ,k \in \mathbb{Z}.\)
A.\(\sin x = 1\)
B.\(\cos x = 0\)
Đáp án chính xác
C.\(\sin x = 0\)
D. \(\cos x = 1\)
Trả lời:
Ta có: \(\sin x = 1 \Leftrightarrow x = \frac{\pi }{2} + k2\pi ,k \in \mathbb{Z}.\)
\(\cos x = 0 \Leftrightarrow x = \frac{\pi }{2} + k\pi ,k \in \mathbb{Z}.\)
\(\sin x = 0 \Leftrightarrow x = k\pi ,k \in \mathbb{Z}.\)
\(\cos x = 1 \Leftrightarrow x = k2\pi ,k \in \mathbb{Z}.\)
Đáp án B.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Đồ thị hàm số \(y = \frac{{x – 2}}{{x + 4}}\) cắt trục tung tại điểm có tung độ bằng
Câu hỏi:
Đồ thị hàm số \(y = \frac{{x – 2}}{{x + 4}}\) cắt trục tung tại điểm có tung độ bằng
A.0.
B.2.
C.\(\frac{1}{2}.\)
D. \( – \frac{1}{2}.\)
Đáp án chính xác
Trả lời:
Giao điểm của đồ thị hàm số với trục tung. Cho \(x = 0 \Rightarrow y = \frac{{0 – 2}}{{0 + 4}} = \frac{{ – 1}}{2}.\)
Vậy đồ thị hàm số \(y = \frac{{x – 2}}{{x + 4}}\) cắt trục tung tại điểm có tung độ bằng \(\frac{{ – 1}}{2}.\)
Đáp án D.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho hình chóp tứ giác có đáy là hình vuông cạnh \(a,\) khi cạnh đáy của hình chóp giảm đi 3 lần và vẫn giữ nguyên chiều cao thì thể tích của khối chóp giảm đi mấy lần:
Câu hỏi:
Cho hình chóp tứ giác có đáy là hình vuông cạnh \(a,\) khi cạnh đáy của hình chóp giảm đi 3 lần và vẫn giữ nguyên chiều cao thì thể tích của khối chóp giảm đi mấy lần:
A.6.
B.9.
Đáp án chính xác
C.27.
D. 3.
Trả lời:
* Thể tích hình chóp tứ giác có đáy là hình vuông cạnh \(a,\) chiều cao \(h\) là: \({V_1} = \frac{1}{3}{a^2}.h\)
* Thể tích hình chóp tứ giác có đáy là hình vuông cạnh \(\frac{a}{3},\) chiều cao \(h\) là: \({V_2} = \frac{1}{3}\frac{{{a^2}}}{9}h.\)
* Tỷ số thể tích là: \(\frac{{{V_1}}}{{{V_2}}} = 9.\)
Đáp án B.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Chọn kết quả sai trong các kết quả dưới đây:
Câu hỏi:
Chọn kết quả sai trong các kết quả dưới đây:
A.\(\mathop {\lim }\limits_{x \to {x_0}} x = {x_0}\)
B.\(\mathop {\lim }\limits_{x \to – \infty } {x^5} = – \infty \)
C.\(\mathop {\lim }\limits_{x \to + \infty } \frac{2}{{{x^2}}} = + \infty \)
Đáp án chính xác
D. \(\mathop {\lim }\limits_{x \to {1^ + }} c = c\)
Trả lời:
Ta có:
\(\mathop {\lim }\limits_{x \to {x_0}} x = {x_0}\)
\(\mathop {\lim }\limits_{x \to – \infty } {x^5} = – \infty \)
\(\mathop {\lim }\limits_{x \to + \infty } \frac{2}{{{x^2}}} = 0\)
\(\mathop {\lim }\limits_{x \to {1^ + }} c = c.\)
Đáp án C.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Hàm số \(y = \sqrt {2x – {x^2}} \) nghịch biến trên khoảng:
Câu hỏi:
Hàm số \(y = \sqrt {2x – {x^2}} \) nghịch biến trên khoảng:
A.\(\left( {0;1} \right)\)
B.\(\left( {1; + \infty } \right)\)
C.\(\left( {0;2} \right)\)
D. \(\left( {1;2} \right)\)
Đáp án chính xác
Trả lời:
Tập xác định \(D = \left[ {0;2} \right].\)
Ta có \(y’ = \frac{{1 – x}}{{\sqrt {2x – {x^2}} }},\forall x \in \left( {0;2} \right).\)
\(y’ = 0 \Leftrightarrow x = 1.\)
Bảng biến thiên
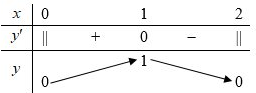
Dựa vào bảng biến thiên, ta thấy hàm số nghịch biến trên khoảng \(\left( {1;2} \right).\)
Đáp án D.====== **** mời các bạn xem câu tiếp bên dưới **** =====