Câu hỏi:
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ:
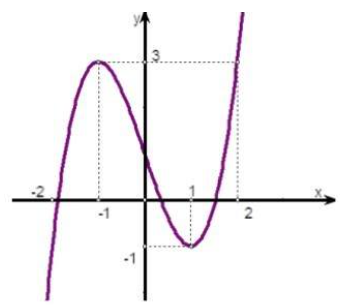
Gọi \(S\) là tập các giá trị nguyên của tham số \(m\) để phương trình \(f\left( {4\left| {\sin x} \right| + m} \right) – 3 = 0\) có đúng 12 nghiệm phân biệt thuộc nửa khoảng \(\left( {0;4\pi } \right].\) Tổng các phần tử của \(S\) bằng
A. \( – 3.\)
Đáp án chính xác
B. 1.
C. 3.
D. \( – 1.\)
Trả lời:
Đáp án A.
Phương trình đã cho tương đương với: \(f\left( {4\left| {\sin x} \right| + m} \right) = 3\left( * \right)\)
Từ đồ thị hàm số suy ra \(\left( * \right) \Leftrightarrow \left[ \begin{array}{l}4\left| {\sin x} \right| + m = – 1\\4\left| {\sin x} \right| + m = 2\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\left| {\sin x} \right| = – \frac{{m + 1}}{4}\left( 1 \right)\\\left| {\sin x} \right| = \frac{{2 – m}}{4}\left( 2 \right)\end{array} \right.\)
Điều kiện để phương trình (1) có nghiệm là: \(\left\{ \begin{array}{l} – \frac{{m + 1}}{4} \ge 0\\ – \frac{{m + 1}}{4} \le 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m + 1 \le 0\\m + 1 \ge – 4\end{array} \right. \Leftrightarrow – 5 \le m \le – 1.\)
Điều kiện để phương trình (2) có nghiệm là: \(\left\{ \begin{array}{l}\frac{{2 – m}}{4} \ge 0\\\frac{{2 – m}}{4} \le 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2 – m \ge 0\\2 – m \le 4\end{array} \right. \Leftrightarrow – 2 \le m \le 2.\)
Xét phương trình \(\left| {\sin x} \right| = \alpha \)
Nếu \(\alpha = 0\) thì \(\sin x = 0 \Leftrightarrow x = k\pi .\) Phương trình có 4 nghiệm thuộc khoảng \(\left( {0;4\pi } \right].\)
Nếu \(\alpha = 1\) thì \(\sin x = \pm 1 \Leftrightarrow x = \frac{\pi }{2} + k\pi .\) Phương trình có 4 nghiệm thuộc khoảng \(\left( {0;4\pi } \right].\)
Nếu \(0 < \alpha < 1\) thì \(\sin x = \pm \alpha .\) Phương trình có 8 nghiệm thuộc khoảng \(\left( {0;4\pi } \right].\)
Vậy nếu \(m < – 2\) thì phương trình \(\left( 2 \right)\) vô nghiệm, phương trình \(\left( 1 \right)\) chỉ có tối đa 8 nghiệm.
Nếu \(m >- 1\) thì phương trình \(\left( 1 \right)\) vô nghiệm, phương trình \(\left( 2 \right)\) chỉ có tối đa 8 nghiệm.
Vì \(m\) nguyên nên:
+) \(m = – 2\) Phương trình \(\left( 1 \right)\) có 8 nghiệm, phương trình \(\left( 2 \right)\) có 4 nghiệm (thỏa mãn).
+) \(m = – 1\) Phương trình \(\left( 2 \right)\) có 8 nghiệm, phương trình \(\left( 1 \right)\) có 4 nghiệm (thỏa mãn).
Vậy \(S = \left\{ { – 2; – 1} \right\}.\)
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Phương trình tiệm cận ngang của đồ thị hàm số \(y = \frac{{4 – 3x}}{{4x + 5}}\) là
Câu hỏi:
Phương trình tiệm cận ngang của đồ thị hàm số \(y = \frac{{4 – 3x}}{{4x + 5}}\) là
A.\(y = \frac{3}{4}.\)
B.\(y = – \frac{3}{4}.\)
Đáp án chính xác
C.\(x = \frac{3}{4}.\)
D. \(x = – \frac{5}{4}.\)
Trả lời:
Đáp án B
Vì \(\mathop {\lim }\limits_{x \to – \infty } \frac{{4 – 3x}}{{4x + 5}} = – \frac{3}{4}\) (hoặc \(\mathop {\lim }\limits_{x \to + \infty } \frac{{4 – 3x}}{{4x + 5}} = – \frac{3}{4}\)) nên đường thẳng \(y = – \frac{3}{4}\) là tiệm cận ngang của đồ thị hàm số đã cho.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho hình chóp \(S.ABCD\) có đáy là hình vuông cạnh \(a,SA\) vuông góc với mặt đáy và \(SA = a\sqrt 2 .\) Góc giữa đường thẳng \(SC\) và mặt phẳng \(\left( {ABCD} \right)\) bằng
Câu hỏi:
Cho hình chóp \(S.ABCD\) có đáy là hình vuông cạnh \(a,SA\) vuông góc với mặt đáy và \(SA = a\sqrt 2 .\) Góc giữa đường thẳng \(SC\) và mặt phẳng \(\left( {ABCD} \right)\) bằng
A.\({60^0}.\)
B.\({30^0}.\)
C.\({90^0}.\)
D. \({45^0}.\)
Đáp án chính xác
Trả lời:
Đáp án D
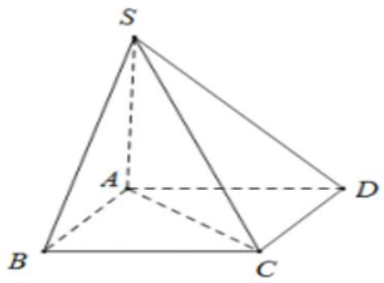
Ta có: \(SA \bot \left( {ABCD} \right) \supset AC \Rightarrow SA \bot AC \Rightarrow \left( {SC,\left( {ABCD} \right)} \right) = \widehat {SCA}.\)
Xét tam giác vuông \(SAC,\) ta có: \(\tan \widehat {SCA} = \frac{{SA}}{{AC}} = \frac{{a\sqrt 2 }}{{a\sqrt 2 }} = 1 \Rightarrow \widehat {SCA} = {45^0}.\)====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Hình bát diện đều có bao nhiêu cạnh?
Câu hỏi:
Hình bát diện đều có bao nhiêu cạnh?
A. 10.
B. 11.
C. 12.
Đáp án chính xác
D. 13.
Trả lời:
Đáp án C.
Hình bát diện đều có 12 cạnh.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho \(x,y,z\) là ba số dương lập thành cấp số nhân; còn \({\log _a}x;{\log _{\sqrt a }}y;{\log _{\sqrt[3]{a}}}z\) lập thành cấp số cộng. Tính giá trị của biểu thức \(Q = \frac{{2017x}}{y} + \frac{{2y}}{z} + \frac{z}{x}.\)
Câu hỏi:
Cho \(x,y,z\) là ba số dương lập thành cấp số nhân; còn \({\log _a}x;{\log _{\sqrt a }}y;{\log _{\sqrt[3]{a}}}z\) lập thành cấp số cộng. Tính giá trị của biểu thức \(Q = \frac{{2017x}}{y} + \frac{{2y}}{z} + \frac{z}{x}.\)
A. 2019.
B. 2021.
C. 2020.
Đáp án chính xác
D. 2018.
Trả lời:
Đáp án C.
Theo bài ra, \(x,y,z\) là ba số dương lập thành cấp số nhận và \({\log _a}x;{\log _{\sqrt a }}y;{\log _{\sqrt[3]{a}}}z\) lập thành cấp số cộng nên ta có: \(\left\{ \begin{array}{l}xz = {y^2}\\{\log _a}x + {\log _{\sqrt[3]{a}}}z = 2{\log _{\sqrt a }}y\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x.z = {y^2}\\{\log _a}x + 3{\log _a}z + 4{\log _a}y\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x.z = {y^2}\\{\log _a}x{z^3} = {\log _a}{y^4}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}xz = {y^2}\\x{z^3} = {y^4}\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}x.z = {y^2}\\{y^2}{z^2} = {y^4}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x.y = {y^2}\\z = y\end{array} \right. \Leftrightarrow x = y = z.\)
Do đó: \(Q = \frac{{2017x}}{y} + \frac{{2y}}{z} + \frac{z}{x} = \frac{{2017x}}{x} + \frac{{2x}}{x} + \frac{x}{x} = 2017 + 2 + 1 = 2020.\)====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Mặt cầu \(\left( S \right)\) có tâm \(I\) bán kính \(R\) có diện tích bằng
Câu hỏi:
Mặt cầu \(\left( S \right)\) có tâm \(I\) bán kính \(R\) có diện tích bằng
A. \(\frac{4}{3}\pi {R^2}.\)
B.\(4\pi {R^2}.\)
Đáp án chính xác
C.\(2\pi {R^2}.\)
D. \(\pi {R^2}.\)
Trả lời:
Đáp án B.
Diện tích mặt cầu \(\left( S \right)\) là \(S = 4\pi {R^2}.\)====== **** mời các bạn xem câu tiếp bên dưới **** =====