Cho các số phức z1, z2, z3 thỏa mãn |z1| = |z2| = 2|z3| = 2 và 3z1z2 = 4z3(z1 + z2). Gọi A, B, C lần lượt là các điểm biểu diễn của z1, z2, z3 trên mặt phẳng tọa độ. Diện tích tam giác ABC bằng

Câu hỏi:

Cho các số phức z₁, z₂, z₃ thỏa mãn |z₁| = |z₂| = 2|z₃| = 2 và 3z₁z₂ = 4z₃(z₁ + z₂). Gọi A, B, C lần lượt là các điểm biểu diễn của z₁, z₂, z₃ trên mặt phẳng tọa độ. Diện tích tam giác ABC bằng

A. $\frac{\sqrt{7}}{4};$

Đáp án chính xác

B.$\frac{3\sqrt{7}}{4};$

C. $\frac{\sqrt{7}}{2};$

D.$\frac{3\sqrt{7}}{2}.$

Trả lời:

Đáp án đúng là: A

Ta có 3z₁z₂ = 4z₃(z₁ + z₂) Þ |3z₁z₂| = |4z₃(z₁ + z₂)|
Û |3z₁z₂| = |4z₃(z₁ – (-z₂))|
Û |z₁ – (-z₂)| = 3
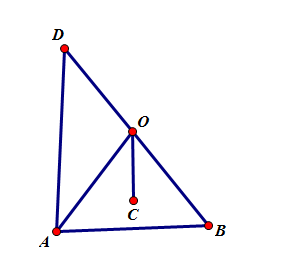
Lấy D đối xứng với B qua O, suy ra D biểu diễn (-z₂).
Ta có |z₁ – (-z₂)| = 3 Û AD = 3
DABD có trung tuyến  nên DABD vuông tại A
$\Rightarrow AB=\sqrt{B{D}^2-A{D}^2}=\sqrt{7}$

+) 3z₁z₂ = 4z₃(z₁ + z₂) Û z₁(3z₂ – 4z₃) = 4z₂z₃
Þ |z₁||3z₂ – 4z₃| = |4z₂z₃|
Þ |3z₂ – 4z₃| = 4
$\iff 9O{B}^2+16O{C}^2-24OB.OC.\cos \widehat{BOC}=16$
$\iff \cos \widehat{BOC}=\frac{3}{4}$

Áp dụng định lí cosin cho DBOC ta có:
$BC=\sqrt{O{B}^2+O{C}^2-2OB.OC.\cos \widehat{BOC}}=\sqrt{4+1-4.\frac{3}{4}}=\sqrt{2}$

Tương tự ta tính được $AC=\sqrt{2}$
Vậy $S_{ABC}=\frac{\sqrt{7}}{4}.$

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Cho hàm số f (x) = ex + 2x. Khẳng định nào dưới đây đúng?
   
   

   Câu hỏi:
   

   Cho hàm số f (x) = e^x + 2x. Khẳng định nào dưới đây đúng?

   A. $\int f\left(x\right)dx=e^x+2x^2+C;$ 

   B. $\int f\left(x\right)dx=e^x-x^2+C;$

   C.$\int f\left(x\right)dx=e^x+C;$

   D.$\int f\left(x\right)dx=e^x+x^2+C.$

   Đáp án chính xác

   Trả lời:

   Đáp án đúng là: D
   Ta có: $\int f\left(x\right)dx=\int \left(e^x+2x\right)dx=e^x+x^2+C.$

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Đạo hàm của hàm số y = x-3 là
   
   

   Câu hỏi:
   

   Đạo hàm của hàm số y = x^–3 là

   A. y’ = – x^–4;

   B. y’ = – 3x^–4;

   Đáp án chính xác

   C. $y‘=-\frac{1}{3}{x}^{-4};$

   D.$y‘=-\frac{1}{2}{x}^{-2}.$

   Trả lời:

   Đáp án đúng là: B
   Ta có: y’ = – 3x^{–3 – 1} = – 3x^–4.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Hàm số nào dưới đây có bảng biến thiên như sau?
   
   

   Câu hỏi:
   

   Hàm số nào dưới đây có bảng biến thiên như sau?
   

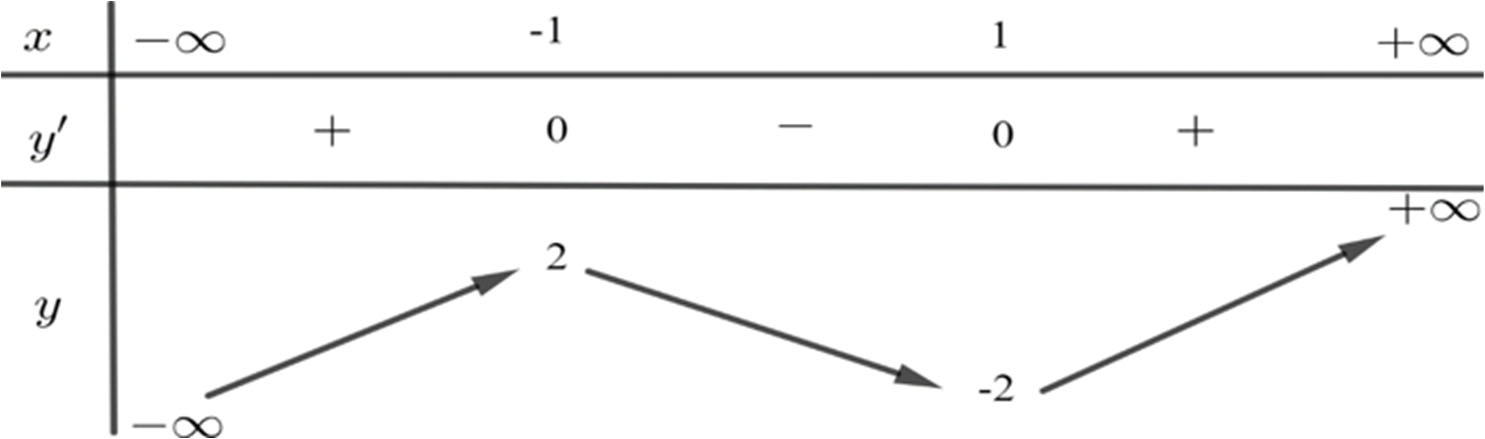
   A. y = -x³ + 3x;

   B. y = x³ – 3x;

   Đáp án chính xác

   C. y = -x⁴ + 2x²;

   D. y = x⁴ – 2x².

   Trả lời:

   Đáp án đúng là: B
   Từ BBT ta nhận thấy hàm số có hai điểm cực trị và đồng biến trên khoảng (1; +¥). Do đó hàm số là hàm đa thức bậc ba có hệ số a > 0.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Trong không gian Oxyz, phương trình mặt phẳng (Oyz) là
   
   

   Câu hỏi:
   

   Trong không gian Oxyz, phương trình mặt phẳng (Oyz) là

   A. x = 0;

   Đáp án chính xác

   B. x + y + z = 0;

   C. z = 0;

   D. y = 0.

   Trả lời:

   Đáp án đúng là: A
   Ta có một véc tơ pháp tuyến của mặt phẳng Oyz là: .
   Mặt phẳng đi qua gốc tọa độ O(0; 0; 0).
   Phương trình mặt phẳng (Oyz) là:
   1(x – 0) + 0(y – 0) + 0(z – 0) = 0 hay x = 0.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Tiệm cận ngang của đồ thị hàm số y=2x−12x+4 là đường thẳng có phương trình:
   
   

   Câu hỏi:
   

   Tiệm cận ngang của đồ thị hàm số $y=\frac{2x-1}{2x+4}$ là đường thẳng có phương trình:

   A. y = -2;

   B. x = -2;

   C. x = 1;

   D. y = 1.

   Đáp án chính xác

   Trả lời:

   Đáp án đúng là: D
   Ta có $\lim x\to +\infty =\lim x\to +\infty \frac{2x-1}{2x+4}=1$  và $\lim x\to -\infty =\lim x\to -\infty \frac{2x-1}{2x+4}=1$  .
   Vậy đồ thị hàm số có tiệm cận ngang là đường thẳng có phương trình y = 1.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====