Câu hỏi:
Anh Thưởng dự định sử dụng hết \(4{m^2}\) kính để làm bể cá có dạng hình hộp chữ nhật không nắp, chiều dài gấp đôi chiều rộng (các mối ghép không đáng kể). Bể cá có dung tích bằng bao nhiêu? (làm tròn đến chữ số phần trăm).
A.\(1,50{m^3}.\)
B.\(1,33{m^3}.\)
C.\(1,61{m^3}.\)
D. \(0,73{m^3}.\)
Đáp án chính xác
Trả lời:
Đáp án D.
Gọi \(x,2x,h\) lần lượt là ba kích thước của hồ. \(\left( {x \ge 0} \right)\)
Diện tích xung quanh và đáy hồ: \(S = 2{x^2} + 2.xh + 2.2xh = 2{x^2} + 6xh = 4\)
\( \Rightarrow h = \frac{{2 – {x^2}}}{{3x}}\left( {0 \le x \le \sqrt 2 } \right).\)
Thể tích hồ \(V = x.2x.h = \frac{{2x\left( {2 – {x^2}} \right)}}{3}\)
\(V’ = – 2{x^2} + \frac{4}{3}\)
\(V’ = 0 \Leftrightarrow \left[ \begin{array}{l}x = \frac{{\sqrt 6 }}{3}\\x = \frac{{ – \sqrt 6 }}{3}\left( l \right)\end{array} \right.\)
\(V\left( 0 \right) = 0\)
\(V\left( {\sqrt 2 } \right) = 0\)
\(V\left( {\frac{{\sqrt 6 }}{3}} \right) = \frac{{8\sqrt 6 }}{{27}} \approx 0.73\)
Vậy thể tích lớn nhất là câu D.
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Số đỉnh của một khối lăng trụ tam giác là
Câu hỏi:
Số đỉnh của một khối lăng trụ tam giác là
A.9.
B. 3.
C. 6.
Đáp án chính xác
D. 12.
Trả lời:
Đáp án C.
Khối lăng trụ tam giác có 6 đỉnh.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Đạo hàm của hàm số \(y = {x^4}\) là
Câu hỏi:
Đạo hàm của hàm số \(y = {x^4}\) là
A.\(y’ = 4{x^3}.\)
Đáp án chính xác
B.\(y’ = 0.\)
C.\(y’ = 4{x^2}.\)
D. \(y’ = 4x.\)
Trả lời:
Đáp án A.
Ta có: \(y’ = \left( {{x^4}} \right)’ = 4{x^3}.\)====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho hàm số \(y = f\left( x \right)\) xác định, liên tục trên \(\mathbb{R}\) và có bảng biến thiên sau:
Khẳng định nào sau đây là khẳng định đúng?
Câu hỏi:
Cho hàm số \(y = f\left( x \right)\) xác định, liên tục trên \(\mathbb{R}\) và có bảng biến thiên sau:
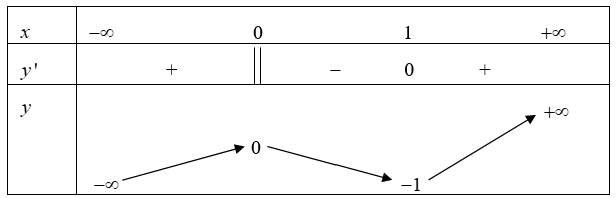
Khẳng định nào sau đây là khẳng định đúng?A. Hàm số có giá trị lớn nhất bằng 0 và giá trị nhỏ nhất bằng \( – 1.\)
B. Hàm số có đúng một cực trị.
C. Hàm số có giá trị cực tiểu bằng 1.
D. Hàm số đạt cực đại tại \(x = 0\) và đạt cực tiểu tại \(x = 1.\)
Đáp án chính xác
Trả lời:
Đáp án D.
Từ bảng biến thiên ta thấy, tính từ trái qua phải:
Dấu của \(y’\) đổi dấu từ (+) sang (-) khi qua \(x = 0,\) nên tại \(x = 0\) hàm số đạt cực đại.
Dấu của \(y’\) đổi dấu từ (-) sang (+) khi qua \(x = 1,\) nên tại \(x = 1\) hàm số đạt cực tiểu.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- \(\mathop {\lim }\limits_{x \to – 1} \left( {1 – x – {x^3}} \right)\) bằng
Câu hỏi:
\(\mathop {\lim }\limits_{x \to – 1} \left( {1 – x – {x^3}} \right)\) bằng
A.\( – 1.\)
B. 3.
Đáp án chính xác
C.\( – 3.\)
D. 1.
Trả lời:
Đáp án B.
Ta có: \(\mathop {\lim }\limits_{x \to – 1} \left( {1 – x – {x^3}} \right) = 1 – \left( { – 1} \right) – {\left( { – 1} \right)^3} = 3.\)====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho khối lăng trụ có diện tích đáy \(B = 6\) và chiều cao \(h = 3.\) Thể tích của khối lăng trụ đã cho bằng
Câu hỏi:
Cho khối lăng trụ có diện tích đáy \(B = 6\) và chiều cao \(h = 3.\) Thể tích của khối lăng trụ đã cho bằng
A. 18.
Đáp án chính xác
B. 54.
C. 36.
D. 2.
Trả lời:
Đáp án A.
Thể tích khối lăng trụ là \(V = Bh = 6.3 = 18.\)====== **** mời các bạn xem câu tiếp bên dưới **** =====