Câu hỏi:
Cho hình hộp chữ nhật \(ABCD.A’B’C’D’\) có \(AB = a;AD = 2a;AA’ = 2a.\) Tính diện tích của mặt cầu ngoại tiếp tứ diện \(ABB’C’?\)
A.\(9\pi {a^2}.\)
Đáp án chính xác
B.\(4\pi {a^2}.\)
C.\(12\pi {a^2}.\)
D. \(36\pi {a^2}.\)
Trả lời:
Đáp án A.
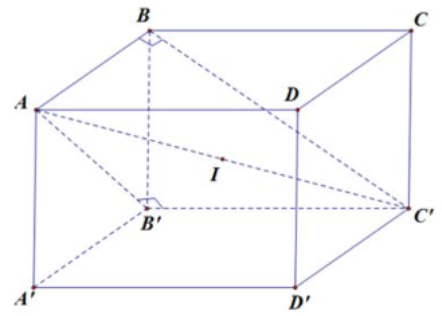
Ta có: \(AB \bot \left( {BCC’B’} \right) \Rightarrow AB \bot BC’ \Rightarrow \Delta ABC’\) vuông tại \(B.\)
Lại có: \(B’C’ \bot \left( {ABB’A’} \right) \Rightarrow B’C’ \bot AB’ \Rightarrow \Delta AB’C’\) vuông tại \(B’.\)
Gọi \(I\) là trung điểm của \(A’C \Rightarrow IA = IB = IB’ = IC’ = R.\) Mặt khác, \(I\) là tâm mặt cầu ngoại tiếp hình hộp chữ nhật nên \(R = \frac{1}{2}\sqrt {A{B^2} + A{D^2} + AA{‘^2}} = \frac{{3a}}{2}.\)
Vậy diện tích của mặt cầu ngoại tiếp tứ diện \(ABB’C’\) là: \(S = 4\pi {R^2} = 9\pi {a^2}.\)
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Trong các khẳng định dưới đây, khẳng định nào sai?
Câu hỏi:
Trong các khẳng định dưới đây, khẳng định nào sai?
A.\(\int\limits_{}^{} {kf\left( x \right)dx} = k\int\limits_{}^{} {f\left( x \right)dx} ,\left( {\forall k \ne 0} \right).\)
B.\(\int\limits_{}^{} {f’\left( x \right)dx} = f\left( x \right) + C.\)
C.\(\int\limits_{}^{} {\left[ {f\left( x \right) \pm g\left( x \right)} \right]dx} = \int\limits_{}^{} {f\left( x \right)dx} \pm \int\limits_{}^{} {g\left( x \right)dx} .\)
D. \(\int\limits_{}^{} {\left[ {f\left( x \right).g\left( x \right)} \right]dx} = \int\limits_{}^{} {f\left( x \right)dx} .\int\limits_{}^{} {g\left( x \right)dx} .\)
Đáp án chính xác
Trả lời:
Đáp án D.
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Tập nghiệm của bất phương trình \({3^x} \le 9\) là
Câu hỏi:
Tập nghiệm của bất phương trình \({3^x} \le 9\) là
A.\(\left( { – \infty ;2} \right).\)
B.\(\left( {2; + \infty } \right).\)
C.\(\left( { – \infty ; – 2} \right].\)
Đáp án chính xác
D. \(\left[ {2; + \infty } \right).\)
Trả lời:
Đáp án C.
Ta có \({3^x} \le 9 \Leftrightarrow {3^x} \le {3^2} \Leftrightarrow x \le 2.\)====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Gọi \(M\) và \(m\) lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y = {x^3} – 3x + 2\) trên đoạn \(\left[ {0;2} \right].\) Khi đó tổng \(M + m\) bằng
Câu hỏi:
Gọi \(M\) và \(m\) lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y = {x^3} – 3x + 2\) trên đoạn \(\left[ {0;2} \right].\) Khi đó tổng \(M + m\) bằng
A. 6.
B. 2.
C. 4.
Đáp án chính xác
D. 16.
Trả lời:
Đáp án C.
Ta có \(y’ = 3{x^2} – 3x,y’ = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0 \in \left[ {0;2} \right]\\x = 1 \in \left[ {0;2} \right]\end{array} \right.\)
\(y\left( 0 \right) = 2,y\left( 2 \right) = 4,y\left( 1 \right) = 0,\) vậy \(M = 4;m = 0\), do đó \(M + m = 4.\)====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ.
Hàm số \(y = f\left( x \right)\) đồng biến trên khoảng nào dưới đây?
Câu hỏi:
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ.
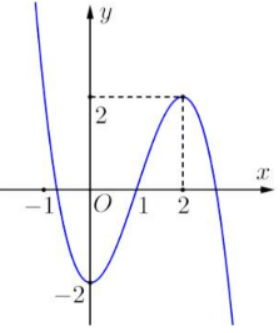
Hàm số \(y = f\left( x \right)\) đồng biến trên khoảng nào dưới đây?A.\(\left( {2; + \infty } \right).\)
B.\(\left( { – \infty ;0} \right).\)
C.\(\left( { – 2;2} \right).\)
D. \(\left( {0;2} \right).\)
Đáp án chính xác
Trả lời:
Đáp án D.
Dựa vào đồ thị, ta thấy hàm số đồng biến trên các khoảng \(\left( {0;2} \right).\)====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho khối cầu có bán kính \(R = 3\). Thể tích khối cầu đã cho bằng
Câu hỏi:
Cho khối cầu có bán kính \(R = 3\). Thể tích khối cầu đã cho bằng
A. \(36\pi .\)
Đáp án chính xác
B. \(4\pi .\)
C. \(12\pi .\)
D. \(108\pi .\)
Trả lời:
Đáp ánA.
Thể tích khối cầu đã cho bằng: \(V = \frac{4}{3}\pi {R^3} = \frac{4}{3}\pi {.3^3} = 36\pi .\)====== **** mời các bạn xem câu tiếp bên dưới **** =====