Xét tất cả số thực x, y sao cho 275−y2≥a6x−log3a3 với mọi số thực dương a. Giá trị nhỏ nhất của biểu thức P = x2 + y2 − 4x + 8y bằng

Câu hỏi:

Xét tất cả số thực x, y sao cho ${27}^{5-y^2}\ge a^{6x-{\log }_3{a}^3}$ với mọi số thực dương a. Giá trị nhỏ nhất của biểu thức P = x² + y² − 4x + 8y bằng

A. −15.

Đáp án chính xác

B. 25.

C. −5.

D. −20.

Trả lời:

Đáp án đúng là: A
Giả sử x, y thỏa với mọi số dương a
Ta có P = x² + y² − 4x + 8y  x² + y² − 4x + 8y − P = 0
Suy ra điểm M(x; y) thuộc đường tròn tâm I(2; −4) và bán kính $\sqrt{2^2+{(-4)}^2+P}$  =$\sqrt{20+P}$
(5 − y²).3 ≥ (6x − 3t)t
$\iff$−3t² + 6xt − 15 + 3y² ≤ 0 (với t = log₃a)
Theo đề bài ta có đúng với mọi số thực dương a nên −3t² + 6xt − 15 + 3y² ≤ 0 đúng với mọi t Î ℝ
Do đó $\left\{\begin{array}{c}-3<0\\ {\left(3x\right)}^2+3(-15+3y^2)\le 0\end{array}\right.$
9x² +9y² − 45 ≤ 0 x² + y² ≤ 5
Suy ra tập hợp các điểm M(x; y) là hình tròn tâm O(0; 0) và bán kinh R₂ =$\sqrt{5}$
Vậy để tồn tại cặp (x; y) thì đường tròn (I; R₁) và hình tròn (O; ) phải có điểm chung
Do đó IO ≤ R₁ +$\sqrt{5}$ $\iff$$\sqrt{2^2+{(-4)}^2}$ ≤$\sqrt{20+P}+\sqrt{5}$
$\iff$$\sqrt{5}$≤$\sqrt{20+P}$$\iff$ P ≥ −15
Vậy giá trị nhỏ nhất của P là −15.

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Hàm số nào dưới đây có bảng biển thiên như sau
   
   

   Câu hỏi:
   

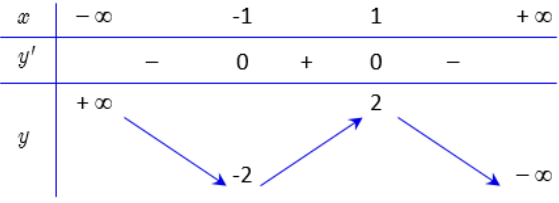
   Hàm số nào dưới đây có bảng biển thiên như sau
   

   A. y = x³ − 3x.

   Đáp án chính xác

   B. y = −x³ + 3x.

   C. y = x² − 2x.

   D. y = −x² + 2x.

   Trả lời:

   Đáp án đúng là: A
   Dựa vào bảng biến thiên ta nhận thấy:
   ∙ Đây là hàm y = ax³ + bx² + cx + d (a ≠ 0). Loại đáp án C và D.
   ∙ = −¥ Þ a < 0. Loại đáp án A.
   Do đó hàm số thỏa mã là y = −x³ +3x .

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Nếu ∫03f(x)dx = 6 thì ∫0313f(x)+2  dx bằng?
   
   

   Câu hỏi:
   

   Nếu $\underset{0}{\overset{3}{\int }}f\left(x\right)dx$ = 6 thì $\underset{0}{\overset{3}{\int }}\left[\frac{1}{3}f\left(x\right)+2\right]$  dx bằng?

   A. 8.

   Đáp án chính xác

   B. 5.

   C. 9.

   D. 6.

   Trả lời:

   Đáp án đúng là: A
   Ta có $\underset{0}{\overset{3}{\int }}\left[\frac{1}{3}f\left(x\right)+2\right]$ dx = $\frac{1}{3}$$\underset{0}{\overset{3}{\int }}f\left(x\right)dx$ +$\underset{0}{\overset{3}{\int }}2dx$ = $\frac{1}{3}$. 6 + ${\left.2x\right|}_0^3$ = 2 + 6 = 8 .

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Phần ảo của số phức z = (2 − i)(1 + i)
   
   

   Câu hỏi:
   

   Phần ảo của số phức z = (2 − i)(1 + i)

   A. 3.

   B. 1.

   Đáp án chính xác

   C. −1.

   D. −3.

   Trả lời:

   Đáp án đúng là: B
   Ta có z = (2 − i)(1 + i) = 3 + i.
   Vậy phần ảo của số phức z là 1.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Khẳng định nào dưới đây đúng ?
   
   

   Câu hỏi:
   

   Khẳng định nào dưới đây đúng ?

   A. = xe^x + C.

   B. = e^x+1  + C

   C. = −e^x+1 + C.

   D. = e^x + C.

   Đáp án chính xác

   Trả lời:

   Đáp án đúng là: D
   Ta có = e^x + C .

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Cho hàm số y = ax4 + bx2 + c có đồ thị là đường cong trong hình dưới. Giá trị cực tiểu của hàm số đã cho bằng
   
   

   Câu hỏi:
   

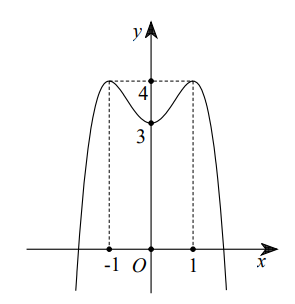
   Cho hàm số y = ax⁴ + bx² + c có đồ thị là đường cong trong hình dưới. Giá trị cực tiểu của hàm số đã cho bằng
   

   A. 1.

   B. 4.

   C. −1.

   D. 3.

   Đáp án chính xác

   Trả lời:

   Đáp án đúng là: D
   Dựa vào đồ thị hàm số ta thấy giá trị cực tiểu bằng 3 .

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====