Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB = a, AD = 2a. Tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với đáy. Góc giữa SC và mặt phẳng (ABCD) bằng 450. Gọi M là trung điểm SD, hãy tính theo a khoảng cách d từ M đến mặt phẳng (SAC). 

Câu hỏi:

Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB = a, AD = 2a. Tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với đáy. Góc giữa SC và mặt phẳng (ABCD) bằng ${45}^0.$ Gọi M là trung điểm SD, hãy tính theo a khoảng cách d từ M đến mặt phẳng (SAC). 

A. $d=\frac{a\sqrt{1513}}{89}$

Đáp án chính xác

B. $d=\frac{a\sqrt{1315}}{89}$

C. $d=\frac{2a\sqrt{1513}}{89}$

Trả lời:

Phương pháp:
– Đổi $d\left(M;\left(SAC\right)\right)$ sang $d\left(H;\left(SAC\right)\right)$
– Trong (ABCD) kẻ $HE\perp AC\left(E\in AC\right),$ trong (SHE) kẻ $HN\perp SE\left(N\in SE\right)$, chứng minh $HN\perp \left(SAC\right)$
– Xác định góc giữa SC và (ABCD), từ đó tính SH.
– Sử dụng $S_{HAC}=\frac{1}{2}HE.AC=\frac{1}{2}{S}_{ABC},$ từ đó tính HE.
– Sử dụng hệ thức lượng trong tam giác vuông tính HN.
Cách giải:

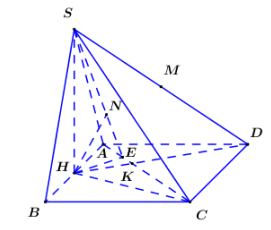
Gọi H là trung điểm AB. Vì $\Delta SAB$ cân tại S nên $SH\perp AB$
Ta có: $\left\{\begin{array}{l}\left(SAB\right)\cap \left(ABCD\right)=AB\\ SH\subset \left(ABCD\right),SH\perp AB\end{array}\right.\Rightarrow SH\perp \left(ABCD\right).$
Gọi $K=HD\cap AC.$ Áp dụng định lí Ta-lét ta có: $\frac{DK}{HK}=\frac{DC}{AH}=2\Rightarrow DK=2HK.$
Ta có $MD\cap \left(SAC\right)=S\Rightarrow \frac{d\left(M;\left(SAC\right)\right)}{d\left(D;\left(SAC\right)\right)}=\frac{SM}{SD}=\frac{1}{2}$
$\Rightarrow d\left(M;\left(SAC\right)\right)=\frac{1}{2}d\left(D;\left(SAC\right)\right)$.
Lại có $DH\cap \left(SAC\right)=K$ nên $\frac{d\left(D;\left(SAC\right)\right)}{d\left(H;\left(SAC\right)\right)}=\frac{DK}{HK}=2\Rightarrow d\left(D;\left(SAC\right)\right)=2d\left(H;\left(SAC\right)\right)$.
Do đó $d\left(M;\left(SAC\right)\right)=d\left(H;\left(SAC\right)\right)$.
Trong (ABCD) kẻ $HE\perp AC\left(E\in AC\right)$, trong (SHE) kẻ $HN\perp SE\left(N\in SE\right)$ ta có:
$\left\{\begin{array}{l}AC\perp HE\\ AC\perp SH\end{array}\right.\Rightarrow AC\perp \left(SHE\right)\Rightarrow AC\perp HN$
$\left\{\begin{array}{l}HN\perp SE\\ HN\perp AC\end{array}\right.\Rightarrow HN\perp \left(SAC\right)\Rightarrow d\left(H;\left(SAC\right)\right)=HN$
 
Vì $SH\perp \left(ABCD\right)$ nên HC là hình chiếu vuông góc của SC lên (ABCD).
$\Rightarrow \angle \left(SC;\left(ABCD\right)\right)=\angle \left(SC;HC\right)=\angle SCH={45}^0$.
$\Rightarrow \Delta SHC$ vuông tại $H\Rightarrow SH=HC=\sqrt{B{C}^2+B{H}^2}=\sqrt{{\left(2a\right)}^2+{\left(\frac{a}{2}\right)}^2}=\frac{a\sqrt{17}}{2}$
Ta có: $S_{HAC}=\frac{1}{2}HE.AC=\frac{1}{2}{S}_{ABC}$
$\Rightarrow HE.AC=\frac{1}{2}.AB.BC$
$\Rightarrow HE=\frac{\frac{1}{2}.AB.BC}{AC}=\frac{\frac{1}{2}.a.2a}{\sqrt{a^2+{\left(2a\right)}^2}}=\frac{a}{\sqrt{5}}$
 
Áp dụng hệ thức lượng trong tam giác vuông SHE ta có:
Nên $HN=\frac{SH.HE}{\sqrt{S{H}^2+H{E}^2}}=\frac{\frac{a\sqrt{17}}{2}.\frac{a}{\sqrt{5}}}{\sqrt{\frac{17a^2}{4}+\frac{a^2}{5}}}=\frac{a\sqrt{1513}}{89}$.
Vậy $d\left(M;\left(SAC\right)\right)=\frac{a\sqrt{1513}}{89}.$
Chọn A.

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Cho a,b,c>0;a≠1,b≠1. Trong các khẳng định sau, khẳng định nào sai? 
   
   

   Câu hỏi:
   

   Cho $a,b,c>0;a\ne 1,b\ne 1.$ Trong các khẳng định sau, khẳng định nào sai? 

   A. ${\log }_{a^c}b=c{\log }_{a}b$

   Đáp án chính xác

   B. ${\log }_{a}b.{\log }_{b}c={\log }_{a}c.$

   C. ${\log }_a\left(bc\right)={\log }_{a}b+{\log }_{a}c$

   D. ${\log }_{a}b=\frac{1}{{\log }_{b}a}$

   Trả lời:

   Phương pháp:
   Sử dụng các công thức logarit.
   Cách giải:
   Ta có ${\log }_{a^c}b=\frac{1}{c}{\log }_{a}b$ nên đáp án A sai.
   Chọn A.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Cho hàm số y=x4−2×2+3. Khẳng định nào sau đây là đúng? 
   
   

   Câu hỏi:
   

   Cho hàm số $y=x^4-2x^2+3.$ Khẳng định nào sau đây là đúng? 

   A. Hàm số chỉ có đúng hai điểm cực trị.         

   B. Hàm số không có cực trị. 

   C. Hàm số có ba điểm cực trị                          

   Đáp án chính xác

   D. Hàm số chỉ có đúng một điểm cực trị.

   Trả lời:

   Phương pháp:
   – Tìm đạo hàm của hàm số.
   – Tìm nghiệm phương trình y’ = 0.
   Cách giải:
   Ta có $y=x^4-2x^2+3\Rightarrow y‘=4x^3-4x=0\iff \left[\begin{array}{l}x=0\\ x=1\\ x=-1\end{array}\right..$
   Vậy hàm số đã cho có 3 điểm cực trị.
   Chọn C.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Cho ∫01fxdx=2 và ∫01gxdx=5. Khi đó ∫01fx−2gxdx bằng 
   
   

   Câu hỏi:
   

   Cho $\underset{0}{\overset{1}{\int }}f\left(x\right)dx=2$ và $\underset{0}{\overset{1}{\int }}g\left(x\right)dx=5.$ Khi đó $\underset{0}{\overset{1}{\int }}\left[f\left(x\right)-2g\left(x\right)\right]dx$ bằng 

   A. 12

   B. -3

   C. 1

   D. -8

   Đáp án chính xác

   Trả lời:

   Phương pháp:
   Sử dụng tính chất tích phân: $\underset{a}{\overset{b}{\int }}\left[f\left(x\right)+g\left(x\right)\right]dx=\underset{a}{\overset{b}{\int }}f\left(x\right)dx+\underset{a}{\overset{b}{\int }}g\left(x\right)dx,\underset{a}{\overset{b}{\int }}kf\left(x\right)dx=k\underset{a}{\overset{b}{\int }}f\left(x\right)dx.$
   Cách giải:
   Ta có $T=\underset{0}{\overset{1}{\int }}\left[f\left(x\right)-2g\left(x\right)\right]dx=\underset{0}{\overset{1}{\int }}f\left(x\right)dx-2\underset{0}{\overset{1}{\int }}g\left(x\right)dx=2-2.5=-8.$
   Chọn D.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Tập hợp T gồm 7 phần tử khác nhau. Số tập con có 3 phần tử của tập hợp T là
   
   

   Câu hỏi:
   

   Tập hợp T gồm 7 phần tử khác nhau. Số tập con có 3 phần tử của tập hợp T là

   A. $\frac{7!}{3!}$

   B. $A_7^3$

   C. 21

   D. $C_7^3$

   Đáp án chính xác

   Trả lời:

   Phương pháp:
   Áp dụng công thức tính tổ hợp.
   Cách giải:
   Số tập con có 3 phần tử của tập hợp 7 phần tử là $C_7^3.$
   Chọn D.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Tập hợp T gồm 7 phần tử khác nhau. Số tập con có 3 phần tử của tập hợp T là
   
   

   Câu hỏi:
   

   Tập hợp T gồm 7 phần tử khác nhau. Số tập con có 3 phần tử của tập hợp T là

   A. $\frac{7!}{3!}$

   B. $A_7^3$

   C. 21

   D. $C_7^3$

   Đáp án chính xác

   Trả lời:

   Phương pháp:
   Áp dụng công thức tính tổ hợp.
   Cách giải:
   Số tập con có 3 phần tử của tập hợp 7 phần tử là $C_7^3.$
   Chọn D.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====