Tìm các giá trị thực của tham số m sao cho điểm cực tiểu của đồ thị hàm số y=x3+x2+mx−1  nằm bên phải trục tung.

Câu hỏi:

Tìm các giá trị thực của tham số m sao cho điểm cực tiểu của đồ thị hàm số $y=x^3+x^2+mx-1$  nằm bên phải trục tung.

A. $m<0$

Đáp án chính xác

B. $0<m<\frac{1}{3}$

C. $m<\frac{1}{3}$

D. Không tồn tại.

Trả lời:

Hướng dẫn giải
Ta có: $y^{‘}=3x^2+2x+m$ .
Đồ thị hàm số có điểm cực tiểu khi phương trình $y^{‘}=0$  có hai nghiệm phân biệt $\iff {\Delta }^{‘}=1-3m>0\iff m<\frac{1}{3}\left(1\right).$
Khi đó, giả sử $x_1$ , $x_2$ (với $x_1<x_2$ ) là hai nghiệm của phương trình  $y^{‘}=0$thì$\left\{\begin{array}{l}{x}_1+x_2=-\frac{2}{3}\\ x_1.x_2=\frac{m}{3}\end{array}\right..$

Bảng biến thiên

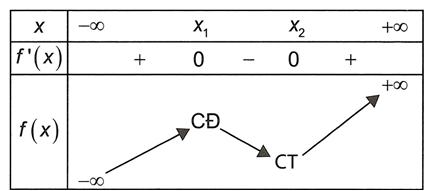
Do $x_1+x_2=-\frac{2}{3}<0$ nên điểm cực tiểu của đồ thị hàm số $y=x^3+x^2+mx-1$  nằm bên phải trục tung $\iff x_1.x_2<0\iff \frac{m}{3}<0\iff m<0$ (2) .
Từ (1), (2) ta có $m<0$
Chọn A. 

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Số cực trị của hàm số fx=x+1x−1  là
   
   

   Câu hỏi:
   

   Số cực trị của hàm số $f\left(x\right)=\frac{x+1}{x-1}$  là

   A. 1

   B. 3

   C. 2

   D. 0

   Đáp án chính xác

   Trả lời:

   Hướng dẫn giải
   Hàm số đã cho xác định trên $ℝ\backslash \left\{1\right\}$
   Ta có: $f^{‘}\left(x\right)=\frac{-2}{{\left(x-1\right)}^2}<0,\forall x\in ℝ\backslash \left\{1\right\}$  . Vậy hàm số không có cực trị.
   Chọn D.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Giá trị cực tiểu của hàm số  fx=−x2+2x+7×2+x+1  là
   
   

   Câu hỏi:
   

   Giá trị cực tiểu của hàm số $f\left(x\right)=\frac{-x^2+2x+7}{x^2+x+1}$ là

   A. $x=-5.$

   B. $y=-\frac{4}{3}.$

   Đáp án chính xác

   C. $x=-\frac{1}{3}.$

   D. $y=8.$

   Trả lời:

   Hàm số đã cho xác định trên R
   Ta có: $f^{‘}\left(x\right)=\frac{-3x^2-16x-5}{{\left(x^2+x+1\right)}^2}.$
   Từ đó: $f^{‘}\left(x\right)=0\iff \left[\begin{array}{l}x=-\frac{1}{3}\\ x=-5\end{array}\right..$
   Bảng xét dấu đạo hàm:
   
   Vậy hàm số đạt cực tiểu tại điểm $x=-5,y_{CT}=f\left(-5\right)=-\frac{4}{3}.$
   Chọn B

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Số cực trị của hàm số fx=x3−3x+23  là
   
   

   Câu hỏi:
   

   Số cực trị của hàm số $f\left(x\right)=x^3-3x+23$  là

   A. 2

   Đáp án chính xác

   B. 1

   C. 3

   D. 0

   Trả lời:

   Hướng dẫn giải
   Hàm số đã cho xác định trên
   Ta có: $f^{‘}\left(x\right)=\frac{x^2-1}{{\left(x^3-3x+2\right)}^2}.$
   Từ đó: $f^{‘}\left(x\right)=0\iff \left[\begin{array}{l}{x}^2-1=0\\ x^3-3x+2\ne 0\end{array}\right.\iff \left\{\begin{array}{l}\left[\begin{array}{l}x=1\\ x=-1\end{array}\right.\\ \left\{\begin{array}{l}x\ne 1\\ x\ne -2\end{array}\right.\end{array}\right.\iff x=-1$
   ( $f^{‘}\left(x\right)$ không xác định tại điểm $x=1$và  $x=-2$).
   Bảng biến thiên:
   
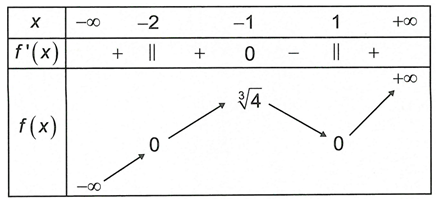
   Vậy hàm số có hai cực trị là $f\left(-1\right)=43$  và $f\left(1\right)=0.$
   Chọn A.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Giá trị cực đại của hàm sốfx=x−2×2+1  là số nào dưới đây?
   
   

   Câu hỏi:
   

   Giá trị cực đại của hàm số$f\left(x\right)=x-2\sqrt{x^2+1}$  là số nào dưới đây?

   A. $\frac{\sqrt{3}}{3}.$

   B. $\sqrt{3}.$

   C. $–\sqrt{3}.$

   Đáp án chính xác

   D. $-\frac{\sqrt{3}}{3}.$

   Trả lời:

   Hướng dẫn giải
   Hàm số đã cho xác định trên
   Ta có: $f^{‘}\left(x\right)=1-\frac{2x}{\sqrt{x^2+1}}.$
   Từ đó: $f^{‘}\left(x\right)=0\iff \sqrt{x^2+1}=2x\iff \left\{\begin{array}{l}2x\ge 0\\ x^2+1=4x^2\end{array}\right.\iff x=\frac{\sqrt{3}}{3}.$
   Bảng biến thiên:
   
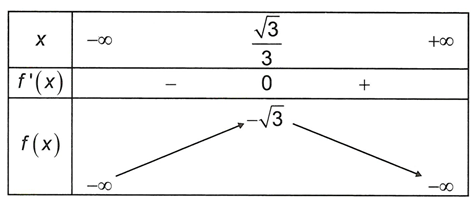
   Vậy hàm số đạt cực đại tại điểm $x=\frac{\sqrt{3}}{3}$, giá trị cực đại của hàm số là $f\left(\frac{\sqrt{3}}{3}\right)=-\sqrt{3}.$
   Chọn C.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Các điểm cực đại của hàm số fx=x−2sinx  có dạng (với k∈ℤ )
   
   

   Câu hỏi:
   

   Các điểm cực đại của hàm số $f\left(x\right)=x-2\sin x$  có dạng (với $k\in \mathbb{Z}$ )

   A. $x=-\frac{\pi }{3}+k2\pi .$

   Đáp án chính xác

   B. $x=\frac{\pi }{3}+k2\pi .$

   C. $x=-\frac{\pi }{6}+k2\pi .$

   D. $x=\frac{\pi }{6}+k2\pi .$

   Trả lời:

   Hướng dẫn giải
   Hàm số đã cho xác định trên R
   Ta có: $f^{‘}\left(x\right)=1-2\mathrm{cosx}$ . Khi đó $f^{‘}\left(x\right)=0\iff \mathrm{cosx}=\frac{1}{2}\iff x=\pm \frac{\pi }{3}+k2\pi ,\left(k\in \mathbb{Z}\right)$
   ${f^{‘}}^{‘}\left(x\right)=2\sin x$

   Vì ${f^{‘}}^{‘}\left(\frac{\pi }{3}+k2\pi \right)=2\sin \left(\frac{\pi }{3}+k2\pi \right)=2\sin \frac{\pi }{3}>0$  nên  $x=\frac{\pi }{3}+k2\pi$là điểm cực tiểu.
   Vì nên ${f^{‘}}^{‘}\left(-\frac{\pi }{3}+k2\pi \right)=2\sin \left(-\frac{\pi }{3}+k2\pi \right)=2\sin \left(-\frac{\pi }{3}\right)=-2\sin \frac{\pi }{3}<0$ là $x=-\frac{\pi }{3}+k2\pi$điểm cực đại
   Chọn A.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====